ИЗОПАР А паропроницаемая мембрана/ветрозащита
С наружной стороны материал имеет гладкую водоотталкивающую поверхность, внутренняя сторона — с шероховатой структурой. «ИЗОПАР А» защищает конструкцию здания и утеплитель от ветра и влаги из внешней среды, обеспечивает выветривание водяных паров из утеплителя и предотвращает проникновение конденсата.
Также применяется для защиты слоя теплоизоляции от ветра, влаги и пыли. Благодаря своей структуре обеспечивает выведение водяного пара из утеплителя, препятствует образованию конденсата.
Используется в зданиях любого типа.
СВОЙСТВА:
Не реагирует на воздействие большинства химических веществ.
Сохраняет свои свойства в широком интервале температур: от -55 0С до +130 0С.
ОБЛАСТИ ПРИМЕНЕНИЯ:
Каркасные стены и стены с наружным утеплителем.Вентилируемые фасады.

Утепленная кровля.
Чердачные перекрытия.
ХАРАКТЕРИСТИКИ:
| № |
Наименование показателя |
Норма |
|---|---|---|
| 1 |
Ширина |
1,6 м |
| 2 | Цвет | белый |
| 3 | Площадь |
30, 70 и 80 м3 |
| 4 | Паропроницаемость | отсутствует |
| 5 | Водоупорность |
Не менее 1000 мм. вод. ст. вод. ст.
|
РАЗМЕРЫ И УПАКОВКА:
| Марка | Ширина, м | Площадь, м3 | Форма выпуска |
|---|---|---|---|
|
ИЗОПАР А |
1,6 |
30 |
ролик |
| ИЗОПАР А | 1,6 | 70 | ролик |
| ИЗОПАР А | 1,6 | 80 | ролик |
СОВЕТЫ ПО МОНТАЖУ:
1. Материал «ИЗОПАР A» не должен применяться в качестве основной или временной кровли.
Материал «ИЗОПАР A» не должен применяться в качестве основной или временной кровли.
2. Недопустим монтаж или использование материала при атмосферных осадках без кровельного покрытия.
3. Материал может применяться как подкровельная ветро-влагозащитная мембрана в утепленных кровлях с различными типами покрытий с углом наклона больше 35°. Материал крепится над утеплителем поверх стропил под обрешеткой.
Все, что нужно знать о мембранах и мембранной одежде
Саша и Лариса в куртках Bergans с мембраной Dermizax 20000 mm
Мембраны бывают разными: поровые, беспоровые, волоконные, гибридные и пр… По материалу они бывают: полиуретановые, тетрафторэтиленовые и, опять же, гибридные. Еще они бывают гидрофобными и гидрофильными. А еще они очень разные по показателям водонепроницаемости и паропроницаемости (дышимости). И пусть магическое слово «мембрана» не сбивает вас с толку.
Водонепроницаемость измеряется в мм водяного столба. Например, 20 000 мм. Меньше меня лично не интересует. Больше – очень хорошо.
Паропроницаемость, в просторечии, дышимость. Сразу скажу, что существует множество тестов: одни меряют, насколько мембрана мешает пару выходить — этот показатель, RET (resistance evaporative thermique), будет выражен в цифрах 1, 2,3, 4, и чем больше, тем хуже, другие измеряют количество пара, которое мембрана может пропустить сквозь себя за единицу времени.
Мне понятнее тесты, которые показывают производительность мембраны в граммах, на метр, в сутки. Но там тоже нюансы, «прямая чашка», «перевернутая чашка» – показатели могут отличаться в два раза.
Чаще мы имеем показатели пароприцаемости, выраженной в граммах, на метр квадратный, в сутки. Например, 15-20 000 гр/м2/24 ч. И здесь меня лично меньшие цифры не устраивают. Всякие мембраны типа 5Х5 – это фуфло и, даже 10Х10 — меня мало интересуют.
Частое заблуждение, что мембрана -это такая чудесная штука, которая обеспечивает чудесную дышимость и, столь же чудесную, водонепроницаемость.
Нет. Резина держит больше любой мембраны, а марля дышит лучше.
Ну и отлично, далась нам эта дышимость! Но резиновые ботинки заполнятся потом, вода теплопроводнее воздуха раз в тридцать, вы замерзли.
Тогда, может и черт с ней, с водонепроницаемостью? Ботинки без мембраны дышат лучше, чем с ней. Но ботинки промокнут под дождем или в снегу, вода теплопроводнее воздуха — опять замерзли.
Без противогаза дышать лучше, чем в нем, но для чего-то он нужен…
Если завощить (покрыть воском) марлю, она станет более водонепроницаемой, но потеряет в дышимости, хотя способ древний, известный и логичный. Конечно, марля тут для абсурдности примера. Или, лучше, понаделать дырочек в резине, сапог станет лучше дышать, но вероятнее всего, промокнет.
Снаружи мембраны у нас: ветер, дождь, снег, под мембраной у нас испарения нашего тела, пот.
Если вам одновременно нужно препятствовать проникновению одного и удалению другого, простого решения не найти. Нужен такой материал, который не пропустит воду внутрь, но даст выйти испарению, поту.
В общем, мембрана – это всегда компромисс между водонепроницаемостью и дышимостью. Мембрана – не чудо, не колония наноботов, не УФМС и, даже, не ЖКХ по непущанию воды снаружи и по выводу пота изнутри. Это вопрос давления и температур. Точнее их разницы под мембраной и снаружи. В физике существует процедура продавливания газа через металл. То есть при нужном давлении, наверное, любой материал может стать мембраной.
Параметры внешнего субстрата нам известны, внутреннего – тоже. Температура наружных субстратов и внутренних, и, соответственно, их активность – разные. Одно из основных условий: снаружи мембраны должно быть холоднее, с внутренней стороны, соответственно, теплее.
Остается найти такой материал для мембраны, чтобы в необходимом диапазоне температур минимально препятствовал бы тяге и был бы, при этом, максимально непроницаем для воды.
Чем и занимаются по сей день производители мембран. Практическим путем пришли к тому, что водонепроницаемость более 20 000 мм водяного столба, уже достаточна для большинства случаев.
Теперь – дышимость. С ней труднее. Как я уже говорил, показатели меньше 15-20 000 гр./м/24 ч – мне не интересны. Но опять вылезают нюансы. Показатели могут быть заоблачные, и 40 000 и 70 000 гр./м/24 ч, а вы при этом сухости внутри вдруг не ощущаете.
А все потому, что они, мембраны разные еще и по строению, и я об этом упоминал, помните: поровые, беспоровые, волоконные, гибридные.
Здесь практику нужно понять только одно, паропроницаемость поровых и волоконных мембран, обеспечивается порами. Т.е. микро, а то и наноотверстиями в теле мембраны, которые непроходимы для воды, но проходимы для более активной, нагретой массы ваших испарений. Можно назвать это – сухой тип.
Т.е. микро, а то и наноотверстиями в теле мембраны, которые непроходимы для воды, но проходимы для более активной, нагретой массы ваших испарений. Можно назвать это – сухой тип.
Или же, оная паропроницаемость обеспечена молекулярной структурой беспоровой или же гибридной мембраны. В этом случае пару нужно, для начала, конденсироваться на внутренней поверхности мембраны и только потом разница давлений увлечет это все вовне. В этом случае мы будем ощущать некоторую увлажненность внутри. Это мы назовем – мокрый тип.
Но это все в идеале. В жизни все очень зависит от условий, в которых вы находитесь и от уровня вашей активности, то есть массы производимых испарений. Если снаружи будет слишком тепло, мембрана будет дышать хуже. Если будет слишком холодно, мембрана может замерзнуть, точнее замерзнут ваши испарения на выходе и так же снизят производительность мембраны, вплоть до полной остановки, если речь пойдет об арктических минусах при высокой влажности.
Современные беспоровые, гидрофильные мембраны имеют выдающиеся показатели дышимости, до 70 000 гр./м/24ч, но будут работать в более узком диапазоне температур.
Показатели поровых, поскромнее 16-32 000 гр./м/24ч, но работают в более широком диапазоне.
Мембранные ткани, это не мембрана, это ткани, вовсе не обязательно тканые, соединенные с мембраной. Показатели голой мембраны всегда отличаются от показателей ткани с мембраной. Это зависит от толщины слоя ткани верха, мембраны и толщины слоя подкладки. Эти слои защищают мембрану от повреждений. Чем они мощнее, тем прочнее изделие. Но сами понимаете, это не может не сказаться на способности мембраны «дышать». Цифры, которые я приводил, относятся к показателям ламинатов.
Когда говорят: трехслойная мембрана, это значит, что слой ткани верха, слой мембраны и слой ткани подкладки соединены/ламинированы так, что кажутся одним слоем. Это наиболее предпочтительный, с точки зрения аутдорной эксплуатации вариант. Изделие из такой ткани можно сунуть в воду, вынуть, встряхнуть от воды и, спокойно, надеть на себя.
Изделие из такой ткани можно сунуть в воду, вынуть, встряхнуть от воды и, спокойно, надеть на себя.
Сегодня производители активно экспериментируют с материалом и структурой подкладочного слоя, и это изрядно сказывается на показателях мембранного ламината в целом.
Часто мы видим, что слой подкладки выполнен не в виде ламинированной ткани, а в виде напыления некоей пленки. Так называемый, двух с половиной-слойный ламинат. Это легче, компактней, дешевле, но менее прочно.
Еще бывает так, что подкладка представляет собой не соединенный с остальными двумя слоями, слой сетки – такую конструкцию называют двухслойной, поскольку соединены только два слоя: верх и мембрана. Этот вариант для аутдора не годится, поскольку, во-первых сетка при намокании будет долго сохнуть, во-вторых, в случае отрицательных температур между сеткой подкладки и мембраной будет накапливаться иней, и его будет много и удалить его, не разрушив сетку, станет нетривиальной задачей.
Из основных моментов осталось сказать только, что слой верха тоже влияет на работу ламината. Представляя собой некую толщину, и будучи пропитан водой, он будет препятствием для корректной работы мембраны, поэтому верх ламината пропитывают водоотталкивающими составами еще на фабрике. И не худо было бы проделывать эту процедуру в дальнейшем, по мере того, как вы будете замечать, что капли воды уже не скатываются с вашей куртки, а сразу образуют мокрое пятно.
И пару моментов напоследок:
– надо понимать, что мембрана под водой работать будет почти никак
– в условиях Северного полюса мембранные изделия почти бесполезны. Из-за высокой влажности и низких температур они будут быстро обмерзать с образованием наледи сперва снаружи изделия, затем внутри. Есть, конечно, лайфхак, надеть поверх мембраны тонкий флис, или какой другой легкий слой и обмерзать будет уже он, а мембрана начнет работать.
К слову, на Южном полюсе такой влажности нет, и там вовсю используют мембранные изделия.
Подытоживая: мембраны это не такая чудо штука, которую, если купил, то она будет неслышно дышать за вас так, что все будет сухо и комфортно. Как дома на диване. Но мембраны – это хорошо, а хорошие мембраны позволяют утащить с собой комфорт очень далеко, а плохие мембраны приносят лишь горечь разочарования и облегчение только в кошельке.
Александр Родичев. Трамонтана.
P.S. Стоит отметить, что Саша довольно категоричен в показаниях мембраны, и меньше, чем на 15000-20000 не согласен. Однако, если вам «по грибы» или переждать короткий кусочек непогоды, а не забивать крючья на стене, то 10000/10000 минимально и достаточно. Для примера, если вы наступили коленом в лужу — то создали давление около 8000 мм. Под лямками рюкзака создается примерно такое же давление (еще и длительное по времени) — это самое «тонкое» место в куртке.
5000/5000 и около того, действительно, нерабочая вещь — вы либо промокните снаружи, либо — изнутри. Проще купить проветриваемое пончо.
Проще купить проветриваемое пончо.
Ну и отдельно стоят разные легкоходные вещи. Если вы видите показатели 20000 на 20000 и с весом 200 грамм, то не ждите от нее долговечности и надежности. Берегите ее, не таскайте с рюкзаком по лесу.
И всегда советуйтесь с консультантами — плохого не посоветуют!
Мембранные куртки тут
Брюки тут
Ветро-влагозащитная паропроницаемая мембрана “Изобонд А”
Описание товара:
Изобонд А — ветро-влагозащитная паропроницаемая мембрана предназначен для защиты наружных стен малоэтажных зданий из бруса каркасной, щитовой или комбинированной конструкции от воздействия атмосферной влаги и ветра.
Область применения:
Конструкции стен зданий с наружным утеплителем
- Во всех случаях применения внешней обшивки (вагонка, сайдинг и т.д.) при наружном утеплении стен укладывается с внешней стороны утеплителя под обшивкой здания, способствует выведению влаги из утеплителя.

Конструкции вентилируемых фасадов многоэтажных зданий
- Изобонд А предохраняет утеплитель от ветра, атмосферной влаги и снега, проникающих в вентилируемый зазор под внешнюю обивку. Способствует выведению влаги из утеплителя.
Конструкции утепленной кровли
- Изобонд А может применяться как подкровельная ветро-влагозащитная мембрана в утепленных кровлях с различными типами покрытий с углом наклона больше 35 градусов. Изобонд А крепится над утеплителем поверх стропил под обрешоткой. Служит как дополнительная защита от ветра и для защиты утеплителя и несущих элементов конструкций от подкровельного конденсата. Не допускается монтаж или использование Изобонд А при атмосферных осадках без кровельного покрытия. Не может применяться в качестве основной или временной кровли!
Технические характеристики:
- Плотность, гр/м²: 90
- Состав: полипропилен
- Разрывная нагрузка прод.
 /попер., Н/5см: 177/129
/попер., Н/5см: 177/129 - Паропроницаемость, гр/м2/сут.: >1000
- Водоупорность, мм.вод.ст.: 250
- УФ-стабильность материал, мес.: 3-4
Купить Ветро-влагозащитная паропроницаемая мембрана “Изобонд А” в г. Краснодар.
Купить Ветро-влагозащитная паропроницаемая мембрана “Изобонд А” в г. Краснодар, ул. Уральская, д. 144, офис 313, 3-й этаж. Позвоните нам по телефону +7(861)203-00-23 и мы предложим вам хорошую цену. Нажмите кнопку купить, впишите номер телефона и мы перезвоним с предложением лучшей цены.
Мембранные белки – молекулярная биология клетки
Как мы видели, все антитела имеют схожую структуру и функции; ферменты
структурно разнообразное, но все они имеют каталитическую функцию. Напротив, хотя все мембранные
белки расположены на мембране, в остальном они структурно и функционально
разнообразный. Как мы отмечали в главе 2 и обсуждали в
более подробно в главе 5, каждый биологический
мембрана имеет такую же основную двухслойную структуру фосфолипидов. С каждой мембраной связана
набор мембранных белков, который позволяет мембране выполнять свои отличительные функции
().Набор белков, прикрепленных к
мембрана варьируется в зависимости от типа клетки и субклеточного расположения.
С каждой мембраной связана
набор мембранных белков, который позволяет мембране выполнять свои отличительные функции
().Набор белков, прикрепленных к
мембрана варьируется в зависимости от типа клетки и субклеточного расположения.
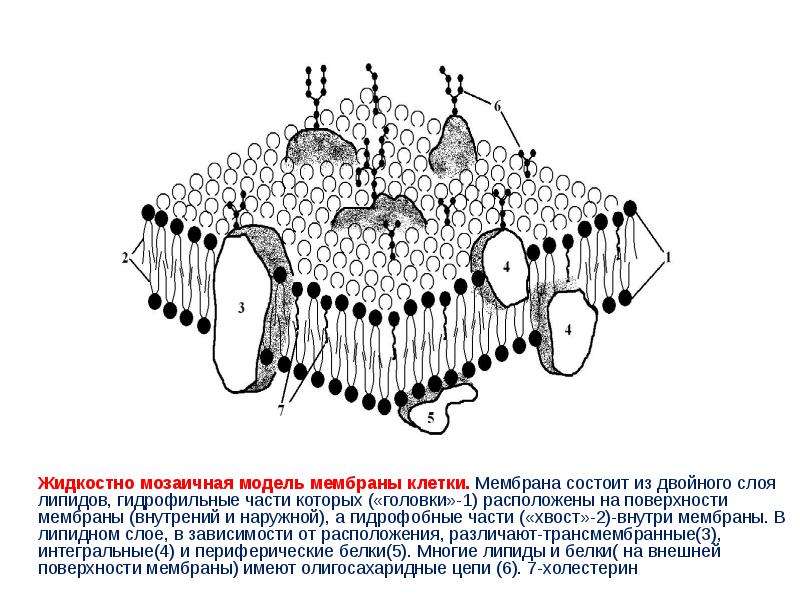
Рисунок 3-32
Схематическая диаграмма типичных мембранных белков в биологической мембране. Фосфолипидный бислой, основная структура всех клеточных мембран, состоит из двух листочки фосфолипидных молекул, жирные ацильные хвосты которых образуют гидрофобную внутреннюю часть the (подробнее …)
Некоторые белки связаны только с поверхностью мембраны, в то время как другие имеют одну скрытую область
внутри мембраны и доменов с одной или обеих сторон от нее.Белковые домены на внеклеточной
Поверхность мембраны обычно участвует в передаче сигналов или взаимодействиях между клетками. Домены внутри
мембрана, особенно те, которые образуют каналы и поры, перемещают молекулы через
мембрана. Домены, расположенные вдоль цитозольной поверхности мембраны, имеют широкий спектр функций,
от закрепления цитоскелетных белков на мембране до запуска внутриклеточной передачи сигналов
пути. Во многих случаях функция мембранного белка и топология его полипептида
цепь в мембране может быть предсказана на основе ее гомологии с другим, хорошо охарактеризованным
белок.В этом разделе мы исследуем характерные структурные особенности мембранных белков.
и некоторые из их основных функций. Более полное описание структуры и функций
различных типов мембранных белков представлена в нескольких последующих главах. Синтез и
процессинг мембранных белков обсуждается в главе
17.
Во многих случаях функция мембранного белка и топология его полипептида
цепь в мембране может быть предсказана на основе ее гомологии с другим, хорошо охарактеризованным
белок.В этом разделе мы исследуем характерные структурные особенности мембранных белков.
и некоторые из их основных функций. Более полное описание структуры и функций
различных типов мембранных белков представлена в нескольких последующих главах. Синтез и
процессинг мембранных белков обсуждается в главе
17.
Белки взаимодействуют с мембранами по-разному.
Мембранные белки можно разделить на две широкие категории – интегральные (внутренние) и периферические (внешние) – в зависимости от характера мембранно-белковых взаимодействий. (видеть ).Большинство биомембран содержат оба типа мембранных белков.
Интегральные мембранные белки, также называемые внутренних белков, имеют один или несколько сегментов, которые встроены в
фосфолипидный бислой. Большинство интегральных белков содержат остатки с гидрофобными боковыми цепями, которые
взаимодействуют с жирными ацильными группами мембранных фосфолипидов, таким образом закрепляя белок на
мембрана. Большинство интегральных белков охватывают весь фосфолипидный бислой. Эти трансмембранные белки также содержат один или несколько трансмембранных доменов.
в виде доменов длиной от четырех до нескольких сотен остатков, простирающихся в водную среду на
с каждой стороны бислоя.Во всех изученных на сегодняшний день трансмембранных белках
Перекрывающие мембрану домены представляют собой α-спирали или несколько β-цепей. Напротив,
некоторые интегральные белки прикреплены к одной из листочков мембраны ковалентно связанными жирными
кислоты, как обсуждается позже. В этих белках связанная жирная кислота встроена в мембрану,
но полипептидная цепь не входит в фосфолипидный бислой.
Большинство интегральных белков охватывают весь фосфолипидный бислой. Эти трансмембранные белки также содержат один или несколько трансмембранных доменов.
в виде доменов длиной от четырех до нескольких сотен остатков, простирающихся в водную среду на
с каждой стороны бислоя.Во всех изученных на сегодняшний день трансмембранных белках
Перекрывающие мембрану домены представляют собой α-спирали или несколько β-цепей. Напротив,
некоторые интегральные белки прикреплены к одной из листочков мембраны ковалентно связанными жирными
кислоты, как обсуждается позже. В этих белках связанная жирная кислота встроена в мембрану,
но полипептидная цепь не входит в фосфолипидный бислой.
Белки периферической мембраны или внешние
белки, не взаимодействуют с гидрофобным ядром фосфолипидного бислоя.Вместо этого они
обычно связаны с мембраной косвенно посредством взаимодействия с интегральными мембранными белками или
непосредственно за счет взаимодействия с полярными головными группами липидов. Периферические белки, локализованные в
цитозольная сторона плазматической мембраны включает белки цитоскелета спектрин и актин в
эритроциты (глава 18) и ферментный белок
киназа С. Этот фермент перемещается между цитозолем и цитозольной стороной плазмы.
мембраны и играет роль в передаче сигнала (Глава 20). Другие периферические белки, включая определенные белки
внеклеточный матрикс, локализуются на внешней (экзоплазматической) поверхности плазмы
мембрана.
Периферические белки, локализованные в
цитозольная сторона плазматической мембраны включает белки цитоскелета спектрин и актин в
эритроциты (глава 18) и ферментный белок
киназа С. Этот фермент перемещается между цитозолем и цитозольной стороной плазмы.
мембраны и играет роль в передаче сигнала (Глава 20). Другие периферические белки, включая определенные белки
внеклеточный матрикс, локализуются на внешней (экзоплазматической) поверхности плазмы
мембрана.
Гидрофобные α-спирали в трансмембранных белках встроены в Бислой
Интегральные белки, содержащие трансмембранные α-спиральные домены, встроены в
мембраны за счет гидрофобных взаимодействий с липидной внутренней частью бислоя и, вероятно, также
за счет ионных взаимодействий с полярными головными группами фосфолипидов. Гликофорин, , основной мембранный белок эритроцитов, проявляет оба типа
взаимодействие. Как показано на фигуре, гликофорин
содержит встроенную в мембрану α-спираль, полностью состоящую из гидрофобных (или незаряженных)
аминокислоты. Прогнозируемой длины этой α-спирали (3,75 нм) достаточно, чтобы
охватывают углеводородное ядро бислоя фосфолипидов. Гидрофобные боковые цепи образуют ван дер
Ваальсово взаимодействие с жирными ацильными цепями и экранирование полярного карбонила (C = O)
и имино (NH) группы пептидной связи, которые все связаны друг с другом водородными связями. Этот
гидрофобная спираль предотвращается от проскальзывания через мембрану фланкирующим набором
положительно заряженные аминокислоты (лизин и аргинин), которые, как считается, взаимодействуют с
отрицательно заряженные головные группы фосфолипидов.В гликофорине большинство этих заряженных остатков лежат
прилегает к цитозольному листку.
Прогнозируемой длины этой α-спирали (3,75 нм) достаточно, чтобы
охватывают углеводородное ядро бислоя фосфолипидов. Гидрофобные боковые цепи образуют ван дер
Ваальсово взаимодействие с жирными ацильными цепями и экранирование полярного карбонила (C = O)
и имино (NH) группы пептидной связи, которые все связаны друг с другом водородными связями. Этот
гидрофобная спираль предотвращается от проскальзывания через мембрану фланкирующим набором
положительно заряженные аминокислоты (лизин и аргинин), которые, как считается, взаимодействуют с
отрицательно заряженные головные группы фосфолипидов.В гликофорине большинство этих заряженных остатков лежат
прилегает к цитозольному листку.
Рисунок 3-33
Аминокислотная последовательность и трансмембранное расположение гликофорина А из плазматическая мембрана эритроцитов. Этот белок является гомодимером, но показана только одна из его полипептидных цепей. Остатки 62–95 погружены в мембрану с последовательностью (подробнее …)
Многие интегральные белки содержат множественные трансмембранные α-спирали
Хотя гликофорин изображен как мономер
с одной α-спиралью, охватывающей бислой, этот белок присутствует в эритроцитах. мембраны в виде димера двух идентичных полипептидных цепей.Две мембранные α
спирали гликофорина, как полагают, образуют спиральную структуру (см.), стабилизированную специфическими взаимодействиями между аминокислотной стороной
цепи на стыке двух спиралей. Сейчас известно, что многие другие трансмембранные
белки содержат две или более мембранных α-спиралей. Например, бактериальный фотосинтетический реакционный центр (PRC) состоит из четырех субъединиц и
несколько простетических групп, в том числе четыре молекулы хлорофилла. В этом сложном белке три
из четырех субъединиц охватывают мембрану; две из этих субъединиц (L и M) содержат по пять
мембранные α-спирали (см.).
мембраны в виде димера двух идентичных полипептидных цепей.Две мембранные α
спирали гликофорина, как полагают, образуют спиральную структуру (см.), стабилизированную специфическими взаимодействиями между аминокислотной стороной
цепи на стыке двух спиралей. Сейчас известно, что многие другие трансмембранные
белки содержат две или более мембранных α-спиралей. Например, бактериальный фотосинтетический реакционный центр (PRC) состоит из четырех субъединиц и
несколько простетических групп, в том числе четыре молекулы хлорофилла. В этом сложном белке три
из четырех субъединиц охватывают мембрану; две из этих субъединиц (L и M) содержат по пять
мембранные α-спирали (см.).
Большое и важное семейство интегральных белков определяется наличием семи
мембранные α-спирали. Более 150 таких «семипролетов».
мембранные белки были идентифицированы. Этот класс интегральных белков типичен: бактериородопсин, белок, обнаруженный в фотосинтезирующих бактериях (). Поглощение света группой сетчатки
прикрепленный к бактериородопсину, вызывает конформационные изменения в белке, что приводит к
перекачка протонов из цитозоля через бактериальную мембрану во внеклеточное пространство. Создаваемый таким образом градиент концентрации протонов через мембрану используется для синтеза АТФ,
как обсуждалось в главе 16. Как общие
расположение семи α-спиралей в бактериородопсине и идентичность большинства
аминокислоты могут быть определены компьютерным анализом микрофотографий двумерных кристаллов.
встроенного в мембрану белка, взятого под разными углами к пучку электронов.
Создаваемый таким образом градиент концентрации протонов через мембрану используется для синтеза АТФ,
как обсуждалось в главе 16. Как общие
расположение семи α-спиралей в бактериородопсине и идентичность большинства
аминокислоты могут быть определены компьютерным анализом микрофотографий двумерных кристаллов.
встроенного в мембрану белка, взятого под разными углами к пучку электронов.
Рисунок 3-34
Общая структура бактериородопсина, определенная с помощью электронографического анализа. двумерных кристаллов белка в бактериальной мембране.Семь соединяющих мембрану α-спиралей обозначены буквами A – G. Сетчатка пигмент ковалентно (подробнее …)
Другие семипространственные мембранные белки включают опсины (белки глаза, поглощающие свет),
рецепторы клеточной поверхности для многих гормонов и рецепторы для пахучих молекул. Аминокислота
Анализ последовательности этих белков показал, что в одном и том же месте не обнаружены аминокислоты.
позиции во всех из них, и только несколько остатков сохраняются даже в значительном количестве
их. Тем не менее, каждый из этих белков содержит семь участков гидрофобных аминокислот.
достаточно длинный (> 22 аминокислот), чтобы покрыть фосфолипидный бислой.Хотя прямые доказательства
отсутствует, считается, что все эти белки принимают конформацию в мембране
аналогичен бактериородопсину. Это один из нескольких примеров того, как следователи могут
предсказывать ориентацию белков в мембране только по аминокислотной последовательности.
Тем не менее, каждый из этих белков содержит семь участков гидрофобных аминокислот.
достаточно длинный (> 22 аминокислот), чтобы покрыть фосфолипидный бислой.Хотя прямые доказательства
отсутствует, считается, что все эти белки принимают конформацию в мембране
аналогичен бактериородопсину. Это один из нескольких примеров того, как следователи могут
предсказывать ориентацию белков в мембране только по аминокислотной последовательности.
Множественные β-тяжи в поринах образуют межмембранное перекрытие «Бочки»
Порины представляют собой класс трансмембранных белков, структура которых отличается
радикально по сравнению с другими интегральными белками.Во внешнем
мембрана грамотрицательных бактерий, таких как E. coli (см.). Наружная мембрана защищает кишечную бактерию от
вредные агенты (например, антибиотики, соли желчных кислот и протеазы), но допускают поглощение и
удаление небольших гидрофильных молекул, включая питательные вещества и продукты жизнедеятельности.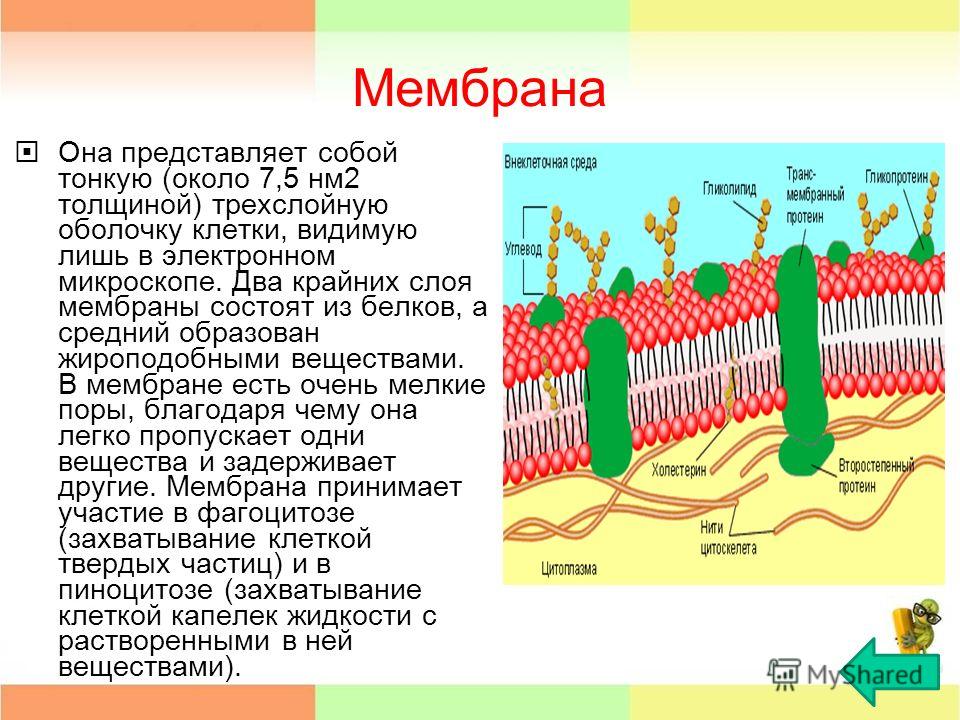 Порины в
внешняя мембрана клетки E. coli обеспечивает каналы для прохождения
дисахариды, фосфаты и подобные молекулы.
Порины в
внешняя мембрана клетки E. coli обеспечивает каналы для прохождения
дисахариды, фосфаты и подобные молекулы.
Аминокислотные последовательности поринов преимущественно полярны и не содержат длинных гидрофобных
сегменты, характерные для интегральных белков, с α-спиральными мембранными доменами.Рентгеновский
Кристаллография показала, что порины представляют собой тримеры идентичных субъединиц. В каждой субъединице 16
β-тяжи образуют бочкообразную структуру с порой в центре (). Как отмечалось ранее, половина аминокислотной стороны
группы β-тяжи указывают в одном направлении, а другая половина – в противоположном
направление (см.). В отличие от типичного шарового
белка, порины имеют расположение наизнанку. В пориновом мономере обращенная наружу сторона
группы на каждой из β-цепей являются гидрофобными и, таким образом, могут взаимодействовать с жирными
ацильные группы липидов мембран или с другими мономерами порина.Боковые группы, обращенные к
внутри мономера порина преимущественно гидрофильны; они выстилают поры, через которые
небольшие водорастворимые молекулы пересекают мембрану.
Рисунок 3-35
Модель трехмерной структуры субъединицы OmpF, порина, обнаруженного в Наружная мембрана E. coli . Все порины являются тримерными трансмембранными белками. Каждый блок имеет бочкообразную форму с β-нити, образующие стенку и трансмембранную пору (подробнее …)
Ковалентно прикрепленные углеводородные цепи закрепляют некоторые белки на мембране
В эукариотических клетках, как отмечалось ранее, полипептидная цепь какой-то целостной мембраны белки не проникают в бислой, а скорее закрепляются в одной створке ковалентно присоединенная углеводородная цепь.На рисунке показаны несколько распространенных липидных якорей.
Рисунок 3-36
Закрепление интегральных белков на плазматической мембране с помощью встроенного в мембрану углеводорода группы (выделены красным). (а) Белок Thy-1 и несколько гидролитических ферментов заякорены гликозилфосфатидилинозитол. Этот комплексный якорь находится только на (подробнее …)
Некоторые поверхностные белки прикреплены к экзоплазматической стороне плазматической мембраны посредством
сложный гликозилированный фосфолипид, связанный с С-концом. Типичный пример этого
тип якоря – гликозилфосфатидилинозитол, который содержит два жирных ацила
группы, N- ацетилглюкозамин, манноза и инозитол (см.). Некоторые ферменты, в том числе щелочная фосфатаза, попадают в
этот класс. Различные эксперименты показали, что фосфолипидный якорь необходим и
достаточно для связывания этих белков клеточной поверхности с мембраной. Например, фермент
фосфолипаза C расщепляет фосфат-глицериновую связь в фосфолипидах, а также в
гликозилфосфатидилинозитол якоря и обработка клеток высвобождением фосфолипазы С.
гликозилфосфатидилинозит-заякоренные белки, такие как белок Thy-1 и щелочная фосфатаза
с поверхности клетки.
Типичный пример этого
тип якоря – гликозилфосфатидилинозитол, который содержит два жирных ацила
группы, N- ацетилглюкозамин, манноза и инозитол (см.). Некоторые ферменты, в том числе щелочная фосфатаза, попадают в
этот класс. Различные эксперименты показали, что фосфолипидный якорь необходим и
достаточно для связывания этих белков клеточной поверхности с мембраной. Например, фермент
фосфолипаза C расщепляет фосфат-глицериновую связь в фосфолипидах, а также в
гликозилфосфатидилинозитол якоря и обработка клеток высвобождением фосфолипазы С.
гликозилфосфатидилинозит-заякоренные белки, такие как белок Thy-1 и щелочная фосфатаза
с поверхности клетки.
Некоторые цитозольные белки прикреплены к цитозольной поверхности мембран с помощью углеводорода.
фрагмент, ковалентно присоединенный к цистеину возле С-конца. Наиболее распространенные якоря:
пренильная, фарнезильная и геранилгеранильная группы. Эти белки подвергаются химической модификации.
в несколько этапов. Во-первых, якорная часть образует тиоэфирную связь с тиоловой группой. цистеина, который находится на четырех остатках от С-конца белка. Модифицированный белок
затем подвергается протеолизу и метилированию; эти реакции удаляют три концевых остатка
и добавить метил к новому С-концу.В некоторых случаях образуются жирные ацилпальмитатные группы
тиоэфир связывается с близлежащими остатками цистеина, обеспечивая дополнительные якоря, которые, как считается,
усиливают прикрепление белка к мембране (см.).
цистеина, который находится на четырех остатках от С-конца белка. Модифицированный белок
затем подвергается протеолизу и метилированию; эти реакции удаляют три концевых остатка
и добавить метил к новому С-концу.В некоторых случаях образуются жирные ацилпальмитатные группы
тиоэфир связывается с близлежащими остатками цистеина, обеспечивая дополнительные якоря, которые, как считается,
усиливают прикрепление белка к мембране (см.).
В другой группе липид-заякоренных цитозольных белков жирная ацильная группа (например, миристат или пальмитат) связан амидной связью с N-концевым остатком глицина (см.). В этих белках N-концевой якорь является необходим для удерживания на мембране и может играть важную роль в связанном с мембраной функция.Например, v-Src, мутантная форма клеточной тирозинкиназы, является онкогенным и может трансформируют клетки только тогда, когда он сохраняет миристилированный N-конец.
Некоторые периферические белки являются растворимыми ферментами, действующими на компоненты мембран
Важной группой белков периферических мембран являются водорастворимые ферменты, которые связывают
с полярными головными группами мембранных фосфолипидов. Одна хорошо изученная группа таких ферментов
представляют собой фосфолипазы , , которые гидролизуют различные связи в головных группах
фосфолипиды ().Эти ферменты обладают
важную роль в деградации поврежденных или старых клеточных мембран.
Одна хорошо изученная группа таких ферментов
представляют собой фосфолипазы , , которые гидролизуют различные связи в головных группах
фосфолипиды ().Эти ферменты обладают
важную роль в деградации поврежденных или старых клеточных мембран.
Рисунок 3-37
Специфичность расщепления фосфолипидов фосфолипазами A 1 , A 2 , C и D. Восприимчивые связи показаны красным. R обозначает полярную группу, присоединенную к фосфату, например, холин в фосфатидилхолине (см. рисунок 5-27a) или инозитол в фосфатидилинозитоле. (подробнее …)
Механизм действия фосфолипазы A 2 иллюстрирует, как такие водорастворимые
ферменты могут обратимо взаимодействовать с мембранами и катализировать реакции на границе раздела
водный раствор и липидная поверхность.Когда этот фермент находится в водном растворе, его
Активный центр, содержащий Ca 2+ , расположен в канале, выстланном гидрофобным
аминокислоты. Связывание фермента с бислоем фосфолипидов вызывает небольшой конформационный
изменение, которое фиксирует белок на головках фосфолипидов и открывает гидрофобную щель.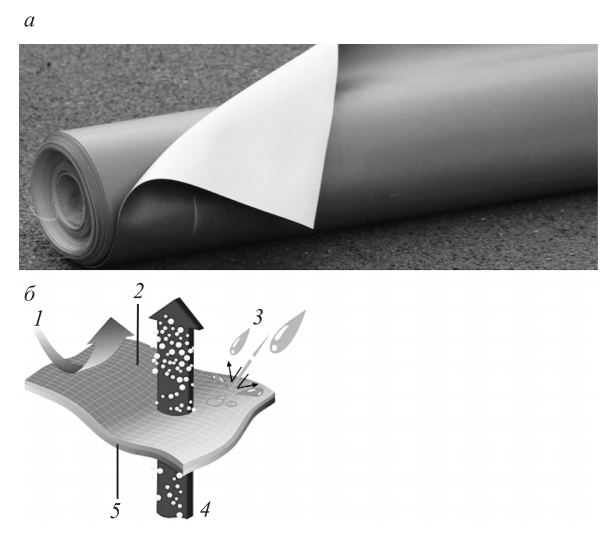 Как
молекула фосфолипида перемещается из бислоя в канал, связанный с ферментом
Ca 2+ связывается с фосфатом в головной группе и позиционирует сложноэфирную связь
расщепляться рядом с каталитическим сайтом.
Как
молекула фосфолипида перемещается из бислоя в канал, связанный с ферментом
Ca 2+ связывается с фосфатом в головной группе и позиционирует сложноэфирную связь
расщепляться рядом с каталитическим сайтом.
РЕЗЮМЕ
- Биологические мембраны обычно содержат как интегральные, так и белки периферической мембраны (см.).
- Интегральные мембранные белки включают трансмембранные белки и липид-заякоренные белки.
- Два типа мембранных доменов обнаружены в трансмембранные белки: одна или несколько α-спиралей или, реже, несколько β-тяжи (как в поринах). Белки, содержащие семь трансмембранных α спирали образуют основной класс, который включает бактериородопсин и многие поверхностные клетки. рецепторы.
- Аминокислотные остатки, модифицированные длинноцепочечными углеводородами к одному мембранному листку прикрепляют некоторые цельные белки (см.).
- Белки периферической мембраны взаимодействуют с интегральной мембраной
белки или с полярными головными группами мембранных фосфолипидов.
 Они не входят в
гидрофобное ядро мембраны.
Они не входят в
гидрофобное ядро мембраны.
Структура и функция белковых комплексов митохондриальной мембраны | BMC Biology
Риццуто Р., Де Стефани Д., Рафаэлло А., Маммукари К.Митохондрии как сенсоры и регуляторы кальциевой сигнализации. Nat Rev Mol Cell Biol. 2012; 13 (9): 566–78.
CAS Статья PubMed Google Scholar
Пеллегрино М.В., Хейнс СМ. Митофагия и митохондриальный развернутый белковый ответ при нейродегенерации и бактериальной инфекции. BMC Biol. 2015; 13:22.
PubMed Central Статья PubMed Google Scholar
Chandel NS. Митохондрии как сигнальные органеллы. BMC Biol. 2014; 12:34.
PubMed Central Статья PubMed Google Scholar
Bratic A, Larsson NG. Роль митохондрий в старении. J Clin Invest. 2013. 123 (3): 951–7.
PubMed Central CAS Статья PubMed Google Scholar

Gray MW, Lang BF, Cedergren R, Golding GB, Lemieux C, Sankoff D, et al.Структура генома и содержание генов в митохондриальной ДНК протистов. Nucleic Acids Res. 1998. 26 (4): 865–78.
PubMed Central CAS Статья PubMed Google Scholar
Amunts A, Brown A, Bai X, Llacer JL, Hussain T., Emsley P, et al. Структура большой рибосомной субъединицы митохондрий дрожжей. Наука. 2014; 343 (6178): 1485–9.
PubMed Central CAS Статья PubMed Google Scholar
Шмидт О., Пфаннер Н., Мейзингер С. Импорт митохондриального белка: от протеомики к функциональным механизмам. Nat Rev Mol Cell Biol. 2010. 11 (9): 655–67.
CAS Статья PubMed Google Scholar
Lackner LL. Формирование динамической митохондриальной сети. BMC Biol. 2014; 12:35.
PubMed Central Статья PubMed Google Scholar

Detmer SA, Chan DC.Функции и нарушения митохондриальной динамики. Nat Rev Mol Cell Biol. 2007. 8 (11): 870–9.
CAS Статья PubMed Google Scholar
Хоппинс С., Лакнер Л., Нуннари Дж. Машины, которые делят и сливают митохондрии. Анну Рев Биохим. 2007. 76: 751–80.
CAS Статья PubMed Google Scholar
Alexandre A, Reynafarje B, Lehninger AL.Стехиометрия векторных движений H +, связанных с транспортом электронов и синтезом АТФ в митохондриях. Proc Natl Acad Sci U S. A. 1978; 75 (11): 5296–300.
PubMed Central CAS Статья PubMed Google Scholar
Meeusen S, McCaffery JM, Nunnari J. Промежуточные звенья слияния митохондрий, обнаруженные in vitro. Наука. 2004; 305: 1747–52.
CAS Статья PubMed Google Scholar

Гутман М., Котляр А.Б., Боровок Н., Нахлиэль Э. Реакция объемных протонов с препаратом внутренней митохондриальной мембраны: измерения с временным разрешением и их анализ. Биохимия. 1993. 32 (12): 2942–6.
CAS Статья PubMed Google Scholar
Перкинс Г.А., Фрей Т.Г. Недавние исследования структуры митохондрий с помощью микроскопии. Микрон. 2000. 31 (1): 97–111.
CAS Статья PubMed Google Scholar
Liao M, Cao E, Julius D, Cheng Y. Структура ионного канала TRPV1, определенная с помощью электронной криомикроскопии. Природа. 2013; 504 (7478): 107–12.
PubMed Central CAS Статья PubMed Google Scholar
Кюльбрандт В. Революция в разрешении. Наука. 2014; 343 (6178): 1443–4.
Артикул PubMed Google Scholar

Дэвис К.М., Штраус М., Даум Б., Киф Дж. Х., Осевач HD, Рыцовска А. и др.Макромолекулярная организация АТФ-синтазы и комплекса I в целых митохондриях. Proc Natl Acad Sci U S. A. 2011; 108 (34): 14121–6.
PubMed Central CAS Статья PubMed Google Scholar
Бхарат Т.А., Дэйви Н.Э., Ульбрих П., Ричес Дж. Д., де Марко А., Румлова М. и др. Структура незрелого ретровирусного капсида при разрешении 8 A с помощью криоэлектронной микроскопии. Природа. 2012. 487 (7407): 385–9.
CAS Статья PubMed Google Scholar
Байрхубер М., Майнс Т., Хабек М., Беккер С., Гиллер К., Виллингер С. и др. Структура человеческого потенциалзависимого анионного канала. Proc Natl Acad Sci U S. A. 2008; 105 (40): 15370–5.
PubMed Central CAS Статья PubMed Google Scholar
Ллопис Дж. , Маккаффери Дж. М., Мияваки А., Фаркуар М. Г., Цзянь Р. Я. Измерение цитозольного, митохондриального и рН Гольджи в отдельных живых клетках с зелеными флуоресцентными белками.Proc Natl Acad Sci U S. A. 1998; 95 (12): 6803–8.
, Маккаффери Дж. М., Мияваки А., Фаркуар М. Г., Цзянь Р. Я. Измерение цитозольного, митохондриального и рН Гольджи в отдельных живых клетках с зелеными флуоресцентными белками.Proc Natl Acad Sci U S. A. 1998; 95 (12): 6803–8.
PubMed Central CAS Статья PubMed Google Scholar
Кукат С., Вурм С.А., Спар Х., Фалькенберг М., Ларссон Н.Г., Якобс С. Микроскопия со сверхвысоким разрешением показывает, что митохондриальные нуклеоиды млекопитающих имеют одинаковый размер и часто содержат единственную копию мтДНК. Proc Natl Acad Sci U S. A. 2011; 108 (33): 13534–9.
PubMed Central CAS Статья PubMed Google Scholar
Kukat C, Davies K, Wurm CA, Spähr H, Bonekamp NA, Kühl I, et al. Перекрестное связывание TFAM с одной молекулой мтДНК образует митохондриальный нуклеоид. Proc Natl Acad Sci U S A. 2015. В печати.
Pfeffer S, Woellhaf MW, Herrmann JM, Forster F. Организация митохондриального механизма трансляции, изученная in situ с помощью криоэлектронной томографии. Nat Commun. 2015; 6: 6019.
Организация митохондриального механизма трансляции, изученная in situ с помощью криоэлектронной томографии. Nat Commun. 2015; 6: 6019.
CAS Статья PubMed Google Scholar
Schleyer M, Neupert W. Транспорт белков в митохондрии: транслокационные промежуточные соединения, охватывающие места контакта между внешней и внутренней мембранами. Клетка. 1985. 43 (1): 339–50.
CAS Статья PubMed Google Scholar
Перкинс Г., Ренкен С., Мартоне М.Э., Янг С.Дж., Эллисман М., Фрей Т. Электронная томография митохондрий нейронов: трехмерная структура и организация крист и мембранных контактов.J. Struct Biol. 1997. 119 (3): 260–72.
CAS Статья PubMed Google Scholar
Голд В.А., Иева Р., Вальтер А., Пфаннер Н., Ван дер Лаан М., Кульбрандт В. Визуализация активных мембранных белковых комплексов с помощью электронной криотомографии.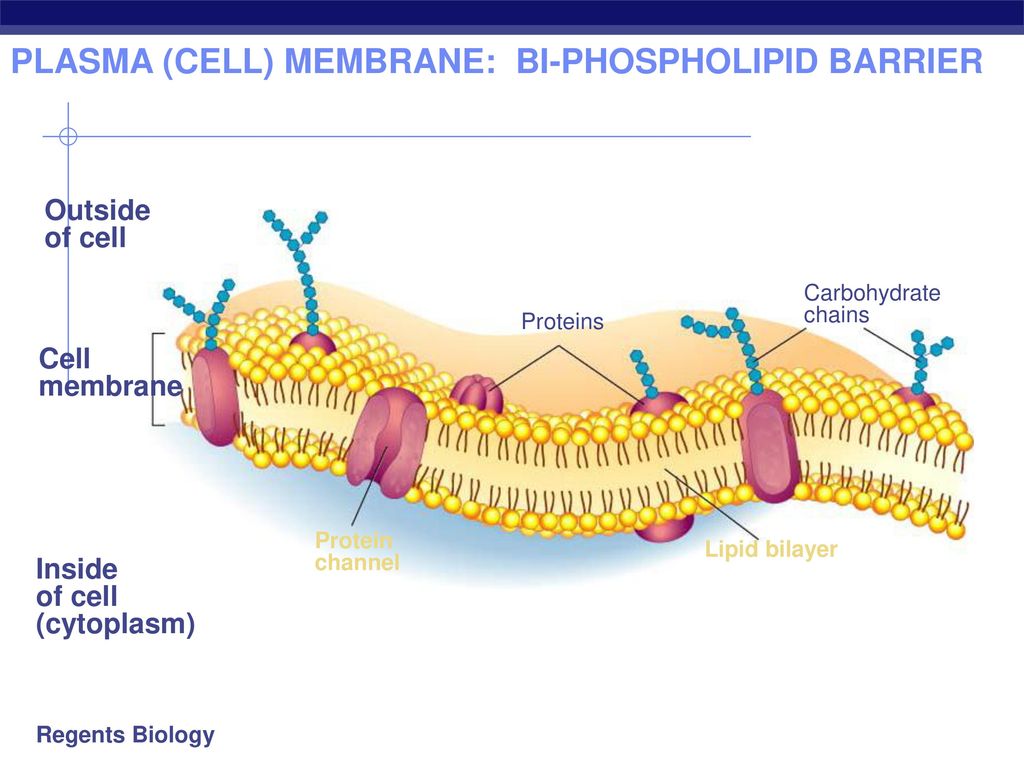 Nat Commun. 2014; 5: 4129.
Nat Commun. 2014; 5: 4129.
PubMed Central CAS Статья PubMed Google Scholar
Pebay-Peyroula E, Dahout-Gonzalez C, Kahn R, Trezeguet V, Lauquin GJ, Brandolin G.Структура митохондриального носителя АДФ / АТФ в комплексе с карбоксиатрактилоидом. Природа. 2003. 426 (6962): 39–44.
CAS Статья PubMed Google Scholar
Sjostrand FS. Электронная микроскопия митохондрий и двойных мембран цитоплазмы. Природа. 1953. 171 (4340): 30–2.
CAS Статья PubMed Google Scholar
Palade GE. Электронно-микроскопическое исследование структуры митохондрий.J Histochem Cytochem. 1953; 1 (4): 188–211.
CAS Статья PubMed Google Scholar
Дэвис К.М., Ансельми С., Виттиг И., Фаральдо-Гомес Дж. Д., Кюльбрандт В. Структура димера дрожжевой F1Fo-АТФ-синтазы и его роль в формировании митохондриальных крист. Proc Natl Acad Sci U S. A. 2012; 109 (34): 13602–7.
Структура димера дрожжевой F1Fo-АТФ-синтазы и его роль в формировании митохондриальных крист. Proc Natl Acad Sci U S. A. 2012; 109 (34): 13602–7.
PubMed Central CAS Статья PubMed Google Scholar
Pfanner N, van der Laan M, Amati P, Capaldi RA, Caudy AA, Chacinska A, et al. Единая номенклатура сайта контакта митохондрий и системы организации крист. J Cell Biol. 2014. 204 (7): 1083–6.
PubMed Central CAS Статья PubMed Google Scholar
von der Malsburg K, Muller JM, Bohnert M, Oeljeklaus S, Kwiatkowska P, Becker T, et al. Двойная роль митофилина в организации митохондриальной мембраны и биогенезе белков.Dev Cell. 2011. 21 (4): 694–707.
Артикул PubMed Google Scholar
Vogel F, Bornhovd C, Neupert W, Reichert AS. Динамическая субкомпартментализация внутренней мембраны митохондрий. J Cell Biol. 2006. 175 (2): 237–47.
J Cell Biol. 2006. 175 (2): 237–47.
PubMed Central CAS Статья PubMed Google Scholar
фон Баллмос С., Виденманн А., Димрот П. Основы синтеза АТФ с помощью АТФ-синтаз F1F0.Анну Рев Биохим. 2009. 78: 649–72.
Артикул Google Scholar
Ватт IN, Монтгомери MG, Рансуик MJ, Leslie AG, Walker JE. Биоэнергетическая стоимость создания молекулы аденозинтрифосфата в митохондриях животных. Proc Natl Acad Sci U S. A. 2010; 107 (39): 16823–7.
PubMed Central CAS Статья PubMed Google Scholar
Stock D, Leslie AGW, Walker JE.Молекулярная архитектура вращательного двигателя в АТФ-синтазе. Наука. 1999; 286: 17701705.
Артикул Google Scholar
Аллен Р.Д., Шредер С.С., Фок АК. Исследование внутренних мембран митохондрий методами быстрого замораживания и глубокого травления. J Cell Biol. 1989. 108 (6): 2233–40.
J Cell Biol. 1989. 108 (6): 2233–40.
CAS Статья PubMed Google Scholar
Strauss M, Hofhaus G, Schroder RR, Kühlbrandt W.Димерные ленты АТФ-синтазы формируют внутреннюю митохондриальную мембрану. EMBO J. 2008; 27 (7): 1154–60.
PubMed Central CAS Статья PubMed Google Scholar
Аллегретти М., Клуш Н., Миллс Д. Д., Вонк Дж., Кюльбрандт В., Дэвис К. М.. Горизонтальные присущие мембране альфа-спирали в а-субъединице статора АТФ-синтазы F-типа. Природа. 2015; 521 (7551): 237–40.
CAS Статья PubMed Google Scholar
Кюльбрандт В., Карен Д. АТФ-синтазы: новый поворот в древней машине. Trends Biochem Sci. 2015. В печати.
Paumard P, Vaillier J, Coulary B., Schaeffer J, Soubannier V, Mueller DM, et al. АТФ-синтаза участвует в формировании морфологии митохондриальных крист. EMBO J. 2002; 21 (3): 221–30.
EMBO J. 2002; 21 (3): 221–30.
PubMed Central CAS Статья PubMed Google Scholar
Bornhövd C, Vogel F, Neupert W, Reichert AS.Потенциал митохондриальной мембраны зависит от олигомерного состояния супракомплексов F1F0-АТФ-синтазы. J Biol Chem. 2006. 281 (20): 13990–8.
Артикул PubMed Google Scholar
Джорджио В., фон Штокум С., Антониэль М., Фаббро А., Фоголари Ф, Форте М. и др. Димеры митохондриальной АТФ-синтазы образуют поры перехода проницаемости. Proc Natl Acad Sci U S. A. 2013; 110 (15): 5887–92.
PubMed Central CAS Статья PubMed Google Scholar
Hunte C, Koepke J, Lange C, Roßmanith T, Michel H. Структура с разрешением 2,3 Å комплекса цитохрома bc1 из дрожжевых Saccharomyces cerevisiae, совместно кристаллизованных с Fv-фрагментом антитела. Структура. 2000. 8: 669–84.
2000. 8: 669–84.
CAS Статья PubMed Google Scholar
Цукихара Т., Аояма Х., Ямасита Э., Томизаки Т., Ямагути Х., Синдзава-Ито К. и др. Вся структура 13-субъединицы окисла цитохром с оксидазы в 2.8 A. Наука. 1996. 272 (5265): 1136–44.
CAS Статья PubMed Google Scholar
Цикерманн В., Вирт С., Насири Х., Зигмунд К., Швальбе Х., Хант С. и др. Механистическое понимание кристаллической структуры митохондриального комплекса I. Наука. 2015; 347 (6217): 44–9.
CAS Статья PubMed Google Scholar
Ефремов Р.Г., Барадаран Р., Сазанов Л.А.Архитектура дыхательного комплекса I. Природа. 2010. 465 (7297): 441–5.
CAS Статья PubMed Google Scholar
Виноткумар К.Р., Чжу Дж., Херст Дж. Архитектура респираторного комплекса млекопитающих I. Природа. 2014. 515 (7525): 80–4.
Природа. 2014. 515 (7525): 80–4.
PubMed Central CAS Статья PubMed Google Scholar
Schägger H, Pfeiffer K. Суперкомплексы в дыхательных цепях митохондрий дрожжей и млекопитающих.EMBO J. 2000; 19 (8): 1777–83.
PubMed Central Статья PubMed Google Scholar
Schäfer E, Seelert H, Reifschneider NH, Krause F, Dencher NA, Vonck J. Архитектура активных суперкомплексов дыхательной цепи млекопитающих. J Biol Chem. 2006. 281 (22): 15370–5.
Артикул PubMed Google Scholar
Альтхофф Т., Миллс Д. Д., Попот Дж. Л., Кюльбрандт В.Расположение компонентов цепи переноса электронов в митохондриальном суперкомплексе крупного рогатого скота I1III2IV1. EMBO J. 2011; 30 (22): 4652–64.
PubMed Central CAS Статья PubMed Google Scholar
Lapuente-Brun E, Moreno-Loshuertos R, Acin-Perez R, Latorre-Pellicer A, Colas C, Balsa E, et al. Сборка суперкомплекса определяет поток электронов в митохондриальной цепи переноса электронов. Наука. 2013; 340 (6140): 1567–70.
CAS Статья PubMed Google Scholar
Mileykovskaya E, Penczek PA, Fang J, Mallampalli VK, Sparagna GC, Dowhan W. Расположение комплексов дыхательной цепи в суперкомплексе Saccharomyces cerevisiae III2IV2, выявленное с помощью криоэлектронной микроскопии одиночных частиц. J Biol Chem. 2012. 287 (27): 23095–103.
PubMed Central CAS Статья PubMed Google Scholar
Блаза Дж. Н., Серрели Р., Джонс А. Дж., Мохаммед К., Херст Дж. Кинетические доказательства против разделения пула убихинона и каталитической значимости суперкомплексов дыхательной цепи. Proc Natl Acad Sci U S. A. 2014; 111 (44): 15735–40.
PubMed Central CAS Статья PubMed Google Scholar

Li P, Nijhawan D., Budihardjo I., Srinivasula SM, Ahmad M, Alnemri ES, et al. Цитохром c и dATP-зависимое образование комплекса Apaf-1 / каспаза-9 запускает каскад апоптотических протеаз.Клетка. 1997. 91 (4): 479–89.
CAS Статья PubMed Google Scholar
Даум Б., Вальтер А., Хорст А., Осиевач HD, Кюльбрандт В. Возрастозависимая диссоциация димеров АТФ-синтазы и потеря крист внутренней мембраны в митохондриях. Proc Natl Acad Sci U S. A. 2013; 110 (38): 15301–6.
PubMed Central CAS Статья PubMed Google Scholar
Наварро А., Боверис А. Система митохондриальной передачи энергии и процесс старения. Am J Physiol Cell Physiol. 2007; 292 (2): C670–86.
CAS Статья PubMed Google Scholar
Dröse S, Brandt U. Молекулярные механизмы производства супероксида дыхательной цепью митохондрий. Adv Exp Med Biol. 2012; 748: 145–69.
Adv Exp Med Biol. 2012; 748: 145–69.
Артикул PubMed Google Scholar
Twig G, Shirihai OS. Взаимодействие митохондриальной динамики и митофагии. Сигнал антиоксидантного окислительно-восстановительного потенциала. 2011. 14 (10): 1939–51.
PubMed Central CAS Статья PubMed Google Scholar
Scheckhuber CQ, Erjavec N, Tinazli A, Hamann A, Nyström T., Osiewacz HD. Уменьшение деления митохондрий приводит к увеличению продолжительности жизни и пригодности двух моделей старения грибов. Nat Cell Biol. 2007. 9 (1): 99–105.
CAS Статья PubMed Google Scholar
Calvo SE, Mootha VK. Митохондриальный протеом и болезнь человека. Анну Рев Геномикс Хум Генет. 2010; 11: 25–44.
PubMed Central CAS Статья PubMed Google Scholar
Хендерсон Р. Возможности и ограничения нейтронов, электронов и рентгеновских лучей для микроскопии с атомным разрешением неокрашенных биологических молекул. Q Rev Biophys. 1995; 28: 171–93.
CAS Статья PubMed Google Scholar
Рис DM, Leslie AG, Walker JE. Структура внешней части мембраны АТФ-синтазы крупного рогатого скота. Proc Natl Acad Sci U S. A. 2009; 106 (51): 21597–601.
PubMed Central CAS Статья PubMed Google Scholar
Symersky J, Pagadala V, Osowski D, Krah A, Meier T., Faraldo-Gomez JD, et al. Структура c (10) кольца митохондриальной АТФ-синтазы дрожжей в открытой конформации. Nat Struct Mol Biol.2012; 19 (5): 485–91. S481.
PubMed Central CAS Статья PubMed Google Scholar
| ||
Альтернативы мембран в мирах без кислорода: создание азотосомы
Реферат
Двухслойная липидная мембрана, которая является основой жизни на Земле, нежизнеспособна вне биологии, основанной на жидкой воде. Этот факт побудил астрономов, которые ищут условия, подходящие для жизни, искать экзопланеты в «обитаемой зоне», узкой полосе, в которой может существовать жидкая вода.Однако могут ли клеточные мембраны быть созданы и функционировать при температурах намного ниже тех, при которых вода является жидкостью? Мы делаем шаг к ответу на этот вопрос, предлагая новый тип мембраны, состоящей из небольших органических соединений азота, способных образовываться и функционировать в жидком метане при криогенных температурах. Используя молекулярное моделирование, мы демонстрируем, что эти мембраны в криогенном растворителе обладают эластичностью, равной эластичности липидных бислоев в воде при комнатной температуре. В качестве доказательства концепции мы также демонстрируем, что стабильные криогенные мембраны могут возникать из соединений, наблюдаемых в атмосфере спутника Сатурна, Титана, известного наличием морей жидкого метана на его поверхности.
Ключевые слова- Титан
- абиогенез
- экзобиология
- липосома
- физическая химия
- квантовая химия
- вычислительная химия
- молекулярная динамика
ВВЕДЕНИЕ
Исследования протобиологии и образования клеток на Земле в основном сосредоточены на нуклеиновых кислотах; действительно, обычно считается, что рибонуклеиновые кислоты были предшественниками земной жизни (гипотеза «мира РНК») ( 1 ).Однако недавние исследования показали, что катализ РНК зависит от установления высоких локальных концентраций, а это означает, что компартментализация, вероятно, была такой же или более ранней фазой, чем РНК ( 2 ). Это подтверждает гипотезу «липидного мира», в которой липидные мембраны сыграли важную роль как очень ранний эволюционный шаг в создании жизни на Земле ( 3 ). Было обнаружено, что липидные бислои без дополнительных клеточных механизмов растут, делятся, способствуют реакциям полимеризации и даже синтезируют РНК из ферментов полимеразы ( 4 – 6 ).
Мембраны земных клеток состоят из бислоя фосфолипидов: поверхностно-активных веществ, состоящих из неполярных липидных цепей и насыщенных кислородом полярных головок. Полярные головки образуют поверхности, совместимые с водой, позволяя мембране разделять водный мир снаружи и водную жизнь внутри. Липидные хвосты фосфолипидов объединяются силами Ван-дер-Ваальса, таким образом стабилизируя мембрану. Везикула, состоящая из такой мембраны, называется липосомой.
Роль самоорганизующихся поверхностно-активных веществ в эволюционной биологии на Земле поднимает вопрос о том, могут ли неводные условия поддерживать какую-либо аналогичную структуру.Экспериментальные исследования были выполнены для создания везикул в неполярных растворителях. Это включало рассмотрение неионных простых эфиров ( 7 ), сложных эфиров ( 8 ), поверхностно-активных веществ ( 9 ) и инвертированных фосфолипидов ( 10 ). Обратные фосфолипидные мембраны даже рассматривались как биологические возможности в жидком метане ( 7 – 16 ).
Жидкий метан представляет особый интерес, потому что это единственная жидкость, кроме воды, которая образует моря на поверхности планетарного тела в нашей солнечной системе.Это тело – спутник Сатурна, Титан ( 11 , 12 ). Неизвестно, сможет ли Титан поддерживать любую форму клеточной мембраны. Однако мы действительно наблюдаем, что на поверхности Титана происходит неизвестный процесс, который потребляет водород, ацетилен и этан, которые постоянно стекают из атмосферы, но не накапливаются ( 13 – 15 ). Это делает жидкий метан очень интересным растворителем для использования в качестве альтернативы клеточной мембране.
Однако фосфолипидные мембраны, которые настолько прочны и эластичны в воде, не работают так хорошо в жидком метане.Неполярные хвосты фосфолипидов, казалось бы, совместимы с неполярным жидким метаном, а полярные головы – друг с другом; Означает ли это, что мембрана, обратная той, которая образовалась в воде, могла существовать в метане? К сожалению нет; эта гипотеза фосфолипидов не учитывает тот факт, что хвосты фосфолипидов представляют собой длинноцепочечные углеводороды, которые будут жесткими при криогенных температурах. Кроме того, атомы фосфолипидного головного компонента, кислорода и фосфора, недоступны ни в какой форме в метановых морях Титана и, вероятно, ни в какой подобной среде жидкого метана.Следовательно, липосомы с обращенной фазой не являются жизнеспособным вариантом. Однако идея использования полярности для предотвращения растворения верна, если существуют какие-либо подходящие материалы.
В качестве доказательства концепции образования пузырьков в среде, богатой метаном, мы начали поиск полярных материалов, используя те, которые образуются естественным образом, когда ультрафиолетовый свет взаимодействует с атмосферой, содержащей метан и азот ( 12 ). Из спектроскопических наблюдений орбитального аппарата «Кассини» мы знаем наиболее распространенные полярные соединения в верхней части метано-азотной атмосферы Титана, как показано в таблице 1 [( 12 ), стр.167]. Ниже в атмосфере все эти виды конденсируются в аэрозоли, препятствуя дальнейшим наблюдениям с помощью Кассини. Лабораторные эксперименты по воспроизведению атмосферы метана и азота обычно дают смолистые остатки молекул, называемые толинами ( 17 ). Было обнаружено, что эти толины состоят из углеводородов, нитрилов и аминов ( 17 ). Поэтому мы также включили в наше исследование первичные нитрилы и амины с длиной пропил-гексила, хотя содержание толинов относительно наблюдаемых Кассини видов остается неопределенным.
Таблица 1 Полярные соединения азота, обнаруженные на Титане, и их содержание в верхних слоях атмосферы, измеренное Кассини [( 12 ), стр. 167].Учитывая проблемы экспериментальных исследований при криогенных температурах, мы приняли подход молекулярного моделирования для отбора наиболее многообещающих кандидатов для самосборки в структуру, напоминающую мембрану. Мы рассматривали только короткие лиганды, учитывая тот факт, что более длинные лиганды не дают преимуществ при таких низких температурах. Все наши молекулы-кандидаты намного короче типичных фосфолипидов, которые включают углеродные цепи длиной от 15 до 20 атомов.Жидкий метан достаточно холоден, чтобы затвердеть практически любое вещество: четырехчленная углеродная цепь, например бутан, намного ниже точки замерзания, равной 133 К в жидком метане. При таких температурах может показаться почти невозможным формирование гибкой органической мембраны, не говоря уже о гибкости, подобной гибкости липидного бислоя. Однако низкая температура также позволяет небольшим молекулам агрегироваться иначе, чем при 300 К. Наша обычная интуиция должна быть приспособлена к более холодному миру.
Мы предположили, что мембраны жидкого метана будут полагаться на полярность азотсодержащих групп («азото»), чтобы удерживать их вместе, точно так же, как земные липосомы полагаются на неполярность алкильных групп. Поэтому мы назвали эти структуры «азотосомами». Сравнение липосом и предлагаемых структур азотосом показано на рис. 1.
рисунок 1 Липосомы и азотосомы.( A ) Липосома в полярном растворителе.Полярные головы скреплены неполярными липидными хвостами. ( B ) Азотосома в неполярном растворителе. Неполярные хвосты подпирают головы, богатые полярным азотом.
Ключевые физические требования к мембране заключаются в том, чтобы она была гибкой и стабильной. Наиболее распространенной мерой гибкости клеточной мембраны является модуль расширения площади K a (также известный как модуль расширения, растяжения или площади сжатия) ( 18 , 19 ). Модуль расширения площади мембран наземных клеток при комнатной температуре равен 0.От 24 до 0,50 Дж / м 2 ( 18 , 19 ). Как мы покажем, некоторые из наших кандидатов на азотосомы лежат в этом диапазоне. Наиболее распространенной мерой стабильности является шкала энергии разложения или времени стабильности ( 20 ). В целом липидные бислои на Земле метастабильны ( 21 ). Мы покажем, что некоторые из наших кандидатов в азотосомы имеют высокую энергию разложения по сравнению с криогенной средой, что приводит к очень длительным временным масштабам стабильности.
Синтез азотосом для экспериментального исследования будет сложным проектом, сродни первому синтезу липосом и дополнительным трудностям в криогенных условиях.Однако молекулы, из которых состоят азотосомы, похожи на молекулы, которые обычно изучаются на Земле, что делает свойства азотосом доступными с помощью стандартного молекулярного моделирования. Молекулярная динамика (МД) десятилетиями использовалась для моделирования двухслойных мембран ( 20 , 22 – 24 ) и полимерных везикул (полимерсомы) ( 25 ). Было обнаружено, что значения K, , и , рассчитанные методом MD, хорошо согласуются с экспериментами ( 18 ), что подтверждает использование нами метода для этих новых мембран.
Чтобы обеспечить молекулярные силы в наших моделированиях, мы использовали Оптимизированные потенциалы для моделирования жидкостей (OPLS), которые являются хорошо известными и эффективными моделями для жидких углеводородов, малых органических молекул ( 26 , 27 ) и полимерсом ( 25 ). Мы подтвердили модели OPLS для наших молекул, подтвердив структуры, генерируемые OPLS, и парные энергии связи по сравнению с квантово-механическими расчетами ( 27 ), как описано в разделе «Материалы и методы».Только молекулы, которые OPLS точно моделировали с точки зрения длин связей, углов и энергий связи, были переданы для изучения в качестве кандидатов на азотосомы.
РЕЗУЛЬТАТЫ
Ошибки в моделях OPLS для длин связей, валентных углов и двугранных (торсионных) углов для тестируемых нами соединений представлены в таблице 2. Расчеты для трех наиболее высоконенасыщенных соединений – цианоацетилена, цианоаллена и 2,4-пентадииннитрила. – не рассматривались далее, потому что их модели OPLS показали ошибки в средней длине облигаций более 0.04 Å, что мы сочли недопустимо большим. Поскольку эти виды крайне ненасыщены, они с наименьшей вероятностью будут стабильными, когда они покинут верхние слои атмосферы, поэтому их непригодность для моделирования OPLS вряд ли будет иметь здесь значение. Для остальных соединений средняя разница между структурами OPLS и ab initio для длин связи составляла 0,008 Å, 0,6 ° в углах и 0,3 ° в диэдрах (если они есть).
Таблица 2 Ошибка в структурах, оптимизированных для OPLS.Средняя разница для каждого вида между его структурой OPLS и структурой, полученной в результате оптимизации ab initio с моделью самосогласованного реакционного поля (SCRF) Онзагера для неявного растворителя.
Ab initio энергии связи были получены в вакууме и в неявном растворителе. Разница между этими энергиями составляла от 0,1 до 1,3 ккал / моль для всех исследуемых веществ, в среднем 0,6 ккал / моль. Разница между энергиями связи OPLS и ab initio составляла от 0,2 до 0,9 ккал / моль, в среднем составляя 0,6 ккал / моль. В целом, значения энергии связи, генерируемой OPLS для данного вида, находятся между значениями ab initio с растворителем и без него, что поддерживает использование моделей OPLS.Можно ожидать, что энергии парной связи OPLS будут находиться между энергиями ab initio в вакууме и ab initio в растворителе, поскольку парные расчеты OPLS «подобны растворителям» из-за неполяризуемости модели OPLS. Это заставляет модель OPLS испытывать частичный эффект растворителя, даже когда присутствует только пара молекул. Особняком среди изученных нами молекул был HCN, энергия связи которого с OPLS была на 1,8 ккал / моль выше значения энергии связи, предсказанного ab initio представлением с неявным растворителем, что позволяет предположить, что модель OPLS для HCN неточна.
Однако, как мы покажем позже, HCN не самособирается в азотосому из-за своего небольшого размера. Таким образом, его чрезмерная энергия связи не будет иметь значения, потому что в дальнейшем он не будет рассматриваться из-за отсутствия самосборки. Энергии связи, найденные тремя методами (расчет OPLS и ab initio для системы в вакууме и растворителе), представлены в таблице 3.
Таблица 3 Парные энергии связи.OPLS и расчеты ab initio дали аналогичные результаты.
Каждая азотосома начинает моделирование как сетку молекул, а затем самоорганизуется в свою предпочтительную структуру.Виды, которые OPLS не мог точно представить, были исключены из рассмотрения, как и HCN, который не образовывал упорядоченный слой, и гексан, который образовывал твердое тело. Модули расширения площади оставшихся азотосом, а также простого бислоя гексана без функциональной головки показаны в таблице 4. Учитывая точность энергий связывания OPLS, мы ожидаем, что эти значения составляют K a и ∆ E с точностью до 20%.
Таблица 4 Гибкость K нитрильных и аминных азотосом и энергия активации Δ E для удаления молекулы из каждой азотосомы.Все наши азотосомы обладают гибкостью, аналогичной гибкости известных мембран наземных клеток: от 0,13 до 0,55 Дж / м 2 для азотосом по сравнению с 0,24 до 0,50 Дж / м 2 для наземных липосом. Что касается тепловых колебаний, азотосомы будут казаться более жесткими, чем земные липосомы, потому что тепловые колебания на Титане меньше, чем на Земле. Однако в отношении механического стресса криогенные азотосомы и липосомы при комнатной температуре будут реагировать на удивление одинаково.
Поучительно сравнение гексана и гексаннитрила. Простой гексан образует слой в восемь раз более жесткий, чем гексаннитрил. Кроме того, бислой гексана является хрупким, как показано на рис. 2. После небольшого растяжения кажется, что он трескается. Напротив, слой гексаннитрила равномерно растягивается на всем протяжении. Единственное различие между этими двумя соединениями состоит в том, что гексаннитрил имеет полярный азотный напор.
Рис. 2 Растяжение азотосомы гексаннитрила и бислоя гексана.Наклон линейной посадки пропорционален модулю площади K a .
Ключевое различие между чистым углеводородным слоем и азотосомой заключается в структуре, обусловленной полярным азотным напором. Мы считаем, что именно эта структура позволяет криогенным азотосомам обладать гибкостью липидного бислоя при комнатной температуре.
Энергетические барьеры диссоциации для каждой азотосомы также приведены в таблице 4. Ацетонитрил, бутаннитрил, гексаннитрил, аминопропан и аминобутан имеют значения Δ E значительно ниже 8 ккал / моль, что указывает на нестабильные азотосомы.Азотосомы пропаннитрила, пентаннитрила, аминопентана и аминогексана имеют энергетический барьер, близкий к 8 ккал / моль. Их следует рассматривать в качестве возможных кандидатов, потому что их значения находятся в пределах 20% неопределенности, которая, как мы считаем, здесь уместна. Азотосомы акрилонитрила демонстрируют высокие барьеры разложения (17 ккал / моль), которые достаточны для обеспечения их стабильности в течение длительного времени.
Геометрия молекулы акрилонитрила, по-видимому, благоприятствует азотосомам и препятствует другим состояниям (рис.3). Это согласуется с тем фактом, что акрилонитрил, как экспериментально известно, имеет несколько неупорядоченную твердую фазу ( 28 ). Как и все изученные здесь азотосомы, азотосомы акрилонитрила симметричны относительно плоскости мембраны, что означает, что, как и липидный бислой, они должны быть способны образовывать везикулы разных размеров.
Рис. 3 Состояния акрилонитрила.( A ) Азотосома. Связанные атомы азота и водорода укрепляют структуру.( B ) Твердый. Соседние атомы азота создают неблагоприятное отталкивание. ( C ) Мицеллы. Соседние атомы азота делают это крайне неблагоприятным. ( D ) Азотосомная везикула диаметром 90 Å, размером с небольшую вирусную частицу.
Расчет свободных энергий, необходимых для определения K a , также позволил нам получить полную свободную энергию разложения для каждой азотосомы. Эти значения показаны в таблице 5. Все эти свободные энергии положительны, что указывает на то, что азотосомное состояние предпочтительнее растворенного состояния.Эти значения свободной энергии зависят от концентрации, поскольку Δ G растворять всегда отрицательно при бесконечном разбавлении. Концентрация, создаваемая растворением одной молекулы азотосомы в каждой коробке, составляет около 0,1%, что выше, чем мы могли ожидать в морях Титана. Однако реальные концентрации в настоящее время неизвестны, поэтому они могут быть или не быть достаточно высокими, чтобы сделать азотосомы термодинамически стабильными. В Δ G нет тенденции в отношении количества атомов углерода в цепи.Δ G , по-видимому, определяется тем, как молекулы подходят друг к другу, а не каким-либо простым свойством самих молекул.
Таблица 5 Свободная энергия Гиббса разложения.Чистая механическая работа, необходимая для удаления молекулы с мембраны, с погрешностью 20%. Эти значения зависят от концентрации.
ОБСУЖДЕНИЕ
Мы предполагаем, что в холодном мире без кислорода пузырьки, необходимые для компартментализации, ключевого требования для жизни, будут сильно отличаться от пузырьков, обнаруженных на Земле.Вместо длинноцепочечных неполярных молекул, образующих прототип земной мембраны в водном растворе, мы находим мембраны, которые образуются в жидком метане при криогенных температурах, благодаря притяжению между полярными головками короткоцепочечных молекул, богатых азотом. Мы назвали такую мембрану азотосомой. Мы обнаружили, что гибкость таких мембран примерно такая же, как у мембран, образованных в водных растворах. Несмотря на огромную разницу в температурах между криогенными азотосомами и земными липосомами при комнатной температуре, которые делают почти любую молекулярную структуру жесткой, они демонстрируют удивительно и захватывающе похожие реакции на механическое воздействие.
На основании наших критериев термодинамической стабильности или, по крайней мере, метастабильности, азотосома кажется реализуемой криогенной мембраной. Исходя из всех известных молекулярных компонентов в атмосфере такого мира, Титана, мы смогли выбрать пару молекул-кандидатов, которые были способны проявлять свойства, которые, по-видимому, важны для образования пузырьков. Например, азотосома акрилонитрила имеет хорошую термодинамическую стабильность, высокий энергетический барьер для разложения и модуль расширения площади, аналогичный таковому у фосфолипидных клеточных мембран в богатых кислородом растворах.Акрилонитрил существует в атмосфере Титана в концентрации 10 частей на миллион и вероятно может образоваться на любом небесном теле с азотно-метановой атмосферой.
Наличие молекул, способных образовывать клеточные мембраны, само по себе не показывает, что жизнь возможна. Тем не менее, он направляет наши поиски на экзотические метаболические и репродуктивные химические процессы, которые были бы аналогичным образом совместимы в криогенных условиях. По мере того, как наше понимание условий, которые могут способствовать развитию внеземной жизни, расширяется, увеличивается и наша вероятность найти ее, возможно, в зоне обитания жидкого метана.
МАТЕРИАЛЫ И МЕТОДЫ
Первым свойством азотосом, которое мы исследовали, была их гибкость, измеренная по модулю расширения площади K a . Одной из процедур, которая использовалась для расчета этого свойства, является моделирование спонтанного колебания площади мембраны в течение длительного прогона МД ( 18 ). Однако этот метод основан на случайной выборке редких событий и, следовательно, имеет проблемы с точностью, завышая оценку K a в ≥2 раз ( 18 ).Вместо этого мы выдавили мембрану на заданную величину и рассчитали модуль расширения площади, исходя из сопротивления растяжению ( 18 ). Это прямо сопоставимо с методом наноиндентирования, который используется для экспериментального нахождения K a , и сравнение такого моделирования и экспериментов с наземными липосомами показало, что они дают эквивалентные результаты ( 18 ).
Вторым критерием, который мы использовали для оценки азотосом, была их стабильность.Одна процедура, которая использовалась для изучения стабильности липосом, состоит в том, чтобы моделировать мембрану в течение длительного периода МД и наблюдать, диссоциирует ли она спонтанно ( 20 ). К сожалению, ожидание диссоциации эффективно только для самых слабых мембран, поскольку МД обычно охватывает только наносекунды моделируемого времени. Лучшая процедура – найти временной масштаб диссоциации по энергии активации ( 29 ). По закону Аррениуса скорость процесса с энергией активации Δ E пропорциональна exp (−Δ E / k B T ), где k B – постоянная Больцмана. и T – абсолютная температура ( 29 ).Если известен временной масштаб процесса без энергетического барьера, t 0 , то временной масштаб процесса с барьером определяется как t = t 0 exp (Δ E / к B T ).
Зависимость шкалы времени от Δ E является экспоненциальной, поэтому неопределенность шкалы времени будет больше, чем основная неопределенность энергетического барьера. К счастью, нам нужен только порядок величины шкалы времени.Для перемещения молекулы на 1 Å при 94 К без энергетического барьера требуется порядка t 0 = 1 пс. Если, например, требуется энергия активации 8 ккал / моль, это дает масштаб времени 1 пс × exp (8 ккал / моль / k B T ) = 235000 с (три земных дня). В отсутствие ошибки модели этот временной масштаб достаточно велик, чтобы можно было предположить, что азотосома достаточно стабильна, если у нее энергетический барьер разложения выше 8 ккал / моль.С погрешностью 20%, соответствующей погрешности между OPLS и ab initio энергиями связывания компонентов азотосом, более консервативным ограничением будет использование барьера в 10 ккал / моль, что соответствует времени разложения более 100 земных лет. .
Проверка силового поля OPLS
Мы подтвердили точность модели OPLS для наших молекул с помощью квантово-механических расчетов. Мы использовали программу квантовой механики Gaussian 09 с алгоритмом оптимизации Берни ( 30 ), используя уровень теории M062X / aug-cc-pVDZ и неявный углеводородный растворитель ( 31 ).Чтобы вычислить энергии связи, мы сравнили энергию оптимизированной свободно плавающей молекулы с энергией оптимизированной пары молекул. Для квантовой энергии связи мы исправили ошибку суперпозиции базисного набора по мере необходимости ( 32 ). Мы подтвердили структуры OPLS и парные энергии связи каждой из изученных здесь молекул в сравнении с этими квантово-механическими расчетами, и мы исключили любые модели OPLS, которые имели ошибки в расстояниях связи более 0,04 Å, в валентных углах (1 °), в двугранных углов (2 °) и энергий связи (1 ккал / моль).Двугранные, которые являются свободными роторами (например, вращение вокруг связи алканов C-C), не были включены в средние ошибки, поскольку их углы не вносят значительного вклада в энергию. Эти данные перечислены в результатах. Мы выполнили эти тесты с использованием ab initio расчетов с вычислительно точным, но особенно точным уровнем теории M062X / aug-cc-pVDZ ( 33 ). Известно, что этот «миннесотский функционал» дает точные парные энергии связи для ван-дер-ваальсовых и полярных систем ( 34 ).
После подтверждения достоверности структур, созданных OPLS, с помощью моделирования ab initio, аналогичным образом были подтверждены и энергии связи. Для сравнения были созданы два набора энергий связи, генерируемых ab initio, один в вакууме и один в неявном растворителе. Энергии на основе растворителей ближе к экспериментальным условиям, тогда как энергии в вакууме использовались, по существу, как границы погрешности. Модели OPLS с ошибками энергии связи в растворителе более 1 ккал / моль были исключены.
MD процедура гибкости мембраны
Чтобы найти гибкость и энергетические барьеры наших кандидатов в азотосомы, нам необходимо вычислить все возможные пути, по которым молекула может покинуть свою азотосому, а затем просуммировать соответствующие свойства этих маршрутов в соответствии с вероятностью их появления. Свойства, которые мы выбрали в качестве релевантных здесь, – это потенциальная энергия и сила, действующая на тестовую молекулу в направлении мембраны. Чтобы подготовить все эти возможные пути, мы начали с репрезентативного участка мембраны, сетки молекул размером 6 × 6 x – y для каждого вида-кандидата.
Затем этот кусок мембраны периодически расширяли, чтобы имитировать двумерную мембрану произвольной длины. Окружающее пространство было заполнено растворителем метаном. Краевые молекулы (те, для которых x = 0 или y = 0) удерживались фиксированными в направлении x , чтобы удерживать мембрану на месте. Мембране давали возможность уравновеситься, чтобы получить желаемую структуру, как показано на рис. 4.
Рис. 4 Положения азотных головок в выбранных азотосомах.( A ) Начальная сетка. ( B ) Аминопентан (аморфный). ( C ) Пентаннитрил (гексагональный). ( D ) Акрилонитрил (гексагональная плотная упаковка).
Затем тестовая молекула (в местоположении x , y = 3,3) постепенно удалялась в направлении z . При каждом приращении тестовой молекуле позволяли свободно перемещаться в направлениях [ x , y ]. В направлении z он был слабо ограничен гармоническим потенциалом, что позволяло ему выбирать близлежащие точки z , но не покидать окрестности.Эта процедура, известная как «зонтичная выборка», позволяет осуществлять выборку всех возможных конфигураций, а также обеспечивает оценку того, была ли выборка адекватной – мы можем просто проверить, достаточно ли у нас выборок из каждого небольшого приращения в направлении z . Схема этого процесса представлена на рис. 5.
Рис. 5 Зонтичный отбор образцов процесса разложения азотосом.Тестовая молекула постепенно отводится от мембраны в направлении z .
Эта процедура необходима из-за высоких барьеров азотосом для разложения. Если бы барьеры для разложения были низкими, система, естественно, произвела бы выборку разложенных состояний в течение смоделированного времени. Зонтичная выборка вынуждает моделирование достичь этих состояний, даже если для их возникновения потребуется очень много времени из-за собственных флуктуаций.
На каждом из миллионов шагов МД оценивалась функция потенциальной энергии и вычислялась сила, необходимая для удержания тестовой молекулы от мембраны.Это дало профили силы и потенциальной энергии в зависимости от расстояния от мембраны, которые приводятся отдельно в дополнительных материалах. Профили силы были интегрированы по расстоянию, чтобы получить профили свободной энергии, как показано на рис. 6. Изменение площади было рассчитано путем измерения отклонения атома азота с выемкой в центре листа и определения площади образованной прямоугольной пирамиды. между ним и удерживаемым атомом азота по углам листа.Эта процедура оказалась очень устойчивой к изменениям общего размера листа. Отклонение зазубренного атома измерялось относительно равновесного состояния мембраны, то есть относительно точки минимума свободной энергии.
Рис. 6 Растяжение азотосом.Наклон аппроксимирующей линии пропорционален модулю площади K a .
Потенциальный энергетический барьер для каждой азотосомы был рассчитан путем обнаружения наибольшего разового непрерывного увеличения потенциальной энергии во время разложения каждой азотосомы.Концепция определяющего скорость энергетического барьера в стиле Аррениуса основана на непрерывности барьера. Если существует устойчивое промежуточное состояние, при котором система может повторно уравновеситься, то это не один барьер, а два меньших барьера с резким увеличением предполагаемой скорости реакции. Поскольку мы использовали зонтичную выборку с ее детальным обзором энергетических профилей, мы смогли разделить их на очень мелкие участки (0,05 Å) и убедиться, что внутри наших барьеров нет промежуточных состояний.Пример барьера (акрилонитрил) показан на рис. 7.
Рис. 7 Профиль потенциальной энергии разложения акрилонитрила.Самый большой мгновенный энергетический барьер – это энергия активации разложения азотосомы.
Некоторые из мелких срезов 0,05 Å, почти все в начале и конце, где не могло произойти перекрытие зонтичного отбора проб, содержали менее 500 образцов. Мы удалили эти участки для рассмотрения как барьеры, потому что (500 образцов) × (2 фс на образец) меньше, чем временной масштаб нашего уравновешивания NPT (1000 фс).В результате наши расчеты энергетического барьера становятся более консервативными, поскольку частота дискретизации участка обратно пропорциональна его энергии.
Все прогоны МД были выполнены с использованием крупномасштабного атомно-молекулярного массивно-параллельного симулятора (LAMMPS; распространение март 2014 г.) ( 35 ). Стандартные параметры OPLS использовались без изменений из наборов данных Jorgensen 2008 ( 36 ). Были соблюдены типичные передовые методы моделирования мембран с помощью МД. Например, ансамбль постоянной температуры и постоянного давления (NPT) применялся с использованием термостата Носа-Гувера и баростата, причем баростат был анизотропным ( 37 ).Анизотропный баростат позволяет мембране свободно изменять или терять свою структуру, повышая реалистичность моделирования ( 20 ). Температура была установлена на 94 К, а давление на 1,45 атм, аналогично условиям на поверхности Титана ( 17 ). Использовалось интегрирование Верле с шагом по времени 2 фс ( 37 ). Алгоритм «частица-частица-сетка» использовался для добавления дальнодействующих кулоновских взаимодействий, которые важны при моделировании мембран ( 38 ).Короткодействующие силы, кулоновские взаимодействия и силы Леннарда-Джонса вычислялись попарно с радиусом отсечки 8 Å ( 38 ). Каждая мембрана была инициализирована как плоская плоскость x – y с периодическими граничными условиями в x , y и z , как показано на рис. 3. Первоначальный размер ячейки моделирования составлял 21 × 21 × 42 Å. Положение тестируемой молекулы изменяли с шагом 0,2 Å, начиная с 2 Å ниже ее начального положения в мембране и заканчивая на 10 Å выше, что дает 60 имитаций для каждого тестируемого вида.Затем сбор данных выполнялся в течение 1 нс на каждом приращении. Направление z на каждую молекулу оказывалось на ее концевой атом азота или, в неполярной молекуле, на ее концевой атом углерода. Это позволяло каждой молекуле вращаться, если она испытывала асимметричную силу, давая ей доступ к максимальному количеству степеней свободы. Ограничения на краевые молекулы были абсолютными ( z силы были установлены равными нулю), тогда как ограничение на тестовую молекулу было наложено как гармоническая сила с жесткостью упругости 10 ккал / моль-Å.Это умеренное ограничение позволило исследуемой молекуле покрыть диапазон 0,2 Å и перекрыться с диапазонами других моделей, обеспечивая непрерывный анализ свойств системы.
Исправление (25 марта 2015 г.): Обновлен раздел благодарностей.
Это статья в открытом доступе, распространяемая на условиях некоммерческой лицензии Creative Commons Attribution, которая разрешает использование, распространение и воспроизведение на любом носителе, при условии, что конечное использование не преследует коммерческих целей и при условии, что оригинальная работа правильно процитировано.
ССЫЛКИ И УКАЗАНИЯ
- ↵
- ↵
- ↵
- ↵
- ↵
- ↵
- ↵
- ↵
- ↵ 90↵110
- 9010 Gffler CA E. Lellouch, TE Cravens, Titan: Interior, Surface, Atmosphere, and Space Environment (Cambridge University Press, Cambridge, UK, 2014), vol. 14.
- ↵
- ↵
- ↵
- ↵
- ↵
- ↵
- ↵
- ↵
- ↵
- ↵10
- ↵
- ↵
- ↵
- ↵
- ↵
- ↵
- ↵
Вт.Йоргенсен, Всеатомные параметры OPLS для органических молекул, ионов, пептидов и нуклеиновых кислот (Йельский университет, Нью-Хейвен, Коннектикут, 2009).
- ↵
- ↵
- Copyright © 2015, Авторы
Электрические свойства клеточных мембран
Фундаментальной единицей всей биологической жизни является клетка, масса которой составляет биомолекулы в водном растворе, окруженные клеточной мембраной . Одна из характерных особенностями живой клетки является то, что она контролирует обмен электрически заряженные ионы через клеточную мембрану и, следовательно, электрический потенциал его внутренней части относительно внешней.Этот Страница Scholarpedia – это базовое введение в механизмы лежащий в основе этого процесса. Хотя большая часть материала относится ко всем биологическим ячеек, мы сосредоточимся на тех механизмах, которые важность для нейронов.
Клетки и клеточные мембраны
Все ячейки окружены ячейкой мембрана. Мы пренебрегаем всеми сложностями обмена веществ и структурный аппарат, находящийся внутри клетки и просто рассматривать его как небольшой мешочек, образованный клеточной мембраной и заполненный с физиологическим раствором (т.е. вода с ионами, растворенными в Это). Точно так же предположим, что внешняя часть камеры представляет собой ванну. физиологического раствора. Это приближение радикально, но вполне разумно, тем более что нас здесь интересуют только основы обработки электрической информации внутри нейрона и между нейронами.
Важнейший элемент (т.е. только , который мы не абстрагировали) прочь!), таким образом, является клеточная мембрана. В простейшем виде это бислой фосфолипидов, т.е.слой, который состоит только из двух фосфолипидов молекулы толщиной. Каждая из этих молекул имеет два конца (один – фосфатная группа, другая углеводородная цепь, то есть липид) и эти два конца имеют очень разные свойства. Фосфатный конец гидрофильный (любит находиться в водной среде и быть окружены молекулами воды). Напротив, липидный конец гидрофобный (он терпеть не может находиться рядом с водой; помните, что масло углеводород!). Люблю и ненавидеть за молекулы означает, что они будут достигают более низкой энергии, если они достигают состояния любви и и способны чтобы избежать ненавистных состояний .Каждая молекула пытается попасть в возможно состояние с самой низкой энергией.
Как можно погрузить молекулу фосфолипида в воду на одном из заканчивается и, в то же время, избегать попадания в воду на другом конце? В Ответ, как это часто бывает, – командная работа! Если достаточно молекул фосфолипидов собираясь вместе, они могут связать свои масляные (углеводородные) концы вместе, образуя двухслойный лист с углеводородными концами в центр, и, в то же время, омыть их фосфатные концы в воде на снаружи листа.Это не работает на границах лист, поэтому лучше всего не иметь концов, т.е. закрывать лист на сам, образуя замкнутую сферу. В результате получается определенный объем вода (или физиологический раствор), окруженная двойным слоем молекул фосфолипидов и – Вуаля! – ячейка ! Фактически, такие искусственных ячеек могут быть изготовлен из входящих в его состав молекул фосфолипидов (для справки см. Scott 1975).
Проводимость
Из упомянутой работы по искусственным мембранам мы знаем, что чистый бислои фосфолипидов – неплохие изоляторы (это не удивительно: нет бесплатных ионы в мембране, поэтому нет носителей для переноса зарядов).{-2} \) (Голдуп и др., 1970).
Проводимость биологических мембран обычно намного выше. на несколько порядков даже в состоянии покоя (т.е. без синаптические влияния и т. д.). Причина в том, что существуют всевозможные ионные каналы и другие поры проникающие мембраны и пропуская дополнительные токи. Это эти токи, которые заставляют клетки вести себя сложным и интересным образом. Мы обсудим некоторые из них ниже.
Емкость
Согласно нашему упрощению, внутри и снаружи клетки представляют собой растворы различных солей в воде.В отличие от клеточной мембраны, соленая вода представляет собой неплохой проводник, потому что есть свободные ионы, которые могут переносить электрические заряды. У нас есть два проводника (внутренний и внешний ячейка), разделенные изолятором (мембраной). Это делает это возможно наличие разного количества электрических зарядов внутри и вне камеры. Если мы можем отделить заряд \ (Q \), применив электрический потенциал \ (V \) через мембрану, мембрана имеет по определению емкость \ (C = Q / V \.{-2} \]
где F – единица измерения емкости («Фарад»).
Удельная емкость биологических мембран очень близка к что получается просто от диэлектрической проницаемости липидов и толщины двухслойный (простой вывод см. в Hobbie, 1997) и, в отличие от проводимости, емкость очень мала. + \), который перемещает два иона калия в клетку и одновременно три натрия ионы из клетки.После того, как этот насос проработает некоторое время, концентрация калия внутри клетки становится больше, чем снаружи, а концентрация натрия снаружи становится больше, чем внутри. Для работы насоса требуется энергия, которая передается насосу в обычной энергетической валюте элемента, т.е. ATP \ (\ rightarrow \) процесс ADP.
Как это создает электрический потенциал? Предположим, мы находимся в термодинамическое равновесие, что в данном контексте означает, что чистая поток ионов исчезает.(Конечно, это динамический равновесие, означающее, что ионы пересекают мембрану в обоих направлений, но в среднем количество ионов, протекающих в ячейке, составляет такое же, как количество ионов, выходящих из ячейки. Следовательно чистый поток , то есть разница между количеством ионов в каждом направлении, равно нулю, но сами числа нет). Тогда вероятность \ (P_ {in} \) найти конкретный ион внутри клетки, по сравнению с вероятностью \ (P_ {out} \) нахождения его снаружи, зависит от энергии ion имеет внутри (\ (E_ {in} \)) vs. снаружи (\ (E_ {out} \)). Из статистической механики мы знаем, что связь между этими вероятностями дается распределением Больцмана:
\ [\ tag {2} \ frac {P_ {in}} {P_ {out}} = \ frac {\ exp (- \ frac {E_ {in}} {kT})} {\ exp (- \ frac {E_ {out}} {kT})} \]
где \ (k \) – постоянная, называемая фактором Больцмана. а \ (T \) – температура (в Кельвинах). Энергия иона, конечно, очень сложная величина, со всеми взаимодействия и биохимические сложности, происходящие в жизни система.К счастью, для наших целей детали не важны: Мы можем переписать ур. (2) в виде
\ [\ tag {3} \ frac {P_ {in}} {P_ {out}} = \ exp \ {- \ frac {E_ {in} -E_ {out}} {kT} \} \]
и мы видим, что только разница энергии считается. Биохимическая среда не очень
разные внутри клетки от вне клетки. Следовательно
химическая энергия ионов внутри и вне клетки примерно равна
то же самое, и единственная реальная разница между энергией ионов
внутри и снаружи находится их электрическая энергия.Это вычислено
непосредственно как \ (zeV \, \), где \ (z \) – валентность
ион, \ (e \) электрический заряд единицы (заряд одной
электрон), а \ (V \) электрический потенциал. Поэтому все
другие энергетические термины отменяются, и мы остаемся с
\ [ \ frac {P_ {in}} {P_ {out}} = \ exp \ {- \ frac {ze (V_ {in} -V_ {out})} {kT} \} \]
Теперь мы можем изменить ситуацию: вместо вычисления вероятностей из напряжений мы можем получить напряжения из вероятностей: Разница напряжений внутри и снаружи ячейки получается как
\ [\ tag {4} \ Delta V = V_ {in} -V_ {out} = \ frac {kT} {ze} \ ln \ frac {P_ {out}} {P_ {in}} \]
Это соотношение известно как уравнение Нернста.Обычно это
выражается через концентрации ионов, но поскольку вероятность
нахождения иона в каком-либо месте пропорционально его
концентрации в этом месте составы эквивалентны. это
также принято устанавливать шкалу напряжения так, чтобы \ (V_ {out} = 0 \) (
выбор электрического «заземления» произвольный; обратите внимание, что это
конвенция изменилась со временем, и в классических работах
Ходжкина и Хаксли, которые цитируются ниже, используется противоположный знак).
Таким образом, мы находим, что каждый вид ионов имеет собственное напряжение, при котором он в статистическом равновесии.Это напряжение обычно называют “обратный потенциал” этого иона, потому что ток, генерируемый эти ионы меняют свой знак, когда это напряжение прикладывается к мембране.
Мембранная накладка в состоянии равновесия
В этом разделе мы рассмотрим участок клеточной мембраны, который может содержат много ионных каналов, но достаточно малы, чтобы трансмембранное напряжение примерно одинаково везде в пластырь. Электрически один единственный ионный канал эквивалентен сопротивление последовательно с источником напряжения: сопротивление \ (r_ {channel} \) – это просто величина, обратная проводимости поры ионного канала (для простоты предположим, что канал проницаема только для одного вида ионов), а напряжение \ (V_i \) – потенциал обращения разновидностей ионов \ (i \), который может проходить через канал.{-1} \), как только что обсуждалось, является суммой проводимости всех каналов, которые позволяют ионам натрия проходить. Согласно закону Ома, ток через эти каналы пропорционален разнице в электрический потенциал (напряжение) на мембране, и Коэффициент пропорциональности – это просто проводимость. Имея в виду наши соглашение о том, что внешнее напряжение равно нулю (земля), ток протекает через мембрану, таким образом \ [\ тег {5} I_ {Na} = \ frac {V_ {Na}} {R_ {Na}} = g_ {Na} V_ {Na} \]
Что делать, если существует более одного типа иона, например.г. натрий и калий? Тогда токи будут течь по обоим типам каналов.
пока не установится равновесие, с напряжением внутри
ячейка где-то между обратными потенциалами этих двух ионов
разновидность. Распространенные названия этого равновесного потенциала – потенциал покоя или потенциал утечки , \ (V_L \. \)
Чтобы вычислить \ (V_L \, \), мы предполагаем, что система уже в равновесии, с внутренней частью ячейки на этом потенциале (что пока неизвестно).{-1} \) – проводимость через калиевые каналы.
Теперь мы можем вычислить \ (V_L \) из требования, чтобы система находится в равновесии. Если это так, то сохранение заряд требует, чтобы все токи нейтрализовали друг друга, или, в другом случае, словами, сумма всех токов равна нулю (это известно как Текущий закон Кирхгофа), таким образом \ (I_ {Na} + I_ {K} = 0 \. \) Вместе с экв. (6) и (7), поэтому имеют \ [\ тег {8} g_ {K} V_ {K} -g_ {K} V_L + g_ {Na} V_ {Na} -g_ {Na} V_L = 0 \]
Единственное неизвестное в этом уравнении – \ (V_L \), и мы можем решить
для получения
\ [\ tag {9} V_L = \ frac {g_ {Na} V_ {Na} + g_ {K} V_ {K}} {g_ {Na} + g_ {K}} \]
Конечно, в это уравнение необходимо вводить напряжения с их
правильные знаки, поскольку они получены из ур.(4). В большинстве
физиологические условия, \ (V_ {Na}> 0 \) и
\ (V_K <0 \. \)
До сих пор мы сосредоточились только на двух видах ионов, натрия и калия, так же, как это сделали Ходжкин и Хаксли, когда они разработали свой знаменитый модель аксона гигантского кальмара (Hodgkin et al, 1952; Hodgkin and Хаксли, 1952a-d). Однако легко увидеть, что уравнение (9) можно обобщить на более двух видов ионов. Тогда потенциал покоя определяется частное двух сумм по всем видам ионов,
\ [ V_L = \ frac {\ sum_i g_ {i} V_ {i}} {\ sum_i g_ {i}} \] где, конечно, \ (V_i \) – потенциал обращения разновидностей ионов \ (i \) а \ (g_i \) – его трансмембранная проводимость.Установлено, что для многих нейронов потенциал покоя близок к \ (- 70 мВ \. \)
Мембранная накладка: временная динамика
Теперь мы готовы выйти за пределы состояния равновесия и рассмотреть поведение клетки при изменении ее трансмембранного напряжения со временем. Чтобы учесть переходные процессы, мы должны учитывать емкость мембраны. Как уже упоминалось, сама мембрана довольно хороший электрический изолятор, что означает, что мы можем накапливать электрические заряды на одна сторона, которая затем не может перейти на другую (конечно, та же самая количество заряда с противоположным знаком будет на другой стороне).Например, если мы поддерживаем внутренний ток \ (I \) для время \ (t \, \) заряд \ (Q = I t \) будет накапливаться внутри. Сохранение заряда требует, чтобы накопление заряда равно току,
\ ( \ frac {dQ} {dt} = я \)
Напряжение в конденсаторе пропорционально его заряду с постоянной пропорциональности – это емкость C. Поскольку C – постоянная величина для идеального конденсатора (и в отличном приближении для клеточной мембраны), мы имеем
\ ( \ frac {dQ} {dt} = C \ frac {dV} {dt} = I \)
Ток \ (I \) в этом уравнении представляет собой сумму ионных токов, которые мы вычислили в уравнениях.(6) и (7)
\ ( I = g_ {Na} (V_ {Na} -V) + g_ {K} (V_ {K} -V) \)
Объединяя два предыдущих уравнения, получаем следующий обыкновенный дифференциал Уравнение для мембранного напряжения:
\ [\ tag {10} C \ frac {dV} {dt} = g_ {Na} (V_ {Na} -V) + g_ {K} (V_ {K} -V) \]
Обратите внимание, что в состоянии равновесия производная по времени исчезает, и мы
снова получим уравнение (8).
Для не зависящих от времени проводимостей (и реверсивных потенциалов) это принято объединять ионные проводимости и напряжения.Действительно, мы можем написать экв. (10) следующим образом:
\ [\ tag {11} C \ frac {dV} {dt} = g_ {Na} V_ {Na} + g_ {K} V_K – (g_ {Na} + g_K) V = ({g_ {Na} + g_K}) \ times (\ frac {g_ {Na} V_ {Na} + g_ {K} V_K} {g_ {Na} + g_K} -V) \]
Использование определения потенциала утечки \ (V_L \) в
экв. (9) и определение проводимости утечки
\ (g_L \) как
\ [\ tag {12} g_L = {g_ {Na} + g_K} \]
мы можем переписать ур. (11) как
\ [\ tag {13} C \ frac {dV} {dt} = g_ {L} (V_ {L} -V) \]
Часто ур.(13) записывается как
\ [\ tag {14}
\ tau \ frac {dV} {dt} = V_ {L} -V
\]
где \ (\ tau = C / g_L \) – постоянная времени ячейки. Из этого
уравнение очевидно, что мембрана приблизится к покоящейся
потенциал \ (V_L \) экспоненциально, с характерным временем \ (\ tau \. \)
До сих пор мы рассматривали только проводимость, не зависящую от напряжения или времени. Есть много других типов проводимости, которые играют роль в нейронах. Один важный класс проводимости является результатом различных типов синапсов, которые отвечают за большинство связи между нейронами.В случае химических синапсов канал закрыт (проводимость g = 0), пока химическое вещество, испускаемое другим нейроном, не заставит канал открыться (проводимость> 0). В в случае электрических синапсов существует фиксированная проводимость между двумя связанными нейронами (проводимость g> 0 всегда) и ток, протекающий между ними, пропорционален разности напряжений в этих двух ячейках (см. уравнение (15) ниже). Другой важный класс проводимости обусловлен открытыми каналами зависимых от напряжения самой ячейки (см. ниже).
Все эти токи имеют ту же форму, что и ток утечки в ур. (13), т.е. все они могут быть записаны как
\ [\ tag {15} г (V_c-V) \]
В этом уравнении \ (V \) – это напряжение исследуемого нейрона, а \ (g \) – проводимость для разновидностей ионов (одного или нескольких), которые переносят ток.
\ (V_c \) – напряжение, специфичное для этого тока; это может быть обратное напряжение
ионы, переносимые проводимостью \ (g \) или, в случае электрического синапса (щелевой переход), это
напряжение внутри партнера
нейрон.Обратите внимание, что как \ (g \), так и \ (V_c \) могут зависеть от времени и других переменных, включая
само трансмембранное напряжение (см. Возбудимость). Например, проводимости типа Ходжкина-Хаксли зависят от
трансмембранное напряжение, и они также имеют свою собственную кинетику открытия и закрытия.
Членов вида (15) может быть много, по одному на каждый ток,
и все добавлены справа
сторона экв. (13)
Взаимодействие в космосе
Мы до сих пор рассматривали электрическую активность в патче мембрана, которая достаточно мала (или достаточно однородна), чтобы вести себя везде одинаково.Многие нейроны достаточно большие (или неоднородные) что их мембраны нельзя описать одной мембраной пластырь. Вместо этого взаимодействие между различными частями клетки мембрану нужно учитывать. Это тема Кабельная теория.
Список литературы
- Голдуп А., Оки С. и Даниелли Дж. Ф. 1970. Последние достижения в науке о поверхности 3: 193
- Хобби Р. К. 1997. Физика среднего уровня для медицины и биологии. 3-е издание.Американский институт физики, Нью-Йорк.
- Ходжкин А. Л., Хаксли А. Ф. и Кац Б. 1952. Измерение вольт-амперных отношений в мембране гигантского аксона Loligo . J. Physiol. 1952. 116: 424.
- Ходжкин, А. Л. и Хаксли, А. Ф. 1952a. Токи, переносимые ионами натрия и калия через мембрану гигантского аксона Loligo . J. Physiol. 116: 449.
- Ходжкин А.Л. и Хаксли А.F. 1952b. Компоненты проводимости мембраны в гигантском аксоне Loligo . J. Physiol. 116: 473.
- Ходжкин А.Л. и Хаксли А.Ф. 1952c. Двойное влияние мембранного потенциала на проводимость натрия в гигантском аксоне Loligo . J. Physiol. 116: 497.
- Ходжкин А.Л. и Хаксли А.Ф. 1952d. Количественное описание мембранного тока и его применение к проводимости и возбуждению в нерве. J. Physiol. 117: 500
- Скотт, А.С., 1975. Электрофизика нервного волокна. Обзоры современной физики 47: 487.
Внутренние ссылки
- Ижикевич Евгений Михайлович (2007) Равновесие. Академия наук, 2 (10): 2014.
Дополнительная литература
- Хобби Р. К. 1997. Физика среднего уровня для медицины и биологии. 3-е издание. Американский институт физики, Нью-Йорк.
- Кох, C. 1999. Биофизика вычислений. Издательство Оксфордского университета, Нью-Йорк-Оксфорд.
Внешние ссылки
См. Также
Электрофизиология, возбудимость, зажим напряжения, теория нейронного кабеля
Клеточная мембрана– обзор
II Бимолекулярная липидная мембрана
Термин плазматическая мембрана происходит от немецкого Plasmamembran, слова, придуманного Карлом Вильгельмом Нэгели (1817–1891) для описания твердой пленки, которая образуется, когда белковый сок поврежденной клетки контактирует с водой.Физиолог Л.В. Хайльбрунн назвал это и подобные явления «реакцией поверхностного осаждения», как описано в его книге The Dynamics of Living Protoplasm (1956). «Протоплазма» – это старый термин для обозначения вещества внутри клеток, который широко использовался до того, как методы электронной микроскопии и дифференциального центрифугирования помогли выяснить подробные структуры и специфические функции отдельных клеточных органелл. Участие того, что мы знаем сегодня как клеточная мембрана, и биохимия образования поверхностной пленки в ответ на повреждение клетки впоследствии не были объяснены.Таким образом, первоначальное использование термина «плазматическая мембрана» имеет неясное отношение к его нынешнему значению.
Многие знания о структуре и функциях мембран получены из исследований красных кровяных телец, как показано на микрофотографии, сделанной с помощью сканирующего электронного микроскопа, на рис. 3.1. Эритроциты высоко дифференцированы и специализируются на транспортировке кислорода и углекислого газа в крови. Они состоят в основном из плазматической мембраны, окружающей концентрированный раствор гемоглобина, и лишены ядра, митохондрий, эндоплазматического ретикулума, рибосом, аппарата Гольджи и лизосом.Более 100 лет назад обширные исследования осмотического давления и проницаемости эритроцитов Гамбургером, растительных клеток де Фриза и многих живых клеток Овертоном предоставили доказательства того, что липоидная мембрана окружает клетки. Жирорастворимые вещества, которые являются липофильными и легко растворяются в липидах, легко проникают в клетки, тогда как водорастворимые вещества поступают в клетки медленнее, если вообще. Овертон обнаружил корреляцию между коэффициентом разделения нефть-вода и проницаемостью мембраны; тем не менее, ни в одном из этих ранних исследований мембрана не постулировалась как отдельная структурная единица для объяснения результатов (см. Jacobs, 1962).
РИСУНОК 3.1. Сканирующая электронная микрофотография эритроцитов человека. Двояковогнутые дискоидные ячейки имеют диаметр 8 мкм, толщину 2,4 мкм по краю и 1,0 мкм в центре.
(от Bessis, M. 1974. Corpuscles. Атлас форм эритроцитов. Springer-Verlag, New York, рис. 1, с разрешения).В 1925 году Гортер и Грендель использовали ацетон для извлечения липидов из известного количества эритроцитов и после испарения растворителя измерили площадь, которую экстрагированные липиды занимали в виде мономолекулярной пленки на границе раздела воздух-вода, с помощью лотка Ленгмюра.По площади пленки экстрагированных липидов и площади поверхности эритроцитов, оцененной с помощью световой микроскопии, они пришли к выводу, что: «Очевидно, что все наши результаты хорошо согласуются с предположением о том, что хромоциты покрыты слоем. жирных веществ толщиной в две молекулы »(Гортер и Грендель, 1925, стр. 443). Однако примерно 40 лет спустя было отмечено, что площадь поверхности эритроцитов на самом деле на 50% больше; Кроме того, после экстракции ацетоном в призраках осталось около 30% липидов.К счастью, эти две ошибки, как правило, уравновешивали друг друга (Bar et al., 1966), показывая, что в редких случаях в науке вы можете быть правы по неправильным причинам. Бимолекулярный липидный листок толщиной 75–100 Å, впервые предложенный Гортером и Гренделем в качестве модели клеточной мембраны (рис. 3.2), до сих пор составляет основу современных представлений о структуре клеточных мембран. Суть этой модели состоит в том, что фосфолипиды мембраны расположены в параллельных слоях, образуя два полуслоя с их полярными головными группами, обращенными к водным внутриклеточным и внеклеточным растворам, а их неполярные цепи жирных кислот взаимодействуют латерально внутри гидрофобного ядра мембраны.
РИСУНОК 3.2. Модель бимолекулярной фосфолипидной мембраны, предложенная Гортером и Гренделем (1925).
Для чистых липидов ожидаемое поверхностное натяжение , измеренное в лотке Ленгмюра, составляет около 9 дин / см, но поверхностное натяжение морских яиц и других типов клеток примерно в 50–100 раз меньше всего при 0,1– 0,2 дин / см. Поверхностное натяжение можно представить как силу, необходимую для закрытия щели на поверхности мембраны. Даниелли и Харви обнаружили, что яичный белок может снизить поверхностное натяжение границы раздела масло-вода примерно до 0.6 дин / см, что привело Дэвсона и Даниелли (1943) к постулированию наличия двух пленок белка, связанных с полярными головными группами на каждой стороне бимолекулярного липидного листка, модель, которая стала известна как пауцимолекулярная мембрана Дэвсона-Даниелли (Рис. 3.3). Предположительно, белок функционировал, чтобы укрепить и стабилизировать тонкую липидную пленку. Paucimolecular означает, что эта модель включала всего несколько молекул: бимолекулярный липидный листок с прилипшими белковыми пленками на внутренней и внешней поверхностях.
РИСУНОК 3.3. Пауцимолекулярная модель структуры мембраны.
(От Даниелли, Дж. Ф. и Дэвсона, HA (1935). Вклад в теорию проницаемости тонких пленок. J Cell Comp Physiol. 5, 495–508, стр. 498, перепечатано с разрешения Wiley-Liss, Inc. , дочерняя компания John Wiley and Sons, Inc.)С помощью электрофизиологических методов было измерено электрическое сопротивление клеточных мембран, которое оказалось очень высоким, что также согласуется с предложением об изоляционной липидной мембране, окружающей клетки.В других исследованиях мембран было определено их двойное лучепреломление . Двулучепреломление – это оптическое свойство некоторых ориентированных материалов, которое можно определить, поместив образец между двумя скрещенными поляроидами на предметном столике микроскопа. Пленка Polaroid пропускает только свет, электрический вектор которого параллелен оси пленки Polaroid; две пленки Polaroid, пересеченные под прямым углом и поднятые к свету, кажутся черными. Но если кристалл или другое вещество, в котором сами молекулы ориентированы, поместить между скрещенными поляроидами, проходящий свет будет поляризован по кругу, и образец будет выглядеть ослепительно ярким.Образец, который кажется ярким при помещении между скрещенными поляроидами, называется двулучепреломляющим. Собственное двойное лучепреломление обусловлено ориентированной природой отдельных молекул, таких как нитчатые белки, тогда как формирует двойное лучепреломление обусловлено ориентированным расположением молекул в массиве, например, при параллельной упаковке актиновых и миозиновых нитей в мышцах. саркомеры. Когда мембраны эритроцитов просматривали с помощью поляризационного микроскопа, липиды вносили вклад в двойное лучепреломление, как и лежащий в основе цитоскелет, в соответствии с паучимолекулярной моделью структуры мембраны.
Электронные микрофотографии с высоким разрешением мембраны блока также подтверждают паучимолекулярную модель Дэвсона – Даниелли. Термин элементарная мембрана относится к повсеместно распространенной триламинарной структуре толщиной 75–100 Å, наблюдаемой на электронных микрофотографиях тонких срезов клеток и органелл. Изображение выглядит как две темные линии, каждая толщиной около 25–30 ÅA, окружающие более светлую зону, и особенно хорошо разрешается в образцах, зафиксированных перманганатом калия. Электронно-микроскопический снимок тонкого среза плазматической мембраны эритроцитов человека показан на рис.3.4. Практически такая же триламинарная структура наблюдалась не только на поверхности эритроцитов, но также и в мышечных клетках, нервных клетках, эпителиальных клетках, растительных клетках, бактериальных клетках и практически во всех исследованных органеллах мембранных клеток. В ситуациях, когда две клетки плотно прилегали друг к другу, две триламинарные структуры составляли двойную мембрану . В миелиновой оболочке, окружающей нервные клетки, была видна серия триламинарных структур в спиральном расположении, согласующемся с оболочкой нервных аксонов мембраной шванновских клеток, как показано на рис.3.5A. Поскольку подробные химические реакции перманганата калия с тканью полностью не изучены, оставалась некоторая неопределенность в отношении основы изображения, которое наблюдалось в шлифах. Повсеместное распространение единичной мембраны, однако, было воспринято как веское свидетельство в поддержку паучимолекулярной модели Дэвсона-Даниелли. Дальнейшие исследования многослойной миелиновой оболочки нервных аксонов с помощью дифракции рентгеновских лучей центрифугированных нефиксированных и неокрашенных мембран дали профили электронной плотности, которые также согласуются с паучимолекулярной моделью Davson-Danielli (Worthington and McIntosh, 1973).Как видно на рис. 3.5B, электронная плотность низкая в гидрофобной сердцевине мембраны и высокая в полярных областях фосфатных групп. Более того, толщина мембраны, определенная из этих вычисленных профилей электронной плотности неокрашенной миелиновой оболочки, количественно согласуется с толщиной мембраны в тонких срезах, фиксированных перманганатом калия – наблюдение, представляющее убедительные доказательства, подтверждающие предложение о бимолекулярном фосфолипиде. листочка как основа структуры клеточных мембран.Таким образом, доказательства для модели пауцимолекулярной мембраны состояли из исследований проницаемости, электрического сопротивления и микроскопических наблюдений двойного лучепреломления с помощью светового микроскопа, а также изображений с высоким разрешением как окрашенных, так и неокрашенных клеток с помощью электронного микроскопа. Эти убедительные аргументы были обобщены в классической монографии под названием The Permeability of Natural Membranes , написанной Дэвсоном и Даниелли (1943), книге, которая сильно повлияла на последующее развитие клеточной и мембранной физиологии.
РИСУНОК 3.4. Электронная микрофотография тонкого среза единичной мембраны эритроцита.
(микрофотография, сделанная Дж. Д. Робертсоном из Дайсона, Р. Д. (1974). Клеточная биология. Молекулярный подход. Аллин и Бэкон, Бостон, с разрешения).РИСУНОК 3.5. (A) Миелиновая оболочка аксона спинного мозга (любезно предоставлена доктором Седриком Рейном). (B) Профиль электронной плотности седалищного нерва лягушки.
(From Worthington, C.R. and McIntosh, T.J. (1973). Прямое определение профиля электронной плотности нервного миелина.Природа – новая биология. 245, 97–99, с. 99. Перепечатано с разрешения Nature , авторское право 1973 Macmillan Magazines Ltd.)Пространственное моделирование интерфейса мембрана-цитозоль в передаче сигнала протеинкиназы
Цитата: Giese W, Milicic G, Schröder A, Klipp E (2018) Пространственное моделирование интерфейса мембрана-цитозоль в передаче сигнала протеинкиназы. PLoS Comput Biol 14 (4): e1006075. https://doi.org/10.1371/journal.pcbi.1006075
Редактор: Йенс Нильсен, Технологический университет Чалмерса, ШВЕЦИЯ
Поступила: 10.10.2017; Одобрена: 7 марта 2018 г .; Опубликовано: 9 апреля 2018 г.
Авторские права: © 2018 Giese et al. Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания автора и источника.
Доступность данных: Все соответствующие данные находятся в документе и его файлах с вспомогательной информацией.
Финансирование: Эта работа была поддержана грантом Немецкого исследовательского фонда (CRC 740 «От молекул к модулям») EK. GM и AS выражают признательность за поддержку исследовательской программе Sparkling Science Федерального министерства науки, исследований и экономики Австрии (BMWFW) в рамках проекта Sparkling Science «EMMA {Эксперименты с математическими алгоритмами}» (SPA 05/172).Финансирующие организации не играли никакой роли в дизайне исследования, сборе и анализе данных, принятии решения о публикации или подготовке рукописи.
Конкурирующие интересы: Авторы заявили, что конкурирующих интересов не существует.
Введение
Клеткам необходимо реагировать на широкий спектр внешних стимулов, таких как изменения окружающей среды или внеклеточные коммуникационные сигналы. Сигналы, передаваемые от рецепторов клеточной поверхности к генам-мишеням в ядре, часто передаются каскадами ковалентных модификаций белков.Эти модификации состоят из взаимопревращаемых форм белка, например, фосфорилированного и нефосфорилированного белка. Сигнальные каскады встречаются во многих различных вариантах, включая каскады митоген-активируемой протеинкиназы (MAPK) и небольшие каскады GTPase.
Механизмы передачи сигналов, осуществляемые сетями белок-белковых взаимодействий, очень модульны, а регуляторное поведение возникает из относительно простых модификаций [1]. Пространственное расположение сигнальных каскадов варьируется в разных биологических системах.Мы фокусируемся на локализации сигнальных компонентов, которые могут быть привязаны к клеточной мембране или свободно диффундировать в цитозоле. Привязка сигнальных молекул к клеточной мембране может быть опосредована модификациями липидирования [2–6], совместной локализацией с помощью мембраносвязанных каркасов [7] или белков, закрепляющих мембраны [8]. Часто первые шаги передачи сигнала происходят на мембране, а затем продолжаются в цитозоле. Мы исследуем каскады линейной передачи сигналов с различными реализациями пространственного расположения компонентов передачи сигналов, как показано на рисунке 1.Здесь мы сосредотачиваемся на интерфейсе мембрана-цитозоль, который включен в сигнальный мотив, показанный на Рис. 1 (B) и 1 (C).
Рис. 1. Пространственная организация сигнальных каскадов.
( A ) Эскиз классической модели передачи временных сигналов. Распространение этой модели на трехмерное пространство естественным образом приводит к появлению множества различных пространственных мотивов. ( B ) Сигнал сначала обрабатывается сигнальными компонентами, привязанными к мембране, а затем передается на границе раздела мембрана-цитозоль в цитозоль.( C ) Компоненты передачи сигналов непосредственно активируются на границе раздела мембрана-цитозоль и диффундируют через цитозоль. Обратите внимание, что коэффициенты диффузии для боковой диффузии вдоль мембраны намного ниже, чем в цитозоле.
https://doi.org/10.1371/journal.pcbi.1006075.g001
Во многих экспериментальных и теоретических исследованиях сигнальных каскадов клетка рассматривается как ряд хорошо перемешанных компартментов без изменений в размере, форме или органеллах. расположение.Попытки количественного описания сигнальных каскадов с акцентом на временные аспекты были сделаны в [9–12]. Однако пространственному описанию сигнальных процессов уделялось меньше внимания, несмотря на его важность для понимания морфологии клеток и регуляции роста во времени и пространстве [13]. Примеры пространственных эффектов в масштабе длины отдельных клеток варьируются от процесса спаривания дрожжей [14, 15] до распространения пространственной информации в нейронах гиппокампа, которая контролируется формой клетки, и наоборот [16, 17].
Поскольку цитозоль масштабируется вместе с объемом клетки, а клеточная мембрана – с площадью поверхности клетки, реакции на мембране и в масштабе цитозоля зависят от отношения поверхности клетки к объему клетки. Например, мы получаем отношение площади к объему ∝ 3/ R ячейка для сферической геометрии ячейки, где R ячейка – это радиус ячейки. Мы покажем, что это масштабирование влияет на общую скорость фосфорилирования сигнальных белков, которые диффундируют в цитоплазматическом объеме, который зависит от размера клетки.В то время как цитозольные градиенты естественным образом возникают от мембраны к ядру, связанные с мембраной компоненты могут образовывать градиенты только вдоль мембраны, что изменяет ответ на гетерогенные сигналы. Более того, диффузия на мембрану для мембраносвязанных компонентов происходит намного медленнее, чем для цитозольных компонентов [18]. Ожидается, что оба эти фактора в значительной степени изменят свойства сигнальной трансдукции пути.
Анализ и сравнение пространственных мотивов передачи сигналов в ответ на пространственно однородные и гетерогенные сигналы представлены в этом исследовании.Естественным продолжением широко распространенных обыкновенных дифференциальных уравнений являются уравнения в частных производных с объемной поверхностью [19, 20]. Здесь основная часть относится к клеточным компартментам, которые представлены как объем, например цитоплазма или ядро, тогда как поверхность относится ко всем клеточным структурам, которые представлены как область, такая как клеточная или ядерная мембрана. С момента своего появления в клеточных сигнальных системах [21] уравнения с частными производными для объемной поверхности успешно применялись в нескольких моделях поляризации клеток [18, 22–24].Однако мембрано-цитозольные интерфейсы на разных стадиях сигнального каскада еще не исследованы.
Мы начинаем с анализа двух различных мотивов с упрощенной линейной кинетикой, которая позволяет разработать точные аналитические решения для стационарного состояния. Оба мотива различаются по зависимости от размера клеток, и мы далее показываем, что их поведение может радикально отличаться от предположения о хорошо смешанных компартментах. Масштабирование передачи сигнала по времени исследуется методом локальных времен накопления [25].Мы продолжаем исследовать реакцию и чувствительность к пространственно неоднородным сигналам, таким как сигнальные градиенты для симметричных и асимметричных форм клеток. В последнем разделе мы продолжаем численные исследования систем с отрицательными обратными связями, которые приводят к колебаниям, зависящим от размера ячейки. Анализ Фурье во времени используется для понимания зависимости частоты и амплитуды колебаний от размера ячейки. В зависимости от пространственного мотива получены пределы размера клетки для подавления колебательного поведения.
Мы начинаем с линейного сигнального каскада с различными локализациями мембранно-цитозольного интерфейса, как показано на рис. 1. Мы используем простую каскадную модель из [9], в которой стимуляция рецептора приводит к последовательной активации нескольких последующих протеинкиназы. Эта модель расширяется в космос следующим образом. Мы предполагаем линейный каскад с компонентами N , где первые компоненты M < N локализованы на мембране, в то время как остальные компоненты N – M предположительно свободно диффундируют в цитозоле.Уравнения для мембраносвязанных компонентов читаются следующим образом: (1) Здесь – локальные концентрации сигнальных молекул на клеточной мембране. Предполагается, что скорость активации первого компонента сигнализации зависит от входного сигнала, который обозначен. Входной сигнал на клеточной поверхности может быть триггером на клеточной мембране или возникать из внеклеточного сигнала. Все эти виды являются функциями пространства и времени, где – точка на мембране, а t – время. Диффузия вдоль клеточной мембраны, которая, как предполагается, представляет собой двумерную изогнутую поверхность в трехмерном пространстве, описывается оператором Лапласа-Бельтрами Δ Γ и коэффициентом диффузии D mem .Поскольку мембрана представляет собой поверхность в трехмерном пространстве с незначительной толщиной, естественной единицей для концентрации видов, связанных с клеточной мембраной P n ( n = 1,…, M ), является молекул на площадь. Молекулярные концентрации сигнальных молекул часто указываются в наномолярных или микромолярных (нМ или мкМ М). Поэтому для удобства мы используем единицы наномолярного или микромолярного временного микрометра ( n M мкм или мкм M мкм ) для мембраносвязанных сигнальных молекул.Обратите внимание, что 1 μ M μ m ≈ 602 мол. / мкм 2 .
Скорости фосфорилирования, а также скорости дефосфорилирования выражаются в единицах молекул на площадь и время. Если входной сигнал однороден в пространстве, то есть все пространственные потоки D mem ∇ Γ P n равны нулю, и система уравнений для мембраносвязанных видов может быть описана эквивалентным система обыкновенных дифференциальных уравнений (Приложение S1).В отличие от связанных с мембраной сигнальных компонентов P 1 ,…, P M , сигнальный компонент P M +1 может свободно диффундировать в цитозоле. Для моделирования интерфейса мембрана-цитозоль нам необходимо включить диффузию в цитозоле и реакции на его границах, которые являются мембранами. Эти процессы моделируются уравнением реакции-диффузии (2) с граничным условием (3) Поскольку P M +1 активируется расположенным выше по потоку компонентом P M , который привязан к мембране, реакция фосфорилирования происходит только на клеточной мембране, но не внутри нее. цитозоль.Таким образом, эта реакция моделируется как граничное условие. Реакции на границе раздела мембрана-цитозоль описываются скоростью фосфорилирования и скоростью инактивации v i , как в единицах молекул на площадь, так и во времени. Вид P M +1 свободно диффундирует в цитозольном объеме со скоростью диффузии D cyt , и поэтому его локальная концентрация описывается в единицах молекул на объем.Скорость дефосфорилирования в цитозоле выражается в молекулах на объем и время. Обратите внимание, что скорость инактивации и v i могут быть вызваны мембраносвязанными фосфатазами или насыщением фосфорилирования на мембране. Оба, v a и v i , составляют кинетику на границе раздела мембрана-цитозоль. Для потока на всех других органеллах, заключенных в мембрану, мы предполагаем условие нулевого потока. (4) Уравнения для компонентов нижестоящего цитозольного каскада читаются (5) Концентрации цитозольных компонентов в положении в цитозольном объеме в момент времени t описываются функциями с n = M + 1,…, N .Для цитозольных компонентов мы предполагаем условия нулевого потока: (6) (7) В классических каскадах MAPK последний компонент каскада, который представляет собой фосфорилированный MAPK, импортируется в ядро. Примеры варьируются от ядерного импорта Hog1 в дрожжах [26, 27] до импорта ERK у млекопитающих [28]. В этом случае граничное условие (7) на ядре для последнего цитозольного компонента P N необходимо изменить на (8) где ϵ представляет собой скорость реакции ядерного импорта на ядерной мембране.Если не указано иное, в данной статье предполагается, что ядро имеет граничное условие нулевого потока.
Мы протестируем и сравним системы с тремя компонентами N = 3, как показано на рис. 1, где пространственное расположение компонентов варьируется. Здесь M = 2 описывает случай двух мембраносвязанных и одного цитозольного элемента (мотив фиг. 1B), а M = 0 – случай только цитозольных компонентов (мотив фиг. 1C). В следующем случае M = 2 упоминается как смешанный мембранно-цитозольный (MMC) и M = 0 как чистый цитозольный (PC) каскад.
Результаты
Смешанный мембранно-цитозольный каскад сильно зависит от размера
Мы начинаем этот раздел с анализа сферической ячейки, а затем обобщаем анализ на ячейки произвольной формы. Далее предполагается сферическая ячейка радиуса R ячейка со сферическим ядром радиусом R nuc , помещенная в центр ячейки.
Входной сигнал обозначен как P 0 ( t ) и предполагается однородным на поверхности ячейки.Концентрации протеинкиназ описываются функциями P i ( r , t ) в зависимости от пространства и времени. Обратите внимание, поскольку клеточная геометрия радиально симметрична и входной сигнал P 0 действует на клеточную мембрану однородно, эти функции зависят только от радиального расстояния от центра клетки, обозначенного r , и времени t . В следующем анализе кинетические скорости линеаризованы, что означает, что мы предполагаем и для фосфорилирования и дефосфорилирования, соответственно.Скорость инактивации v i на границе раздела мембрана-цитозоль также линеаризуется с помощью v i = γP M +1 . Обратите внимание, что кинетика интерфейса может быть переформулирована как, из чего легко увидеть, что активация на мембране насыщается при. Уравнения модели для смешанного мембранно-цитозольного каскада (MMC) с линеаризованной кинетикой читаются следующим образом: (9) (10) (11) и граничные условия для цитозольных видов P 3 : (12) (13)
Существует несколько оценок активности фосфатазы и коэффициентов диффузии для сигнальных компонентов MAPK.Коэффициент диффузии, D cyt , глобулярных цитозольных белков находится в диапазоне 1-10 мкм 2 с -1 , в то время как коэффициент диффузии мембраносвязанных компонентов D mem , намного ниже со значением в диапазоне 10 −3 – 0,1 мкм 2 s −1 [29–31]. Скорости фосфатазы β n колеблются более трех порядков величины 0.1 – 100 с -1 [32, 33]. В случае Fus3, который является MAPK в пути спаривания дрожжей S. cerevisiae , коэффициент диффузии и скорость цитозольного дефосфорилирования были оценены как 4,2 мкм 2 s -1 и 1 с −1 соответственно [14]. См. Таблицу 1 для обзора значений параметров и единиц измерения.
Мы начинаем с анализа стационарного состояния этой системы в интересующих параметрах режимах и предполагаем, что сигнал P 0 является постоянным во времени.Здесь и далее мы обозначаем устойчивое распределение полосой, что означает устойчивое состояние P n . Устойчивое состояние первых двух элементов определяется как и. Для установившегося состояния P 3 решение дается формулой (14) где i 0 и k 0 – модифицированные сферические функции Бесселя первого и второго рода соответственно [37]. Обратите внимание, что i 0 увеличивается с r (расстояние от центра ячейки), а k 0 является убывающей функцией от r .Коэффициенты A и B получены в Приложении S1. Если мы пренебрегаем ядром или в цитозоле нет ядра, то есть R nuc = 0, коэффициент B становится равным нулю. Устойчивое решение для различных размеров ячеек показано на рис. 2.
Рис. 2. Профили внутриклеточной концентрации для двух различных мотивов передачи сигнала.
( A ) Концентрация третьего каскадного элемента P 3 была нанесена на срез через трехмерные ячейки различного размера.Цифры над ячейками указывают их радиус. Внутриклеточные градиенты более крутые для каскада MMC [верхний ряд], чем для каскада ПК [нижний ряд]. Использовались следующие параметры: α 1 = α 2 = α 3 = 1,5 с −1 , β 1 = β 2 = β 3 = 1,0 с -1 , D mem = 0,03 мкм 2 с -1 , D cyt = 3.0 мкм 2 s −1 , γ = 10.0 мкм s −1 , P 0 ≡ 100 n M мкм . ( B ) Размерная зависимость каскада ММС с двумя мембраносвязанными и одним цитозольным типами. ( C ) Размерная зависимость каскада ПК. Ядерная мембрана обозначена пунктирной линией.
https://doi.org/10.1371/journal.pcbi.1006075.g002
Концентрация максимальна на клеточной мембране и уменьшается по направлению к ядру.Оценка длины распада L градиента внутриклеточного градиента (с максимальной концентрацией на мембране) дается [32]. Эту длину затухания можно сравнить с реальным размером ячейки. Их отношение называется модулем Тиле, безразмерной мерой, определяемой как [33]. Для Φ 1 следует ожидать сильных внутриклеточных градиентов и неоднородностей концентраций сигнальных молекул, тогда как для Φ ≪ 1 концентрация почти однородна. Поскольку модуль Тиле связывает коэффициент диффузии и скорость деградации с размером клетки, это важный параметр для исследования формирования градиента [33] и распространения сигнала для нескольких каскадных уровней [38].Однако в трехмерном пространстве L градиент больше не может интерпретироваться как фактический градиент, поскольку его вывод основан на предположении об одномерной геометрии. Кроме того, если предполагается исключительный объем, такой как ядро, одномерный градиент L завышает градиент концентрации. Например, если принять D cyt = 4,0 мкм 2 / s и β = 1.0 с −1 , получаем L градиент = 2,0 мкм . В случае классического одномерного упрощения предполагается распад, пропорциональный ∝ exp (- x / L градиент ), что предполагает уменьшение концентрации на расстоянии x = 2 мкм на коэффициент exp (- x / L градиент ) ≈ 0,37. Однако в сферической ячейке с радиусом R ячейка = 3 мкм с исключенным объемом R nuc = 1 мкм концентрация уменьшается только в 0 раз.77 на расстоянии 2 мкм от клеточной мембраны. Влияние размера клетки на градиенты внутриклеточной концентрации показано на рис. 2.
Зависимость размера клетки в сигнальных системах клетки возникает не только из-за характерного масштаба длины для формирования внутриклеточного градиента, но и из-за изменения средних уровней внутриклеточной концентрации с размером клетки. Мы начинаем с упрощающего предположения, что в цитозоле нет ядра или исключающего объема, что означает R nuc = 0.В этом случае стационарное решение читается как (15) Модифицированные сферические функции Бесселя i 0 и i 1 являются монотонно возрастающими функциями с и. Мы получаем для клеток с малым Φ и, следовательно, реакция фосфорилирования на мембране в этом случае идет при насыщении. Для больших Φ получаем из нижней оценки. Эти оценки справедливы и в случае исключающего объема, которым является ядро, и мы получаем оценку концентрации на клеточной мембране: (16) Зависимость абсолютных уровней концентрации от границы раздела мембрана-цитозоль показана на рис. 2 и 3 для набора различных параметров.При большой скорости инактивации на границе раздела мембрана-цитозоль зависимость размера клеток уменьшается. Следовательно, зависимость размера клеток в основном определяется γ и не зависит от скорости фосфорилирования α .
Рис. 3. Зависимость уровней концентрации от размера и формы клеток.
Средняя концентрация третьего каскадного элемента на клеточной мембране [первая строка], в цитозоле [вторая строка], в ядре [третья строка], а также нормализованная дисперсия [четвертая строка] была нанесена на график относительно клетки. диаметр d x .При изменении d x формы ячеек были пропорционально масштабированы по оси y и z. Использовались следующие параметры: α 1 = α 2 = α 3 = 1,5 с −1 и β 1 = β 2 = β 3 = 1,5 с -1 , D mem = 0,03 мкм 2 с -1 , D cyt = 3.0 мкм 2 s −1 и P 0 ≡ 100 n M мкм . Моделирование каскада MMC [точки] и [крестики] было выполнено для γ = 0 [синий и красный], а также γ = 1,0 мкм s -1 [оранжевый и зеленый]. Средние концентрации в цитозоле абсолютно одинаковы для обоих каскадов [второй столбец]. Для всех форм средняя концентрация точно аппроксимируется Λ 3 (MMC) или (PC), а для γ = 1.0 мкм с -1 аппроксимация слегка завышает среднюю концентрацию (пунктирная линия).
https://doi.org/10.1371/journal.pcbi.1006075.g003
Мы можем дополнительно исследовать эволюцию средних уровней концентрации, которая зависит от концентрации на клеточной мембране и силы внутриклеточного градиента. В случае ячеек произвольной формы с объемом ячейки V ячейка и площадью клеточной мембраны M ячейка , средняя концентрация получается из (17) В [33] аналитические решения для средней концентрации в сферической ячейке и пластине были получены как функции модуля Тиле.Однако, поскольку выводы ограничены геометрией клеток, где доступно явное аналитическое решение уравнения реакции диффузии, мы вводим альтернативный подход для оценки средних уровней концентрации в зависимости от цитозольного объема и площади клеточной мембраны. Поскольку сигнал распространяется от клеточной мембраны в цитозоль, клеточную мембрану можно рассматривать как источник, в то время как цитозольный объем, в котором фосфорилированные сигнальные молекулы дефосфорилируются, можно рассматривать как сток.Эта идея может быть получена математически путем интегрирования уравнения (2) и применения теоремы Грина, что приводит к (18) Здесь продукция в левой части уравнения зависит от площади клеточной мембраны, которая уравновешивается деградацией в цитозоле в правой части уравнения. На основе уравнения сохранения массы (см. Приложение S1) в реакционно-диффузионных системах мы вводим следующую меру: (19) Эта мера имеет свойство γ = 0 или β = 0, что справедливо для произвольной формы ячеек.Кроме того, для сферической ячейки оценка верна для β > 0 и γ > 0 (см. Приложение S1 и рис. 3). Поэтому мы используем Λ M +1 в качестве заместителя для средней концентрации для произвольной формы ячеек, которую можно легко вычислить.
Сравнение оценки Λ 3 со средней концентрацией показано на рис. 3 для различных форм ячеек, которые представляют собой сферическую ячейку, ячейку в форме стержня, ячейку с одним выступом и ячейку с двумя выступами.Эти формы клеток встречаются, например, у S. cerevisiae , S. pombe и гаплоидных S. cerevisiae , стимулированных феромоном спаривания [39, 40]. Для этих форм с различным размером ячеек моделировался каскад MMC. Мера Λ 3 является точным предиктором средней концентрации в случае γ = 0 для всех форм клеток и немного завышает среднюю концентрацию для γ = 1 мкм s −1 .
Кроме того, мы исследовали различия концентраций между клеточной мембраной и ядром и сравнили их со средней концентрацией в цитозоле. Для сферической клетки средние уровни концентрации в цитозоле, а также на мембране были самыми низкими, что и следовало ожидать, поскольку отношение поверхности к объему является самым низким среди всех форм. Различия в концентрациях между мембраной и ядром были самыми высокими для сферической клетки и клетки с двумя выступами, а средняя концентрация в ядре снизилась почти до нуля для крупных клеток.Для ячейки в форме стержня разница концентраций была наименьшей, так как расстояние вдоль короткой оси мало и концентрация не падает так резко, как для других форм ячейки.
Кроме того, мы установили соответствие эволюции средних уровней концентрации во времени. В случае γ = 0 и произвольной формы ячеек средние уровни концентрации подчиняются системе обыкновенных дифференциальных уравнений (20) (21) (22) где и – средние уровни концентрации в молекулах на площадь клеточной мембраны.Эта система обыкновенных уравнений может быть получена путем интегрирования уравнений (9) – (13) по их соответствующим пространственным областям. См. Приложение S1 для получения подробной информации. Устойчивое состояние для средней концентрации определяется выражением (23) Следовательно, средний уровень концентрации зависит от отношения площади мембраны к цитозольному объему, которое определяется выражением. Таким образом, эффективная скорость глобального фосфорилирования для средней концентрации активных сигнальных молекул в цитозоле определяется величиной. Эти соотношения дают нам соответствие между широко распространенными обыкновенными дифференциальными уравнениями и уравнениями в частных производных для объемной поверхности, используемыми в этой статье.Таким образом, мы имеем сильную зависимость от размера ячеек с уменьшением концентрации для более крупных ячеек.
Эффективный цитозольный транспорт через цитозольные каскады
Далее мы рассматриваем чистый цитозольный (PC) каскад с тремя элементами, в котором все элементы свободно диффундируют через цитозоль. Система реакции-диффузии задается формулой (24) (25) (26) с граничными условиями на мембране (27) (28) и в ядре (29) (30) Обратите внимание, что интерфейс мембрана-цитозоль происходит на первом каскадном уровне, что означает, что только P 1 активируется на мембране со скоростью α 1 P 0 – γP 1 .В частном случае β 1 = β 2 = β 3 = β аналитические аппроксимации цитозольных каскадов в одномерной системе были получены в [41, 42]. В то время как одномерная клеточная геометрия может использоваться для качественного изучения формирования градиента, пространственные эффекты, такие как отношение поверхности клетки к объему, не учитываются. Таким образом, мы получили точные аналитические решения линейной системы в трех измерениях.Устойчивые решения для расширяются следующим образом (31) Алгебраические выражения коэффициентов A n , k и B n , k и их вывод приведены в Приложении S1. По сравнению с каскадом MMC, который обсуждался в предыдущем разделе, третий элемент каскада P 3 более равномерно распределен в ячейке, а градиенты концентрации гораздо более мелкие (см. Рис. 2).
Чтобы количественно определить разницу концентраций в ячейке произвольной формы, мы измеряем дисперсию концентрации в ячейке. Поэтому введем дисперсию как (32) Эта мера близко соответствует дисперсии при анализе изображений [43, 44]. В отличие от анализа изображений, где квадрат отклонения интенсивности флуоресценции от средней интенсивности флуоресценции маркера интегрируется по пикселям, интеграция здесь является непрерывной. Что касается аналога в анализе изображений, нормализованная дисперсия рассчитывается как мера отклонения от среднего [44, 45].Хотя эта мера часто используется в алгоритмах автофокуса при анализе изображений, мы предлагаем нормализованную дисперсию в качестве меры степени локализации сигнальных молекул внутри клетки. Оценка распространения нормализованной дисперсии в цитозольном каскаде дается выражением (33) Здесь C s – постоянная величина, зависящая от формы ячейки, а d – диаметр ячейки. Обратите внимание, что C = C s d – постоянная Пуанкаре из хорошо известного неравенства Пуанкаре [46].Для выпуклой формы ячеек оценка верна для. В случае выпуклой формы клетки небольшой клетки дрожжей (без выступа), следовательно, мы имеем оценку C n ≈ 0,3 ≤ 1 для D cyt = 3 мкм 2 / s , α n = β n = 1 s −1 и диаметр ячейки d = 6 мкм . Для этого набора параметров нормализованная дисперсия уменьшается по крайней мере на 70% на уровне второго цитозольного каскада и на 90% на уровне третьего цитозольного каскада (по сравнению с первым элементом каскада).В целом, для C n <1, нормализованная дисперсия внутриклеточных концентраций уменьшается с увеличением уровня каскада, и различия концентраций в клетке уравновешиваются (см. Фиг.3).
Как и в предыдущем разделе, мы получили оценку средней концентрации. В этом случае мы использовали оценку Λ 1 к, поскольку P 1 является каскадным элементом, который активируется на границе мембрана-цитозоль для каскада ПК.Средняя концентрация связана с величиной, поэтому мы использовали приближение для. Как и в случае с MMC, это приближение является точным для γ = 0 и слегка завышает среднюю концентрацию для γ = 1 мкм s −1 (см. Рис. 3).
Точные выражения для стационарных состояний средней концентрации сигнальных компонентов в случае γ = 0 и для произвольной формы клеток даются формулами (34) Следовательно, средняя концентрация третьего элемента каскада принимает одинаковые значения в каскаде ММС и ПК.Основное различие обоих пространственных мотивов заключается в том, что различия концентраций, полученные на клеточной мембране и ядре, больше в каскаде MMC, чем в каскаде PC. Как и в предыдущем разделе, мы можем сформулировать систему обыкновенных дифференциальных уравнений для временной эволюции средних концентраций (35) (36) (37) Зависимость абсолютных уровней концентрации от границы раздела мембрана-цитозоль показана на рисунке 2 и рисунке в приложении S1 для набора различных параметров.
Время пространственной сигнализации
Анализ изображений с временным разрешением показал, что сигнальные пути MAPK отвечают измеряемым сигналом в ядре во временных масштабах от секунд до нескольких минут. Ответ пути Hog1 (фосфорилированный MAPK) у почкующихся дрожжей составляет примерно 80% от его максимальной активности в течение минуты [26]. Другой пример – цикл активации / деактивации Src, в котором колебания и импульсы происходят в режиме секунд [47]. Синхронизация передачи сигнала в линейных сигнальных каскадах для хорошо перемешанных гомогенных систем была проанализирована в [9].Они пришли к выводу, что для слабо активируемых сигнальных каскадов фосфатазы оказывают более выраженное влияние, чем киназы, на скорость и продолжительность передачи сигналов, тогда как амплитуда сигнала контролируется в основном киназами. Тщательный анализ линейных моделей, предполагающих однородное распределение сигнальных молекул для различных видов внешних стимулов, был недавно разработан в [12]. Мы расширили и сравнили эти результаты с пространственной трансдукцией сигнала без упрощения гомогенных концентраций.Сколько времени нужно для установления градиента внутриклеточной концентрации? Как диффузия изменяет время передачи сигнала от клеточной мембраны к ядру? Какие различия концентраций ожидаются, пока не установится устойчивое состояние? Анализ шкалы времени для пространственных моделей сложнее, чем для моделей, основанных на предположениях, смешанных по волеизъявлению, из-за высоких вычислительных затрат. Поэтому мы использовали недавно введенную меру времен накопления [25, 48]. Приближение P n ( r , t ) к его устойчивому состоянию на радиальном расстоянии r от центра ячейки и времени t можно охарактеризовать с помощью функции локальной релаксации. (38) Разницу ρ n ( r , t 1 ) – ρ n ( r , t 2 ) можно интерпретировать как долю установившийся уровень, накопленный за интервал времени [ t 1 , t 2 ].В бесконечно малом временном интервале [ t , t + dt ] доля накопленных активированных сигнальных молекул в устойчивом состоянии выражается выражением. Время локального накопления определяется как [25] Время накопления может быть получено из стационарного решения, даже если не известна замкнутая форма зависящего от времени решения [25].
Временные характеристики средних концентраций, указанные в системе обыкновенных дифференциальных уравнений для каскада ММС (20) – (22) и каскада ПК (35) – (37), одинаковы и могут быть аналитически выражены как (39) Это выражение также совпадает с временами передачи сигналов, рассчитанными Heinrich et al.[9]. Однако для пространственной модели время локального накопления на мембране и ядре различается. Накопление обычно происходит быстрее на мембране и медленнее в ядре, где степень различия увеличивается с размером клетки (см. Рис. 4). Более того, два пространственных мотива обнаруживают существенные различия. Для каскада MMC время накопления для второго элемента P 2 находится точно на мембране, в то время как для цитозольных видов оно короче (сравните Рис. 4).
Рис. 4. Синхронизация пространственной сигнализации.
Было смоделировано время передачи сигналов для смешанного мембранно-цитозольного (MMC) каскада [слева] и чистого цитозольного (PC) каскада [справа] на мембране и в ядре. ( A ) График зависимости от времени концентраций P 1 , P 2 и P 3 после стимуляции зависимым от времени сигналом и был нанесен на график. Уровни каскада обозначены цифрами. Обратите внимание, что в случае MMC концентрации для P 1 и P 2 приведены в n M мкм , а концентрация P 3 дана в n. М.Для каскада ПК все концентрации P 1 , P 2 и P 3 приведены в n M. Использованные параметры: R ячейка = 6 мкм , R nuc = 2 мкм , λ = 1 с −1 , α 1 , α 2 , α 3 = 1.0 s – 1 , β 1 , β 2 , β 3 = 0.5 с -1 , D mem = 0,03 мкм 2 с -1 и D cyt = 3,0 мкм 2 03 с 1 . Эта установка была смоделирована для γ = 0 и γ = 1 мкм / s . ( B ) Время накопления для смешанного мембранно-цитозольного каскада. В этом сценарии применялся постоянный сигнал и варьировался размер ячейки.Отношение сотового радиуса к ядерному было сохранено на уровне R cell / R nuc = 3. В остальном использовали те же параметры, что и в ( A ).
https://doi.org/10.1371/journal.pcbi.1006075.g004
Время накопления P 3 в ядре, как и ожидалось, намного больше. Для маленьких клеток внутриклеточная концентрация является пространственно однородной и приближение сохраняется, в то время как время распространения сигнала к ядру увеличивается с размером клетки.Аналитическое решение времен накопления для P 3 для каскада MMC и частного случая R nuc = 0 может быть получено [49], которое приведено в Приложении S1. Однако для более крупных клеток время распространения сигнала к ядру увеличивается с размером клетки. Для каскада ПК увеличение времени накопления в ядре с увеличением размера клетки менее выражено, чем для смешанного цитозольного каскада мембран.
В то время как для расчета времени накопления применялся постоянный стимул, мы также тестировали затухающий сигнал с помощью и численно решили систему, зависящую от времени.Сравнение MMC и PC показано на рис. 4. Интересно, что уровень концентрации на мембране для каскада ПК снижается от первого каскада P 1 до второго каскада P 2 и более снова увеличивается от второго каскадного вида P 2 к третьему каскадному виду P 3 , в то время как наблюдается увеличение от предыдущего каскадного вида к следующему каскадному виду в ядре.Это явление вызвано разницей концентраций от клеточной мембраны к ядру, которая для P 1 больше, чем для P 2 в каскаде ПК. Обратите внимание, что параметры были выбраны равными, что означает двукратное увеличение средних уровней концентрации от одного элемента сигнального каскада к другому. Следовательно, пространственная система может вести себя совершенно иначе, чем однородная система. Время накопления на мембране было намного быстрее для γ = 1 мкм / с , чем для γ = 0, и лишь незначительно изменялось с размером ячейки.Однако для более крупных клеток время накопления сигнала в ядре практически не зависело от γ . Следовательно, разница во времени накопления на мембране и ядре увеличилась с γ (также сравните рисунок в Приложении S1). В случае каскада MMC время накопления в ядре для клетки с R клетки = 12 мкм почти удвоилось по сравнению с маленькой клеткой с R ячейкой = 2 мкм , а для В каскаде ПК увеличение времени накопления с размером клеток было менее выраженным.
Для вычисления высших моментов шкалы времени и частного случая клетки без ядра мы ссылаемся на [49]. Анализ временного масштабирования линейного каскада в одном пространственном измерении с четырьмя элементами, включая высшие моменты, был проведен в [50].
Количественная оценка чувствительности пути к пространственно неоднородным сигналам
Далее мы анализируем преобразование разнородных внешних сигналов. Например, в культурах популяций смешанных гаплоидных дрожжевых клеток [40], а также в микрофлюидных устройствах [51] внешний сигнал феромона, который запускает каскад MAPK, не распределяется однородно, а образует градиенты во внеклеточной среде.Активированный сигнальный каскад пространственно локализован и запускает последующий направленный рост S. cerevisiae [14], а также S. pombe [15]. Более того, свойства белок-белковых взаимодействий и морфологические изменения могут быть тесно связаны [52].
Таким образом, мы исследуем передачу сигнала в ответ на внешний гетерогенный сигнал для клеток той же формы, что и на рис. 3, которые представляли собой сферическую ячейку, ячейку в форме стержня, ячейку с одним выступом и ячейку с двумя выступами.Эти формы клеток встречаются, например, у S. cerevisiae , S. pombe и во время их реакции на стимуляцию феромоном спаривания [53].
Мы протестировали линейный сигнальный каскад с градуированным стимулом вида (40) где и – константы, описывающие базовую мощность сигнала и крутизну сигнала соответственно. Здесь мы выбрали начало координат в центре ячейки и, следовательно,. Таким образом, мы получаем градиент входного сигнала, который линейно увеличивается в направлении x 1 для и линейно уменьшается для.Концентрация при дается выражением.
Мы проверили влияние асимметрии формы клеток в ответ на градиентный стимул (40) и исследовали пространственное распределение последнего сигнального компонента каскада MMC и PC, который равен P 3 . На рис. 5 (A) и 5 (C) профиль концентрации на клеточной мембране, а также вдоль среза клетки в ответ на гомогенный сигнал показан в качестве контроля. Поскольку сферическая ячейка радиально симметрична, градиент на мембране не индуцировался.Для стержневой клетки мы наблюдали неглубокий градиент на поверхности клетки с более высокой концентрацией на полюсах, профиль внутриклеточной концентрации показал две области с низкой концентрацией, которые были разделены ядром. Этот эффект был более выражен для каскада ММС. Для каскада ПК концентрация была почти однородной. Для клеток асимметричной формы с одним и двумя выступами в ответ на однородный входной сигнал был установлен градиент от дистального конца (передний) к сферической части (сзади).Выступ, следовательно, можно сравнить с карманом, в котором устанавливаются более высокие концентрации цитозольных сигнальных молекул. Математически этот эффект можно объяснить геометрической зависимостью собственных функций оператора Лапласа [54], которая может быть использована для характеристики решения уравнений реакции-диффузии для определенной геометрии ячейки. Следовательно, эти асимметричные формы клеток уже могут индуцировать градиент сигнальных молекул спереди назад.
Рис 5.Отклик двух каскадных систем, MMC и PC, для различных форм клеток на изменение градиента сигнала.
( A ) Пространственный профиль концентрации на клеточной мембране, а также вдоль среза клетки в ответ на однородный входной сигнал P 0 ≡ 100 n M мкм . Сферическая ячейка имеет размер R ячейка = 2,5 мкм с ядром радиусом R ядро = 1 мкм .Все формы клеток имеют одинаковый объем клеток и содержат сферическое ядро одинакового размера. ( B ) Моделирование для переменного размера ячейки, измеренного как диаметр d x в x-направлении и трех различных наклонах сигнала (зеленый), 0 (оранжевый), 0,03 мкм −1 (красный) были выполнены. Градиент градиента был нанесен. Вот и находятся крайние точки x – направление на клеточную мембрану или ядро. В ( C ) и ( D ) каскады ПК моделировались для той же установки, что и в ( A ), ( B ).Использовались следующие параметры: α 1 = α 2 = α 3 = 1 с −1 , β 1 = β 2 = β 3 = 1 с −1 , γ = 0,5 мкм с −1 , D mem = 0,03 мкм 2 −1 и D cyt = 3.0 мкм 2 с −1 .
https://doi.org/10.1371/journal.pcbi.1006075.g005
На рис. 5 (B) и 5 (D) отклики на сигнал с, увеличивающимся в направлении x 1 . , и сигнал с, который уменьшается в направлении x 1 , были смоделированы и противопоставлены ответу на пространственно однородный сигнал с. Для измерения отклика мы естественным образом определяем градиент n -го элемента каскада как разность концентраций в двух точках на евклидовом расстоянии этих двух точек.В случае концентраций киназы градиент рассчитывали из. Здесь и находятся крайние точки в x 1 -направлении на клеточной мембране или ядре. Оба мотива, каскад MMC и PC, по-разному ведут себя при передаче градиентов сигнала. Градиент уровня третьего каскада P 3 вдоль клеточной мембраны и ядра уменьшался для каскада MMC с размером клеток для всех форм. Для ПК градиент увеличивался с размером ячейки до максимального значения, а затем уменьшался с увеличением размера ячейки, что предполагает оптимальный размер ячейки для обнаружения и передачи градиента.Этот эффект был ожидаемым, поскольку для маленьких клеток концентрация в цитозоле была почти однородной, а различия в концентрациях уравновешивались диффузией. Однако с увеличением размера клетки средний уровень концентрации в клетке и ядре снижался. Как следствие, также уменьшился абсолютный градиент.
Ячейка в форме стержня показала более сильный отклик, чем ячейка сферической формы, поскольку концентрации были выше на полюсах и ячейка была выровнена по градиенту.Кроме того, компартментализация, индуцированная ядром в клетке в форме тонкого стержня, оказывала выраженное влияние на градиент P 3 , поскольку диффузия в цитозоле спереди назад была затруднена. Для ячеек с одним и двумя выступами градиент P 3 был сильно смещен с увеличением направления выступов. Обратите внимание, что оба мотива ведут себя по-разному при передаче градиента ядру. В то время как для каскада MMC зависимость формы была более выраженной, а градиент внутри клетки был почти отделен от градиента на мембране для асимметричных форм клеток, каскад ПК передавал градиент более надежно внутрь клетки и в ядро.
Итак, мы наблюдали сильное влияние размера клеток на локализацию и установление градиентов с помощью элементов сигнального каскада. Для ячейки с выступом концентрация P 3 в выступе была выше, чем в противоположном дистальном конце, который является сферической частью ячейки. Этот эффект возник из-за более высокого отношения локальной поверхности к объему в области выступа. Следовательно, большая часть цитозольных сигнальных молекул, которые свободно диффундируют в цитозоле, фосфорилируется в части выступа, приводя к градиенту от кончика выступа к противоположному дистальному концу клетки.Влияние клеточной асимметрии также исследовалось в [23] для градиентов малой Rho-GTPase Cdc42 во время клеточной поляризации. Однако эта система реагирует противоположным образом, поскольку поток молекул во время установления сайта полярности направлен из цитозоля на мембрану и, следовательно, устанавливается градиент от дистального конца к выступу.
Эти эффекты возникают из-за разной архитектуры обеих систем. В сигнальных каскадах ПК и ММС происходит передача сигнала от мембраны к ядру и, следовательно, диффузионный поток активированных сигнальных молекул из мембраны в цитозоль, тогда как в системе поляризации поток сигнальных молекул во время установления сайт полярности направлен из цитозоля на мембрану, что является противоположным направлением.Следовательно, обе системы по-разному реагируют на клеточную асимметрию в отношении образования градиента. Это взаимодействие обеих систем особенно интересно, поскольку у многих организмов поляризационная система взаимодействует с каскадом MAPK [55, 56] и, следовательно, может точно контролировать форму и размер клеток.
Для сферической формы ячеек мы, кроме того, исследовали более сложные градиенты внешнего сигнала, то есть неоднородности с множеством максимумов и минимумов (см. Приложение S1). Как и в [18, 57], неоднородный сигнал на сфере можно разложить с помощью сферических гармоник (41) (42) В этом разложении амплитуды более высокого порядка, где порядок обозначен как -1, обычно более сильно затухают, чем градиенты или пространственные неоднородности более низкого порядка.Таким образом, результаты, показанные здесь, могут быть расширены до сложных пространственных сигналов на поверхности клетки. Мы предоставляем полные аналитические решения для MMC и PC для сферы без ядра (см. Приложение S1).
Системы с обратной связью
В этом разделе мы анализируем влияние размера клетки на передачу сигнала для осциллирующего каскада, состоящего из двух мембраносвязанных и одного цитозольного элемента (MMC), и каскада из трех цитозольных элементов (PC), то есть для M = 2 и M = 0 соответственно.Далее исследуется случай отрицательной обратной связи и постоянного однородного сигнала.
Отрицательные обратные связи являются частым элементом регуляции сигнальных каскадов и могут быть индуцированы дефосфорилированием вышележащих компонентов с помощью MAPK или фосфатаз [39, 58–61]. Примеры представлены фосфатазами Tyr, которые могут вызывать отрицательную обратную связь [47], и фосфатазами двойной специфичности (DUSP) [59]. Некоторые отрицательные обратные связи, например, индуцированные в цикле Src-Tyr, приводят к колебаниям на временной шкале секунд [47], в то время как другие действуют на гораздо более длительных временных масштабах.Например, во время дрожжевой феромонной реакции MAPK Fus3 подвергается устойчивым колебаниям в течение 2-3 часов, которые контролируют периодическое образование спаривающихся выступов. В этом процессе Sst2 действует как негативный регулятор передачи сигналов G-Protein на мембране, тогда как дезактивация в цитозоле опосредуется MAPK фосфатазой Msg5 [39]. Классическим и наиболее простым примером осциллятора с отрицательной обратной связью и нелинейными членами реакции является колебательная система Гудвина [62, 63].
Мы адаптируем упомянутую модифицированную систему и формулируем задачу, используя уравнения в частных производных, добавляя диффузионный член и формулируя граничные условия в соответствии с моделями, упомянутыми ранее. Скорости фосфорилирования и дефосфорилирования для обеих моделей читаются как (43) (44) (45) согласно уравнениям (1) – (5) соответственно. Скорость активации содержит отрицательную обратную связь, поскольку высокая концентрация P 3 приводит к более низкой активации P 1 .Предположим постоянный внешний сигнал.
Для первой модели (MMC) деактивация со скоростью происходит в цитозоле, тогда как активация происходит на мембране и поэтому моделируется как граничное условие с v i = 0 согласно уравнениям (2 ) и (3), поскольку P 3 является исключительно цитозольным видом. Мы предполагаем условия нулевого потока для P 3 на ядре, что означает, что мы устанавливаем скорость реакции ядерного импорта ϵ = 0 (сравните уравнение (8)).
Для второй модели (PC) все виды являются исключительно цитозольными, поэтому скорость активации для P 1 является граничным условием, описывающим активацию P 1 на мембране. Мы предполагаем условие нулевого потока для P 3 на ядре ( ϵ = 0) и для P 1 и P 2 как на ядре, так и на мембране, что означает всю границу.
Обе модели имеют нелинейную кинетику, а также отрицательную обратную связь, приводящую к колебаниям.Кроме того, в обеих моделях скорость активации для P 1 зависит от параметра p > 0. Это показано, например, в [64], что для p > 8 система ODE, состоящая из трех компонентов, дестабилизируется, а для более длинных каскадов, т.е. для большего N , система становится нестабильной для еще более низких значений p > 1.
Поскольку аналитическое решение для обеих моделей неизвестно, для решения систем необходимо использовать численные методы.По причинам простоты и из-за больших вычислительных затрат мы решили системы в двух измерениях, используя диск для моделирования ячейки. Мы использовали схему с фиксированной точкой для решения нелинейных уравнений.
Мы выбрали параметры β 1 = β 2 = β 3 = 0,125 с −1 , D cyt = 1 мкм 2 0 с −1 , D mem = 0.01 мкм 2 s −1 , R nuc = 1 мкм и R ячейка = 2 мкм . Начальные условия: P 1 = P 2 = 10 n M мкм и P 3 = 10 n M для каскада MMC и P 1 = P 2 = P 3 = 10 n M для каскада ПК.Для K m = 100 n M и силы обратной связи p = 10, обе модели колебались, как и ожидалось, рис. 6A.
Рис. 6. Колебания в зависимости от размера в системе с отрицательной обратной связью.
( A ) Средняя концентрация P 1 , P 2 и соответственно P 3 с течением времени. После начального пика обе системы колеблются. Обратите внимание, что в случае MMC, P 1 , P 2 уровни концентрации даны в n M мкм , тогда как P 3 концентрация дана в n M.Для каскада ПК все концентрации P 1 , P 2 и P 3 приведены в n M. ( B ) Частотный анализ средней концентрации обеих моделей для последний вид, P 3 . ( C ) Частота и амплитуда средней концентрации P 3 для двух моделей в зависимости от размера ячейки.
https://doi.org/10.1371 / journal.pcbi.1006075.g006
Следовательно, в случае относительно небольшого размера ячейки R ячейка = 2 мкм , обе пространственные модели ведут себя аналогично исходной модели, которая была сформулирована как система обыкновенных дифференциальных уравнений. Анализ частот колебаний и средней концентрации можно увидеть на рис. 6В. Основываясь на предыдущих экспериментах и графиках, частотный анализ был проведен после t = 200 s , когда частоту и соответствующие амплитуды средних концентраций для обеих моделей можно считать постоянными.Обе модели показывают очень похожее поведение, тогда как частота и средняя концентрация выше для чистой цитозольной модели, что можно объяснить тем фактом, что реакции происходят не только на мембране, но и повсюду в цитозоле.
На следующем этапе мы изменили размер ячейки 1,5 мкм ≤ R ячейка ≤ 4,0 мкм и снова провели анализ частот и соответствующих амплитуд для обеих моделей. Результаты анализа третьего компонента обеих моделей представлены на рис. 6С.Как указывалось ранее, частота для обеих моделей очень похожа, но амплитуда сигнала выше для цитозольной модели.
Колебания в первой, смешанной каскадной модели возникают только для размера ячейки до R ячейка ≤ 2,5 мкм , а во второй, чистой цитозольной модели для размера ячейки до R ячейка ≤ 3,0 мкм . Начальные колебания быстро затухают, и обе модели сходятся к установившемуся состоянию, если размер ячейки выбран больше.
Discussion
Стимулируемые прогрессом в области визуализации клеток и растущей потребностью в понимании внутриклеточной динамики, мы исследовали и обсудили общий подход к моделированию передачи клеточного сигнала во времени и пространстве. Сигнальные каскады ковалентных модификаций белков, такие как каскады митоген-активируемых протеинкиназ (MAPK) и небольшие каскады GTPase, встречаются во множестве вариаций [1, 13, 65]. Первый сигнальный компонент может быть активирован на клеточной мембране с помощью связанного с мембраной фермента, такого как киназа или фактор обмена гуаниновых нуклеотидов в передаче сигналов GTPase, в то время как дезактивация может происходить на мембране или в цитозоле, например, опосредованной фосфатазой. или белок, активирующий ГТФазу [66].Следовательно, активация и деактивация могут быть пространственно разделены, что создает ряд различных пространственных расположений и комбинаций при передаче сигнала.
Мы исследовали сигнальные каскады с различным пространственным расположением сигнальных компонентов. Мы показали, что моделирование интерфейса мембрана-цитозоль имеет решающее значение, а также соотношение площади мембраны и цитозольного объема, которые являются пространственными свойствами. Результаты указывают на сильную зависимость передачи сигнала внутри клеток от размера и формы клеток, которые, вероятно, вносят вклад в изменение отдельных клеток в ответ на внеклеточные стимулы.Мы предлагаем, чтобы клетки измеряли отношение клеточной мембраны к объему клетки, чтобы координировать рост и дифференцировку. Для асимметричных форм клеток также важны локальные изменения в соотношении объема клетки к клеточной мембране для внутриклеточной передачи сигналов. Широко используемые зависящие от времени модели обыкновенных дифференциальных уравнений могут быть естественным образом распространены на пространство с помощью дифференциальных уравнений объемной поверхности. Применяя это расширение к классу моделей линейной передачи сигнала, мы сравнили предположение о хорошо перемешанной клетке с двумя различными мотивами передачи пространственного сигнала.Мы вывели и обсудили критерии, которые можно использовать для проверки хорошо смешанного предположения, и показали, что кинетика, которая связывает мембраносвязанные виды с цитозольными видами, естественным образом вызывает зависимость от размера. Таким образом, результаты имеют важное значение для кинетических моделей передачи сигналов.
Наши результаты имеют важное биологическое значение. Поскольку сигналы, передаваемые линейными сигнальными каскадами от клеточной мембраны к ядру, экспоненциально уменьшаются в масштабе нескольких микрон, наши теоретические результаты предполагают сильную зависимость размера клетки в ответ на внеклеточные стимулы.Кроме того, отношение общего объема клетки к площади клеточной мембраны важно для средних уровней концентрации. Проекции спаривания, возникающие у дрожжей, действуют как карманы для сигнальных молекул, которые могут поддерживать биохимические обратные связи. Адаптации в виде ламеллиподий в кератоцитах или инвагинаций, таких как Т-канальцы в миоцитах, могут локально увеличивать накопление сигнальных молекул. Эти клеточные структуры способны напрямую обеспечивать обратную связь при передаче сигналов.
Мы предлагаем нормированную дисперсию в качестве меры для количественной оценки различий в концентрациях и локализации сигнальных молекул, которые могут быть получены из данных микроскопии с пространственным разрешением в дополнение к средним уровням интенсивности флуоресцентного маркера.Например, было бы полезно измерить среднюю концентрацию и нормированную дисперсию вместе с размером и морфологией клеток. В интересных исследованиях ответа в популяциях клеток часто отсутствует поведение ответа, связанное с размером и морфологией клеток. Примеры варьируются от поведения переключателя в популяциях ооцитов [67] до феромонного ответа в дрожжевых клетках [68, 69]. Следовательно, данные об отдельных клетках, в которых размер клетки назначается этим измерениям, необходимы для точного количественного исследования пути, чтобы отделить биохимические свойства белок-белковых взаимодействий и морфологические свойства, такие как размер и форма целых клеток.Нацеливание на сигнальные белки с помощью модификаций липидирования, таких как пальмитоилирование, пренилирование или миристоилирование [2, 3, 5], может изменить секвестрацию сигнального каскада с чистого цитозольного (PC) каскада на каскад со смешанными мембранами (MMC). В случае ММС со смешанной мембраной зависимость от геометрии и размера более выражена, поскольку первые сигнальные элементы привязаны к мембране. Напротив, для исследуемого каскада ПК локализация и сильные внутриклеточные градиенты уменьшаются, но в зависимости от кинетических параметров геометрическая информация также может лучше передаваться по всей клетке.
В нелинейных сигнальных системах различия, которые мы наблюдали в моделях линейных сигнальных каскадов, вероятно, будут усиливаться. Нелинейная кинетика может усиливать образование градиента, что приводит к еще более сильным различиям внутриклеточных концентраций [70]. Это также справедливо для уровней абсолютной концентрации, которые могут переключаться в зависимости от кинетики [67, 71]. Более того, кинетика более высокого порядка может усиливать разницу во времени накопления в разных клеточных местоположениях [72], что может приводить к пространственным колебаниям и фосфопротеиновым волнам.
Анализ модели сигнального каскада может быть расширен на более сложные пространственные неоднородности, например, с помощью ряда Лапласа, как предложено в [18, 57]. С помощью этого подхода могут быть представлены локализованные сигналы, возникающие из мембранных структур, таких как липидные рафты, септины или совместная локализация из-за белок-белковых взаимодействий. Так как они часто являются предшественниками формы клеток и структур органелл, взаимодействие с формой и морфологией клеток должно быть рассмотрено в будущих исследованиях.Зависимость внутренней геометрии сигнальных систем недавно была показана для эллипсоидальных форм клеток в системе MinE-MinD [24, 73, 74], но также и в дрожжевой системе [23, 75–77]. Ожидается, что недавние разработки математических методов, таких как метод конечных элементов для уравнений объемной поверхности [19, 20], а также методы анализа устойчивости этих систем [23, 78–82], дадут дальнейшее понимание поведения передачи клеточного сигнала.

 /попер., Н/5см: 177/129
/попер., Н/5см: 177/129 Они не входят в
гидрофобное ядро мембраны.
Они не входят в
гидрофобное ядро мембраны.