Чем измеряют – Измерение величин, меры, единицы измерения

Измерение величин, меры, единицы измерения

Величина – это то, что можно измерить. Такие понятия, как длина, площадь, объём, масса, время, скорость и т. д. называют величинами. Величина является результатом измерения, она определяется числом, выраженным в определённых единицах. Единицы, в которых измеряется величина, называют единицами измерения.

Для обозначения величины пишут число, а рядом название единицы, в которой она измерялась. Например, 5 см, 10 кг, 12 км, 5 мин. Каждая величина имеет бесчисленное множество значений, например длина может быть равна: 1 см, 2 см, 3 см и т. д.

Одна и та же величина может быть выражена в разных единицах, например килограмм, грамм и тонна – это единицы измерения веса. Одна и та же величина в разных единицах выражается разными числами. Например, 5 см = 50 мм (длина), 1 ч = 60 мин (время), 2 кг = 2000 г (вес).

Измерить какую-нибудь величину – значит узнать, сколько раз в ней содержится другая величина того же рода, принятая за единицу измерения.

Например, мы хотим узнать точную длину какой-нибудь комнаты. Значит нам нужно измерить эту длину при помощи другой длины, которая нам хорошо известна, например при помощи метра. Для этого откладываем метр по длине комнаты столько раз, сколько можно. Если он уложится по длине комнаты ровно 7 раз, то длина её равна 7 метрам.

В результате измерения величины получается или именованное число, например 12 метров, или несколько именованных чисел, например 5 метров 7 сантиметров, совокупность которых называется составным именованным числом.

Меры

В каждом государстве правительство установило определённые единицы измерения для различных величин. Точно рассчитанная единица измерения, принятая в качестве образца, называется эталоном или образцовой единицей. Сделаны образцовые единицы метра, килограмма, сантиметра и т. п., по которым изготавливают единицы для обиходного употребления. Единицы, вошедшие в употребление и утверждённые государством, называются

мерами.

Меры называются однородными, если они служат для измерения величин одного рода. Так, грамм и килограмм – меры однородные, так как они служат для измерения веса.

Единицы измерения

Ниже представлены единицы измерения различных величин, которые часто встречаются в задачах по математике:

Меры веса/массы

• 1 тонна = 10 центнеров
• 1 центнер = 100 килограмм
• 1 килограмм = 1000 грамм
• 1 грамм = 1000 миллиграмм

Меры длины

• 1 километр = 1000 метров
• 1 метр = 10 дециметров
• 1 дециметр = 10 сантиметров
• 1 сантиметр = 10 миллиметров

Меры площади (квадратные меры)

• 1 кв. километр = 100 гектарам
• 1 гектар = 10000 кв. метрам
• 1 кв. метр = 10000 кв. сантиметров
• 1 кв. сантиметр = 100 кв. миллиметрам

Меры объёма (кубические меры)

• 1 куб. метр = 1000 куб. дециметров
• 1 куб. дециметр = 1000 куб. сантиметров
• 1 куб. сантиметр = 1000 куб. миллиметров

Рассмотрим ещё такую величину как литр. Для измерения вместимости сосудов употребляется литр. Литр является объёмом, который равен одному кубическому дециметру (1 литр = 1 куб. дециметру).

Меры времени

• 1 век (столетие) = 100 годам
• 1 год = 12 месяцам
• 1 месяц = 30 суткам
• 1 неделя = 7 суткам
• 1 сутки = 24 часам
• 1 час = 60 минутам
• 1 минута = 60 секундам
• 1 секунда = 1000 миллисекундам

Кроме того, используют такие единицы измерения времени, как квартал и декада.

• квартал – 3 месяца
• декада – 10 суток

Месяц принимается за 30 дней, если не требуется определить число и название месяца. Январь, март, май, июль, август, октябрь и декабрь – 31 день. Февраль в простом году – 28 дней, февраль в високосном году – 29 дней. Апрель, июнь, сентябрь, ноябрь – 30 дней.

Год представляет собой (приблизительно) то время, в течении которого Земля совершает полный оборот вокруг Солнца. Принято считать каждые три последовательных года по 365 дней, а следующий за ними четвёртый – в 366 дней. Год, содержащий в себе 366 дней, называется високосным, а годы, содержащие по 365 дней – простыми. К четвёртому году добавляют один лишний день по следующей причине. Время обращения Земли вокруг Солнца содержит в себе не ровно 365 суток, а 365 суток и 6 часов (приблизительно). Таким образом, простой год короче истинного года на 6 часов, а 4 простых года короче 4 истинных годов на 24 часа, т. е. на одни сутки. Поэтому к каждому четвёртому году добавляют одни сутки (29 февраля).

Об остальных видах величин вы узнаете по мере дальнейшего изучения различных наук.

Сокращённые наименования мер

Сокращённые наименования мер принято записывать без точки:

Меры длины Километр – км Метр – м Дециметр – дм Сантиметр – см Миллиметр – мм	Меры веса/массы тонна – т центнер – ц килограмм – кг грамм – г миллиграмм – мг
Меры площади (квадратные меры) кв. километр – км2 гектар – га кв. метр – м2 кв. сантиметр – см2 кв. миллиметр – мм2	Меры объёма (кубические меры) куб. метр – м3 куб. дециметр – дм3 куб. сантиметр – см3 куб. миллиметр – мм3
Меры времени век – в год – г месяц – м или мес неделя – н или нед сутки – с или д (день) час – ч минута – м секунда – с миллисекунда – мс	Мера вместимости сосудов

	1 мм	1 см	1 дм	1 м	1 км
	1 мм2	1 см2	1 дм2	1 м2	1 км2
	1 мм3	1 см3	1 дм3	1 м3	1 км3

Измерительные приборы

Для измерения различных величин используются специальные измерительные приборы. Одни из них очень просты и предназначены для простых измерений. К таким приборам можно отнести измерительную линейку, рулетку, измерительный цилиндр и др. Другие измерительные приборы более сложные. К таким приборам можно отнести секундомеры, термометры, электронные весы и др.

Измерительные приборы, как правило, имеют измерительную шкалу (или кратко шкалу). Это значит, что на приборе нанесены штриховые деления, и рядом с каждым штриховым делением написано соответствующее значение величины. Расстояние между двумя штрихами, возле которых написано значение величины, может быть дополнительно разделено ещё на несколько более малых делений, эти деления чаще всего не обозначены числами.

Определить, какому значению величины соответствует каждое самое малое деление, не трудно. Так, например, на рисунке ниже изображена измерительная линейка:

Цифрами 1, 2, 3, 4 и т. д. обозначены расстояния между штрихами, которые разделены на 10 одинаковых делений. Следовательно, каждое деление (расстояние между ближайшими штрихами) соответствует 1 мм. Эта величина называется

ценой деления шкалы измерительного прибора.

Перед тем как приступить к измерению величины, следует определить цену деления шкалы используемого прибора.

Для того чтобы определить цену деления, необходимо:

1. Найти два ближайших штриха шкалы, возле которых написаны значения величины.
2. Вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.

В качестве примера определим цену деления шкалы термометра, изображённого на рисунке слева.

Возьмём два штриха, около которых нанесены числовые значения измеряемой величины (температуры).

Например, штрихи с обозначениями 20 °С и 30 °С. Расстояние между этими штрихами разделено на 10 делений. Таким образом, цена каждого деления будет равна:

(30 °С – 20 °С) : 10 = 1 °С

Следовательно, термометр показывает 47 °С.

Измерять различные величины в повседневной жизни приходится постоянно каждому из нас. Например, чтобы прийти вовремя в школу или на работу, приходится измерять время, которое будет потрачено на дорогу. Метеорологи для предсказания погоды измеряют температуру, атмосферное давление, скорость ветра и т. д.

naobumium.info

это что? Средства измерения. Величины измерения

Очень часто в нашей жизни мы встречаемся со всевозможными измерениями. “Измерение” – это понятие, которое используется в различных видах деятельности человека. Далее в статье названное понятие будет рассмотрено с нескольких сторон, хотя многие считают, что оно относится конкретно к математическому действию. Однако это не совсем так. Измерительные данные используется людьми ежедневно и в различных сферах жизни, помогая выстраивать множество процессов.

Понятие измерения

Что же означает это слово и в чём заключается его суть? Измерение – это установление реального значения какой-либо величины с применением специальных средств, устройств и знаний. К примеру, необходимо выяснить, какой размер блузки нужен девушке. Для этого необходимо сантиметровой лентой измерить определённые параметры ее тела и вывести из них размер нужной одежды.

В данном случае существует несколько размерных таблиц: европейская, американская, российская и буквенная. Эта информация легко доступна, и мы не будем приводить упомянутые таблицы в нашей статье.

Скажем лишь, что ключевым моментом в данном случае является тот факт, что мы получаем определённый, конкретный размер, который был добыт путём измерения. Таким образом, любой девушке можно приобретать вещи даже не примеряя их, а просто посмотрев размерный ряд или бирку на одежде. Вполне удобно, учитывая современную работу дешёвых интернет-магазинов.

О средствах измерения

Измерение – это понятие, которое может быть использовано где угодно, и сталкиваются с ним люди практически ежедневно. Для того чтобы измерить что-то или найти какую-либо величину, используется масса различных методов. Но существует также и множество специально созданных для этих целей средств.

Средства измерения имеют свою определенную классификацию. В неё входят различные меры величин, измерительные установки, приборы, преобразователи, системы. Все они существуют для того, чтобы выявить определённую величину и максимально точно измерить её. Некоторые из названных приборов при этом осуществляют непосредственный контакт с объектом измерения.

Вообще, средства измерения можно использовать и применять только тогда, когда они предназначены для названных целей и способны сохранять единицу измерения на стабильном уровне в течение определённого времени. В противном случае результат будет неточным.

Разнообразие скорости

Также каждый день люди сталкиваются с понятием «скорость». Речь может идти о скорости транспорта, движения человека, воды, ветра и ещё массе других примеров. Однако измерение скорости для каждого из объектов происходит по-разному, с использованием абсолютно различных методов и приборов:

• такое устройство, как атмометр, предназначено для измерения скорости испарения жидкостей;
• нефоскоп измеряет направление движения и скорости облаков;
• радар определяет скорость движения транспортного средства;
• секундомер замеряет время различных процессов;
• анемометр – скорость ветра;
• вертушка позволяет уточнить скорость течения рек;
• гемокоагулограф выявляет скорость свёртывания крови человека;
• тахометр измеряет скорость и частоту вращения.

И таких примеров ещё огромное множество. Практически всё в этом мире поддаётся измерению, поэтому значение слова «измерение» настолько многогранно, что иногда трудно себе представить.

Измерения в физике

Очень многие термины и понятия тесно связаны между собой. Казалось бы, человек ежедневно занимается работой на своём рабочем месте. И измеряется она обычно в заработной плате, а также временем, потраченным на нее или другими критериями. Но существует и другое измерение работы, в данном случае – механической. Естественно, существует ещё несколько научных понятий. К ним можно отнести работу в электрической цепи, в термодинамике, кинетической энергии. Как правило, подобная работа измеряется в Джоулях, а также в эргах.

Конечно, это не единственные обозначения работы, есть и другие единицы измерения, применяемые для обозначения физических величин. Но все они принимают то или иное обозначение, в зависимости от того, какой именно процесс измеряют. Такие величины чаще всего относятся к научным знаниям – к физике. Они подробно изучаются школьниками и студентами. При желании можно заняться изучением данных понятий и величин углублённо: самостоятельно, с помощью дополнительных источников информации и ресурсов или наняв квалифицированного педагога.

Информационное измерение

Существует и такое понятие, как «измерение информации». Казалось бы, каким образом можно измерить информацию? Возможно ли такое вообще? Оказывается, вполне возможно. Зависит это только от того, что понимать под информацией. Так как определений несколько, то и способы измерения существуют различные. Измерение информации происходит в технике, в быту и в теории информации.

Единица ее измерения может выражаться в битах (самая маленькая) и байтах (более крупная). Различаются также производные от названной единицы: килобайты, мегабайты, гигабайты.

Кроме того, информацию вполне возможно измерить так же как, к примеру, энергию или вещество. Оценка информации существует в двух типах: ее измеримость (объективная оценка) и смысл (субъективная оценка). Объективная оценка информации представляет собой отказ от человеческих органов чувств, она исчисляется с помощью всевозможных датчиков, устройств, приборов, которые могут дать намного больше данных, чем человеческое восприятие.

Метод измерения

Как уже понятно из сказанного выше, измерение – это метод исследования мира в целом. Конечно, такое изучение происходит не только с помощью метода измерения, но и с помощью проведения наблюдений, экспериментов, описания. Широкий спектр наук, в которых применяется измерение, даёт возможность иметь не только конкретную информацию, но и точную. Наиболее часто данные, полученные в ходе измерения, выражаются в цифрах или математических формулах.

Таким образом, легко можно описать размеры фигур, скорости какого-либо процесса, величину и мощность какого-либо устройства. Увидев ту или иную цифру, человек легко может понять дальнейшие характеристики нужного процесса или предмета и использовать их. Все эти знания ежедневно помогают нам в обычной жизни, на работе, на улице или дома. Ведь даже простой процесс приготовления ужина задействует метод измерения.

Старинные величины

Несложно понять, что в каждой науке существуют свои величины измерения. Любой человек знает, каким образом выражаются и обозначаются секунды, минуты, часы, скорость движения автомобиля, мощность электрической лампочки и ещё много других параметров того или иного объекта. Существуют также и сложнейшие формулы, и не менее сложные в своём обозначении величины.

Как правило, такие формулы и величины измерения требуются уже более узкому кругу людей, задействованных в определённой сфере. И от владения такой информацией может зависеть очень многое.

Существует ещё м множество старинных величин, которые применялись в прошлом. Используют ли их сейчас? Конечно. Просто их переводят на современное обозначение. Найти информацию о таком процессе довольно легко. Поэтому любому человеку при необходимости не составит труда перевести, к примеру, аршины в сантиметры.

О погрешности в измерении

К сложным процессам можно также отнести классы измерений. Точнее, классы точности средств, применяемых для измерения. Это итоговые характеристики определённых приборов, показывающие степень их точности. Она определяется допускающимися пределами погрешности или иными значениями, способными влиять на уровень точности.

Довольно сложное и непонятное определение для человека, который в этом не разбирается. Однако опытного специалиста не затруднят подобные понятия. Например, необходимо измерить какую-либо величину. Для этого применяется определённое средство измерения. Показания этого средства и будут считаться результатом. Но на получение этого результата может влиять ряд факторов, в том числе и определённая погрешность. У каждого выбранного класса точности средства измерения имеется своя погрешность. Предел же допустимой погрешности просчитывается по специальной формуле.

Сферы применения знаний

Можно многое рассказать о всех тонкостях процесса измерения. И каждый сможет получить для себя новую и полезную информацию по данному вопросу. Измерение – это довольно интересный метод получения каких-либо сведений, требующий серьёзного, ответственного и качественного подхода.

Конечно, когда домохозяйка занимается приготовление пирога по специальному рецепту, измеряя в мерных стаканах необходимое количество продуктов, которые необходимы, она делает это легко. Но если вдаваться в подробности более детально, на более масштабном уровне, то нетрудно понять, что от измерительных данных зависит очень многое в нашей жизни. Выходя утром на работу, люди хотят знать, какой будет погода, как одеться, брать ли с собой зонт. И для этого человек узнаёт прогноз погоды. А ведь данные о погоде были получены тоже при помощи измерения многих показателей – влажности, температуры воздуха, атмосферного давления и т. д.

Простое и сложное

Измерение – это процесс, у которого существует масса разновидностей. Об этом было сказано выше. Получать данные можно различными путями, используя различные предметы, установки, приборы, методы. Однако приборы могут разделяться по своему назначению. Одни из них помогают контролировать, другие – выяснять у них погрешности и отклонения. Некоторые направлены на определённые каких-либо конкретных величин, которые использует человек. Полученные же данные и величины преобразовывают затем в необходимые параметры, применяя конкретный способ.

Пожалуй, самым простым измерительным прибором можно назвать линейку. С её помощью можно получить данные о длине, высоте, ширине предмета. Естественно, что это не единственный пример. Было уже сказано и о мерных стаканах. Также можно упомянуть напольные и кухонные весы. Во всяком случае, такие примеры имеются в огромном разнообразии, и наличие подобных приборов зачастую очень облегчает жизнь человека.

Измерение как целая система

Действительно, значение слова «измерение» очень велико. Сферы применения названного процесса достаточно обширны. Методов тоже огромное множество. Верным является и то утверждение, что в различных странах имеется своя система измерения и величин. Может различаться и наименование, и содержащая информация, и формулы расчёта каких-либо единиц. Наука же, которая тесно занимается учением о мерах и точном измерении, называется метрологией.

Существуют также определённые официальные документы и ГОСТы, которые контролируют величины и измерительные единицы. Множество учёных посвящали и посвящают свою деятельность изучению процесса измерения, пишут специальные книги, разрабатывают формулы, вносят свой вклад в получение новых знаний по этой теме. И каждый человек на Земле пользуется этими данными в обыденной жизни. Поэтому знания об измерении всегда остаются актуальными.

fb.ru

Измерение шестерни – штангельциркуль, зубомер.

Основные методы измерения (контроля) размера зуба зубчатых колёс — по длине общей нормали и по постоянной хорде и хорде делительной окружности. В данной статье рассмотрим различный меритель поверхностно, ещё будут подробные статьи с видео и статьи с расчётными формулами.

Самый распространённый способ измерения шестерни — по длине общей нормали штангельциркулем. Преимущество данного способа в независимости от наружного диаметра. Недостатки — трудности в замере колёс большого диаметра и колёс с большим углом наклона зубьев. При замере необходимо замерять определённое количество зубьев в обхвате:

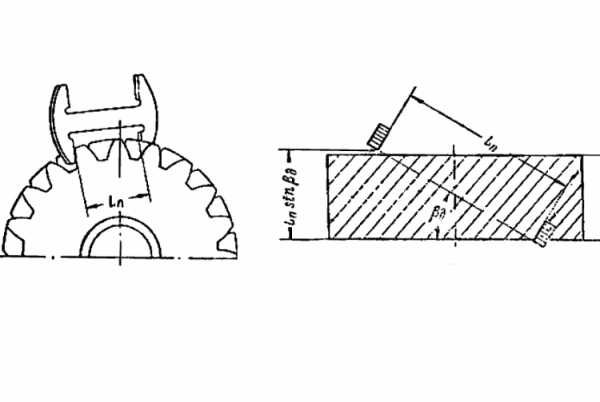
Второй способ замера по постоянной хорде и хорде делительной окружности зубомером. На определённой высоте зуба, должна быть определённая толщина. Преимущество данного способа в том что можно замерять шестерню любого диаметра и с любым наклоном. Ещё плюс в том, что при подаче под меру или чистовой не требуется ждать очень долго, как например при замере длинны общей нормали. Достаточно небольшого отрезка «чистого» зуба. Недостаток — зависимость от наружного диаметра, при изменении которого необходимо корректировать высоту замера.

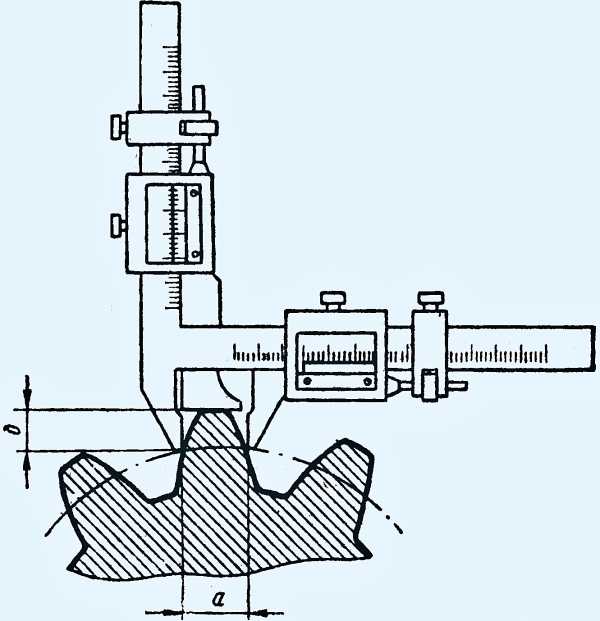
Ещё один способ, пожалуй самый «не любимый» зуборезчиками, это замер зуба шестерни тангенциальным зубомером. Тут есть и привязка к диаметру и необходимо очень правильно ставить зубомер на зуб. Данный зубомер имеет специальные ролики по модулям и индикатор.

Поделится, добавить в закладки!

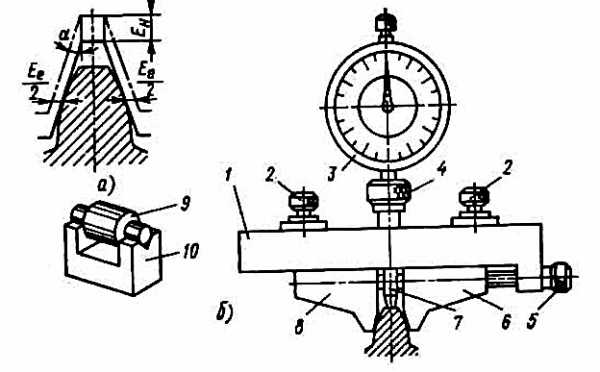
zuborez.info

Значение слова ИЗМЕРЕНИЕ. Что такое ИЗМЕРЕНИЕ?

Измерение — совокупность операций для определения отношения одной (измеряемой) величины к другой однородной величине, принятой всеми участниками за единицу, хранящуюся в техническом средстве (средстве измерений). Получившееся значение называется числовым значением измеряемой величины, числовое значение совместно с обозначением используемой единицы называется значением физической величины. Измерение физической величины опытным путём проводится с помощью различных средств измерений — мер, измерительных приборов, измерительных преобразователей, систем, установок и т. д. Измерение физической величины включает в себя несколько этапов: 1) сравнение измеряемой величины с единицей; 2) преобразование в форму, удобную для использования (различные способы индикации).

Принцип измерений — физическое явление или эффект, положенный в основу измерений.

Метод измерений — приём или совокупность приёмов сравнения измеряемой физической величины с её единицей в соответствии с реализованным принципом измерений. Метод измерений обычно обусловлен устройством средств измерений.

Характеристикой точности измерения является его погрешность или неопределённость. Примеры измерений:

В простейшем случае, прикладывая линейку с делениями к какой-либо детали, по сути сравнивают её размер с единицей, хранимой линейкой, и, произведя отсчёт, получают значение величины (длины, высоты, толщины и других параметров детали).

С помощью измерительного прибора сравнивают размер величины, преобразованной в перемещение указателя, с единицей, хранимой шкалой этого прибора, и проводят отсчёт.

В тех случаях, когда невозможно выполнить измерение (не выделена величина как физическая, или не определена единица измерений этой величины) практикуется оценивание таких величин по условным шкалам, например, Шкала Рихтера интенсивности землетрясений, Шкала Мооса — шкала твёрдости минералов.

Частным случаем измерения является сравнение без указания количественных характеристик.

Наука, предметом изучения которой являются все аспекты измерений, называется метрологией.

kartaslov.ru

Измерение – это… Что такое Измерение?

Измерение — совокупность операций для определения отношения одной (измеряемой) величины к другой однородной величине, принятой за единицу, хранящуюся в техническом средстве (средстве измерений). Получившееся значение называется числовым значением измеряемой величины, числовое значение совместно с обозначением используемой единицы называется значением физической величины. Измерение физической величины опытным путём проводится с помощью различных средств измерений — мер, измерительных приборов, измерительных преобразователей, систем, установок и т. д. Измерение физической величины включает в себя несколько этапов: 1) сравнение измеряемой величины с единицей; 2) преобразование в форму, удобную для использования (различные способы индикации).

• Принцип измерений — физическое явление или эффект, положенное в основу измерений.
• Метод измерений — приём или совокупность приёмов сравнения измеряемой физической величины с её единицей в соответствии с реализованным принципом измерений. Метод измерений обычно обусловлен устройством средств измерений.

Характеристикой точности измерения является его погрешность или неопределённость. Примеры измерений:

1. В простейшем случае, прикладывая линейку с делениями к какой-либо детали, по сути сравнивают её размер с единицей, хранимой линейкой, и, произведя отсчёт, получают значение величины (длины, высоты, толщины и других параметров детали).
2. С помощью измерительного прибора сравнивают размер величины, преобразованной в перемещение указателя, с единицей, хранимой шкалой этого прибора, и проводят отсчёт.

В тех случаях, когда невозможно выполнить измерение (не выделена величина как физическая, или не определена единица измерений этой величины) практикуется оценивание таких величин по условным шкалам, например, Шкала Рихтера интенсивности землетрясений, Шкала Мооса — шкала твёрдости минералов.

Наука, предметом изучения которой являются все аспекты измерений, называется метрологией.

Классификация измерений

По видам измерений

Согласно РМГ 29-99 «Метрология. Основыне термины и определения» выделяют следующие виды измерений:

• Прямое измерение — измерение, при котором искомое значение физической величины получают непосредственно.
• Косвенное измерение — определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной.
• Совместные измерения — проводимые одновременно измерения двух или нескольких неодноимённых величин для определения зависимости между ними.
• Совокупные измерения — проводимые одновременно измерения нескольких одноимённых величин, при которых искомые значения величин определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях.
• Равноточные измерения — ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений в одних и тех же условиях с одинаковой тщательностью.
• Неравноточные измерения — ряд измерений какой-либо величины, выполненных различающимися по точности средствами измерений и (или) в разных условиях.
• Однократное измерение — измерение, выполненное один раз.
• Многократное измерение — измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, то есть состоящее из ряда однократных измерений
• Статическое измерение — измерение физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения.
• Динамическое измерение — измерение изменяющейся по размеру физической величины.
• Абсолютное измерение — измерение, основанное на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.
• Относительное измерение — измерение отношения величины к одноименной величине, играющей роль единицы, или измерение изменения величины по отношению к одноименной величине, принимаемой за исходную.

Также стоит отметить, что в различных источниках дополнительно выделяют таки виды измерений: метрологически и технические, необходимые и избыточные и др.

По методам измерений

• Метод непосредственной оценки — метод измерений, при котором значение величины определяют непосредственно по показывающему средству измерений.
• Метод сравнения с мерой — метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой.
  • Нулевой метод измерений — метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля.
  • Метод измерений замещением — метод сравнения с мерой, в котором измеряемую величину замещают мерой с известным значением величины.
  • Метод измерений дополнением — метод сравнения с мерой, в котором значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению.
  • Дифференциальный метод измерений — метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами.

По условиям, определяющим точность результата

• Метрологические измерения
  • Измерения максимально возможной точности, достижимой при существующем уровне техники. В этот класс включены все высокоточные измерения и в первую очередь эталонные измерения, связанные с максимально возможной точностью воспроизведения установленных единиц физических величин. Сюда относятся также измерения физических констант, прежде всего универсальных, например измерение абсолютного значения ускорения свободного падения^[1].
  • Контрольно-поверочные измерения, погрешность которых с определенной вероятностью не должна превышать некоторого заданного значения. В этот класс включены измерения, выполняемые лабораториями государственного контроля (надзора) за соблюдением требований технических регламентов, а также состоянием измерительной техники и заводскими измерительными лабораториями. Эти измерения гарантируют погрешность результата с определенной вероятностью, не превышающей некоторого, заранее заданного значения^[1].
• Технические измерения, в которых погрешность результата определяется характеристиками средств измерений. Примерами технических измерений являются измерения, выполняемые в процессе производства на промышленных предприятиях, в сфере услуг и др.^[1]

По отношению к изменению измеряемой величины

Статические и динамические.

По результатам измерений

• Абсолютное измерение — измерение, основанное на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.
• Относительное измерение — измерение отношения величины к одноимённой величине, играющей роль единицы, или измерение изменения величины по отношению к одноимённой величине, принимаемой за исходную.

Классификация рядов измерений

По точности

• Равноточные измерения — однотипные результаты, получаемые при измерениях одним и тем же инструментом или им подобным по точности прибором, одним и тем же (или аналогичным) методом и в тех же условиях.
• Неравноточные измерения — измерения, произведённые в случае, когда нарушаются эти условия.

По числу измерений

• Однократное измерение — измерение выполненное один раз
• Многократное измерение — Измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, т. е. состоящее из ряда однократных измерений

Классификация измеряемых величин

По точности

• Детерминированные и случайные

По результатам измерений

• Равнорассеянные и неравнорассеянные

История

Единицы и системы измерения

См. также

Примечания

1. ↑ ^{1 2 3} Метрология и технические измерения. Колчков В. И. Ресурс «ТОЧНОСТЬ-КАЧЕСТВО»]

Литература и документация

Литература

• Кушнир Ф. В. Радиотехнические измерения: Учебник для техникумов связи. — М.: Связь, 1980
• Нефедов В. И., Хахин В. И., Битюков В. К. Метрология и радиоизмерения: Учебник для вузов. — 2006
• Пронкин Н. С. Основы метрологии: Практикум по метрологии и измерениям. — М.: Логос, 2007

Нормативно-техническая документация

• РМГ 29-99 ГСИ. Метрология. Основные термины и определения
• ГОСТ 8.207-76 ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения
• МИ 2222-92 ГСИ. Виды измерений. Классификация

Ссылки

dic.academic.ru

Что такое ден, или в чём измеряют плотность колготок

Покупая себе колготки, дамы обычно чётко представляют, какими характеристиками те должны обладать: цвет, размер и, наконец, плотность. О последней стоит рассказать подробнее, т.к. зная, например, что нужно купить колготки плотностью 40 ден, мало кто представляет, что же это такое – «ден». Многие, однако, знают, что чем больше число ден, тем толще нить, тем плотнее чулочно-носочные изделия, и, как следствие, меньше их прозрачность.
Ден (сокращение от «денье») – единица, в которой измеряется толщина волокон, или т.н. линейная плотность. Она равна отношению массы волокна к его длине. Число денье показывает, сколько весит 9000 м волокна. Почему за основу взяли именно 9 км? Ответ стоит искать в истории текстильной промышленности Европы. Развитие текстильных мануфактур и связанное с этим расширение торговли тканями привело к необходимости измерения длины и массы нитей. Одна из первых таких систем появилась во Франции, которая за несколько столетий превратилась в крупнейшего производителя шёлковых тканей. Надо отметить, что тогдашние единицы измерения сильно отличались от принятых сегодня. Так, длину нитей французы измеряли в локтях (1 фр.локоть=1,188 м), массу – в денье (1 денье=1/24 части унции, т.е. приблизительно 1,27 г). А для шёлка была создана специальная единица измерения – шёлковый титр, которая  показывала, что 9600 локтей волокна (11405 м) весят 1 денье.
В других же странах существовали свои системы мер. Отсутствие единой международной системы измерения характеристик волокон создавало определённые проблемы при осуществлении торговли пряжей, поэтому в 1900 г. в Париже состоялся международный конгресс по унификации нумерации нитей. На нём условились о переходе на метрическую систему – массу измерять в граммах, а длину – в метрах. Определили также и стандартную длину мотка – 1000 м. Для шёлка, как для пряжи, толщина которой может сильно меняться в зависимости от количества составляющих её нитей, исходя из значения французского шёлкового титра, стандартным сделали моток длиной 450 м и массой 0,05 г (т.е. 9000 м шёлковой нити должны весить 1 грамм).
Новая же единица получила название легальный титр (он же титр денье или просто денье). С тех пор денье применяется для некоторых тонких нитей (в т.ч. и шёлковых), хотя во многих странах на смену ему вскоре пришла другая единица измерения линейной плотности – текс. Он показывает массу в граммах 1 км нити. Эта единица более удобная для измерения, поэтому она и вытеснила денье. В повсеместном обращении денье остался в США.
Перевести денье в тексы и наоборот очень просто:
1ден=9*текс
1текс=1/9ден (или 0,11111111111*число ден). Например, 40 ден  равняется 4,44 текс (40/9), или 44 децитекс.

goods-info.su

Как и чем измеряются углы.

Методы и средства контроля и измерения углов



Углы и измерение углов

Угловые размеры определяют положение плоскостей, осей, линий, центров отверстий и т. д. Угловые размеры бывают зависимые и назависимые.
Независимые углы не связаны с другими параметрами изделия; зависимые углы определяются основными параметрами изделий, к которым они относятся.

В качестве единицы измерения плоских углов Международной системой единиц (СИ) принят радиан – угол между двумя радиусами круга, вырезающими на его окружности дугу, длина которой равна радиусу данного круга.
Измерение углов в радианах на практике связано с значительными трудностями, так как ни один из современных угломерных приборов не имеет градуировки в радианах.
По этой причине в машиностроении для угловых измерений в основном применяются внесистемные единицы: градус, минута и секунда. Эти единицы связаны между собой следующими соотношениями:

• 1 рад = 57°17׳45״ = 206 265″
• 1° = π/180 рад = 1,745329 × 10^-2 рад;
• 1‘ = π /10800 рад = 2,908882 × 10^-1 рад;
• 1” = π/648000 рад = 4,848137 × 10^-6 рад.

Значение угла при измерении определяют сравнением его с известным углом. Известный угол может быть задан так называемыми жесткими (с постоянным значением угла) мерами – аналогами формы элементов детали: угловыми мерами, угольниками, угловыми шаблонами, коническими калибрами, многогранными призмами.
Измеряемый угол можно сравнивать также с многозначными угломерными штриховыми мерами и различными видами круговых и секторных шкал. Еще одним методом получения известного угла является его расчет по значениям линейных размеров на основании тригонометрических зависимостей.

В соответствии с этим классификацию методов измерений углов производят в первую очередь по виду создания известного угла: сравнением с жесткой мерой, сравнением с штриховой мерой (гониометрические методы) и тригонометрическими методами (по значениям линейных размеров).

При сравнении углов с жесткой мерой отклонение измеряемого угла от угла меры определяют по просвету между соответствующими сторонами углов детали и меры, по отклонению показаний прибора линейных размеров, измеряющих несовпадение этих сторон или при контроле «по краске», т.е. по характеру тонкого, слоя краски, перенесенного с одной поверхности на другую.

В приборах для гониометрических измерений имеются штриховая угломерная шкала, указатель и устройство для определения положения сторон угла. Это устройство связано с указателем или шкалой, а измеряемая деталь – соответственно со шкалой или указателем. Определение положения сторон угла можно производить как контактным, так и бесконтактным (оптическим) способом. При соответствующих измеряемому углу положениях узлов прибора определяют угол относительного поворота шкалы и указателя.

При косвенных тригонометрических методах определяют линейные размеры сторон прямоугольного треугольника, соответствующего измеряемому углу, и по ним находят синус или тангенс этого угла (координатные измерения). В других случаях (измерение с помощью синусных или тангенсных линеек) воспроизводят прямоугольный треугольник с углом, номинально равным измеряемому, и устанавливая его как накрест лежащий с измеряемым углом, определяют линейные отклонения от параллельности стороны измеряемого угла основанию прямоугольного треугольника.

При всех методах измерений углов должно быть обеспечено измерение угла в плоскости, перпендикулярной к ребру двугранного угла. Перекосы приводят к погрешности измерения.

При наличии наклона плоскости измерения в двух направлениях погрешность измерения угла может быть и положительной и отрицательной. При измерениях малых углов эта погрешность не превысит 1% значения угла при углах наклона плоскости измерения до 8°. Такая же зависимость погрешности измерения угла от углов перекоса получается и в случаях неточного базирования деталей на синусной линейке, несовпадения направления ребра измеряемого угла или оси призмы с осью поворота на гониометрических приборах (при фиксации положения граней по автоколлиматору), при измерениях с помощью уровней и т.п.

Угол наклона плоскостей обычно определяется уклоном, численно равным тангенсу угла наклона.
Малые значения уклонов часто указывают в микрометрах на 100 мм длины, в промилле или миллиметрах на метр длины (мм/м).
Например, в мм/м указывается цена деления уровней. Пересчет уклонов в угол обычно производится по приближенной зависимости: уклон 0,01 мм/м (или 1 мкм/100 мм) соответствует углу наклона в 2″ (погрешность подсчета угла по этой зависимости составляет – 3%).

Как было показано выше в машиностроении в зависимости от используемых средств и методов различают три основных способа измерения углов:

Сравнительный метод измерения углов с помощью жестких угловых мер. При этом измерении определяется отклонение измеряемого угла от угла меры.

Абсолютный гониометрический метод измерения углов, при котором измеряемый угол определяется непосредственно по угломерной шкале прибора.

Косвенный тригонометрический метод: угол определяется расчетным путем по результатам измерения линейных размеров (катетов, гипотенузы), связанных с измеряемым углом тригонометрической функцией (синусом или тангенсом).

Сравнительный метод измерения углов обычно сочетается с косвенным тригонометрическим методом, последним определяется разница сравниваемых углов в линейных величинах на определенной длине стороны угла.

***



Угловые призматические меры и угольники

Угловые призматические меры служат для хранения и передачи единицы плоского угла. Их применяют для проверки шаблонов и угловых размеров различных изделий; для градиуровки угломерных приборов, а также для непосредственных измерений.
Угловые меры, предназначенные для проверки угломерных приборов и рабочих мер, называют образцовыми.

По точности аттестации образцовые угловые меры делят на четыре разряда (1,2,3 и 4). Предельные погрешности аттестации рабочих углов не должны превышать для угловых мер 1-го разряда – ±0,5”;   2-го разряда – ±1”;   3-го – ±3”;   4-го – ±6”.
Угловые меры собирают в блоки с помощью специальных державок.

Контроль углов угольниками осуществляют, оценивая просвет между угольником и контролируемой деталью на глаз, или сравнивают с образцовой щелью, созданной с помощью концевых мер длины и лекальной линейки.
При использовании крупных угольников просвет оценивают с помощью щупов.
Погрешность проверки углов угольником зависит от погрешности самого угольника, длины сторон угла, по которой производится проверка, и других факторов.

Угломеры с нониусами

Угломеры с нониусами применяют для измерения профиля угла на деталях контактным методом с отсчетом по угловому нониусу с точностью 2‘ и 5‘. Состоит угломер из круглого угломерного диска, скрепленного с корпусом зажимной гайкой. На основании смонтированы установочная планка и нониус с нанесенными 30 делениями с двух сторон от нулевого штриха; каждое деление соответствует 2 мин.
Линейка с лицевой стороны имеет продольный ласточкообразный паз, по которому перемешается (в процессе установки линейки на угол) хвостовик прижима.

При измерении угломер накладывают на проверяемую плоскость детали так, чтобы линейка и рабочая плоскость корпуса были совмещены со сторонами измеряемого угла. Целое число градусов отсчитывают по шкале диска до нулевого деления (штриха) нониуса. Затем определяют деление нониуса, совпадающего с делениями основной шкалы (диска).
После этого определяют по нониусу сколько минут и градусов совпадают с делениями нониуса.

Оптический угломер

В корпусе оптического угломера закреплен стеклянный диск со шкалой, имеющей деления в градусах и минутах. Цена малых делений 10 ‘. С корпусом жестко скреплена основная (неподвижная) линейка. На диске смонтированы лупа, рычаг и укреплена подвижная линейка.
Под лупой параллельно стеклянному диску расположена небольшая стеклянная пластинка, на которой нанесен указатель, ясно видимый через окуляр. Линейку можно перемещать в продольном направлении и с помощью рычага закреплять в нужном положении.

Во время поворота линейки в ту или другую сторону будет вращаться в том же направлении диск и лупа. Таким образом, определенному положению линейки будет соответствовать вполне определенное положение диска и лупы. После закрепления линеек зажимным кольцом через лупу отсчитывают показания угломера.
Оптическим угломером можно измерять углы от 0 до 180°. Допускаемые погрешности показания оптического угломера ±5‘.

Индикаторный угломер

В индикаторном угломере обычная шкала и нониус заменены индикаторным циферблатом. Отсчет угловых размеров производится по показаниям стрелки на большой шкале через 10°. Цена деления 5‘, предел измерения угломера 0…360°.

Портативный оптический угломер-шаблон

Портативный оптический угломер-шаблон предназначен для проверки профиля резцов. Он состоит из стандартной восьмикратной лупы, неподвижно закрепленной на прозрачном диске из органического стекла. Вокруг оси, запрессованной в этот диск, свободно поворачивается стальной диск, по периметру которого с высокой точностью выполнены шаблоны наиболее часто встречающихся в практике углов, радиусов и кривых. Нужный профиль шаблона накладывают на затачиваемый резец и под лупой проверяют точность доводки.
Прибор отличается точностью и удобством, так как им можно пользоваться непосредственно на рабочем месте.

***

Калибры, шаблоны и щупы



k-a-t.ru