Коэффициент теплопроводности это: Коэффициент теплопроводности – это… Что такое Коэффициент теплопроводности?

Содержание

Коэффициент теплопроводности – это… Что такое Коэффициент теплопроводности?

Теплопрово́дность — это перенос теплоты структурными частицами вещества (молекулами, атомами, электронами) в процессе их теплового движения. Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. Явление теплопроводности заключается в том, что кинетическая энергия атомов и молекул, которая определяет температуру тела, передаётся другому телу при их взаимодействии или передаётся из более нагретых областей тела к менее нагретым областям. Иногда теплопроводностью называется также количественная оценка способности конкретного вещества проводить тепло.

Исторически считалось, что передача тепловой энергии связана с перетеканием теплорода от одного тела к другому. Однако более поздние опыты, в частности, нагрев пушечных стволов при сверлении, опровергли реальность существования теплорода как самостоятельного вида материи.

Соответственно, в настоящее время считается, что явление теплопроводности обусловлено стремлением занять состояние более близкое к термодинамическому равновесию, что выражается в выравнивании температуры.

В установившемся режиме поток энергии, передающейся посредством теплопроводности, пропорционален градиенту температуры:

где — вектор потока тепла — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, — коэффициент теплопроводности (иногда называемый просто теплопроводностью), T — температура. Это выражение известно как закон теплопроводности Фурье.

В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):

где P — полная мощность тепловых потерь, S — площадь сечения параллелепипеда, ΔT

— перепад температур граней, h — длина параллелепипеда, то есть расстояние между гранями.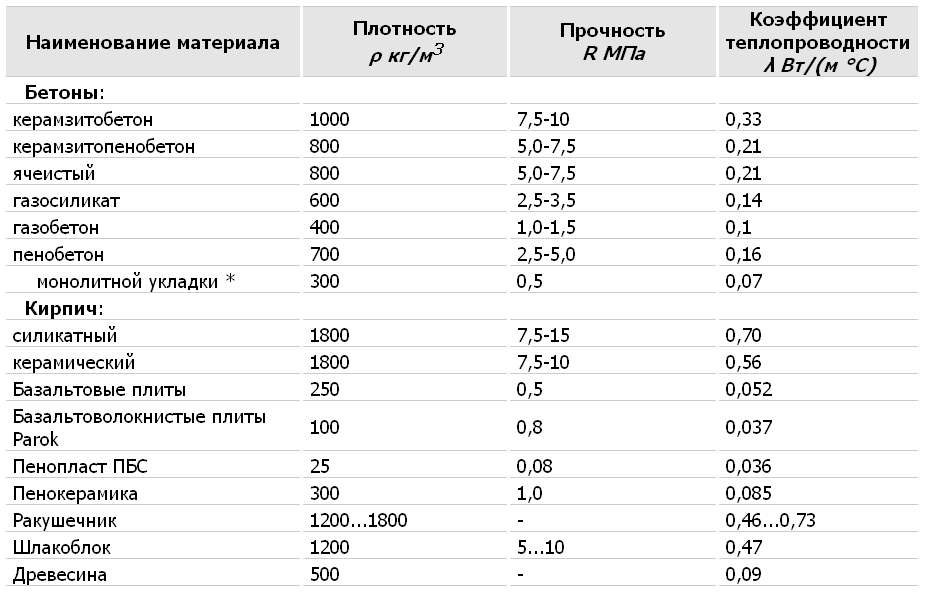

Коэффициент теплопроводности измеряется в Вт/(м·K).

Коэффициенты теплопроводности различных веществ

Материал	Теплопроводность, Вт/(м·K)
Алмаз	1001—2600
Серебро	430
Медь	382—390
Золото	320
Алюминий	202—236
Латунь	97—111
Железо	92
Платина	70
Олово	67
Сталь	47
Кварц	8
Стекло	1
Вода	0,6
Кирпич строительный	0,2—0,7
Пенобетон	0,14—0,3
Газобетон	0,1—0,3
Дерево	0,15
Шерсть	0,05
Минеральная вата	0,045
Пенополистирол	0,04
Пеноизол	0,035
Воздух (300 K, 100 кПа)	0,026
Воздух (сухой неподвижный)	0,024—0,031
Аргон	0,0177
Ксенон	0,0057
Аэрогель	0,003
Вакуум (абсолютный)	0 (строго)

На практике нужно также учитывать проводимость тепла за счет конвекции молекул и проникаемости излучений. Например, при полной нетеплопроводности вакуума, тепло может передаваться за счет излучения (пример — Солнце, установки инфракрасного излучения). А газ или жидкость могут обмениваться нагретыми или охлажденными слоями самостоятельно или искусственно (пример — фен, греющие вентиляторы).

Коэффициент теплопроводности вакуума

Коэффициент теплопроводности вакуума стремится к нулю. Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тепло в вакууме передаётся только излучением. Поэтому для уменьшения теплопотери стенки термоса делают двойными, серебрят (такая поверхность хуже излучает и лучше отражает), а воздух между ними откачивают.

Связь с электропроводностью

Связь коэффициента теплопроводности K с удельной электрической проводимостью σ в металлах устанавливает закон Видемана — Франца:

где k — постоянная Больцмана, e — заряд электрона.

Обобщения закона Фурье

Следует отметить, что закон Фурье не учитывает инерционность процесса теплопроводности, то есть в данной модели изменение температуры в какой-то точке мгновенно распространяется на всё тело. Закон Фурье не применим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т. д. Инерционность в уравнения переноса первым ввел Максвелл

[1], а в 1948 году Каттанео был предложен вариант закона Фурье с релаксационным членом:^[2]

Если время релаксации τ пренебрежимо мало, то это уравнение переходит в закон Фурье.

Примечания

↑ J. C. Maxwell, Philos. Trans. Roy. Soc. London 157 (1867) 49.
↑ C. Cattaneo, Atti Seminario Univ. Modena 3 (1948) 33.

См. также

Другие способы теплопередачи

Wikimedia Foundation. 2010.

Коэффициент теплопроводности, формула и примеры

Определение и формула коэффициента теплопроводности

Коэффициентом теплопроводности является физическая величина, которая характеризует способность вещества проводить тепло.

Обозначают коэффициент теплопроводности по-разному. Встречаются обозначения: K, и некоторые другие.

Коэффициент теплопроводности газа

В соответствии с кинетической теорией для газа коэффициент теплопроводности равен:

где — средняя скорость теплового движения молекул, — средняя длин свободного пробега молекулы, — плотность газа, — удельная теплоемкость газа в изохорном процессе.

Коэффициент теплопроводности металлов

Металлы являются хорошими проводниками тепла. Теплопроводность в металлах реализуется при помощи (в основном) посредством того, что энергию переносят свободные электроны. Коэффициент электронной теплопроводности металлов вычисляют при помощи формулы:

где — постоянная Больцмана, — концентрация электронов в металле, — длина свободного пробега, которая соответствует границе энергии Ферми () для распределения электронов по температурам при T=0K, — масса электрона, — средняя скорость свободного пробега для тех же условий, что и .

Для идеального электронного газа выражение (2) преобразуется к виду:

где — средняя длина свободного пробега, — средняя скорость теплового движения электронов.

Надо отметить, что теплопроводность, которая осуществляется кристаллической решеткой металлов существенно меньше, чем электронная. Ее можно рассчитать для кристаллов, рассматривая перемещение фотонов по кристаллу, при помощи формулы:

где с — теплоемкость единицы объема, — скорость звука, — длина свободного пробега фотона

Коэффициент теплопроводности и уравнение Фурье

Коэффициент теплопроводности входит в основное уравнение, которое описывает явление переноса тепла или уравнение Фурье. Явление теплопроводности появляется , если имеется градиент температуры. В одномерном стационарном случае уравнение Фурье можно записать как:

где помимо коэффициента теплопроводности () имеются: — количество теплоты, которое переносится через площадку в направлении, которое совпадает с направлением нормали к , в направлении уменьшения температуры, — градиент температуры. В нашем случае

Единицы измерения

Основной единицей измерения коэффициента теплопроводности в системе СИ является:

=Вт/м•К

Примеры решения задач

Расчет коэффициента теплоотдачи на плоских и гофрированных поверхностях

Во многих инженерных задачах, связанных с теплопередачей, например, при проектировании теплообменных аппаратов и радиаторов охлаждения, важное значение имеет расчет коэффициента теплоотдачи. Коэффициент теплоотдачи, который чаще всего рассчитывается с помощью эмпирических формул, характеризует интенсивность теплообмена на поверхности твердого тела. В этой статье мы расскажем и покажем, как рассчитать коэффициент теплоотдачи на плоской поверхности с помощью среды численного моделирования COMSOL Multiphysics®.

Что такое коэффициент теплоотдачи?

Рассмотрим нагретую стенку или поверхность, находящуюся в контакте с потоком жидкости. Перенос теплоты в жидкости определяется преимущественно конвекцией. {\prime \prime}— плотность теплового потока, T_w— температура стенки, а T_\infty— характерная температура жидкости.

В качестве характерной температуры жидкости могут выступать температура жидкости вдали от стенки или среднемассовая температура в трубе.

Если объект находится в неограниченно большом объеме воздуха, можно предположить, что температура воздуха вдали от поверхности объекта является постоянной и известной величиной. Такие задачи теплообмена называются внешними.

Рассмотрим пристеночную область (пусть плоскость стенки расположена по нормали к оси y, и y = 0 соответствует поверхности стенки). С учетом сделанного выше допущения очевидно, что при выполнении условия прилипания на стенке (то есть отсутствия проскальзывания) вблизи стенки образуется тонкая пленка почти неподвижной жидкости. Следовательно, перенос теплоты в этой пленке осуществляется исключительно за счет теплопроводности.

Математически этот процесс описывается уравнением [1]:

(2)

q ^{\prime \prime}
=-k\bigg(\dfrac

{\partial T}{\partial y}\bigg)_{y=0}

Здесь k— коэффициент теплопроводности жидкости, а производная от T рассчитывается в области жидкости.

Из уравнений (1) и (2) следует, что коэффициент теплоотдачи можно определить следующим образом:

(3)

h=\dfrac{-k \bigg(\dfrac{\partial T} {\partial y}
\bigg)_{y=0}}{T_w {-} T_\infty}

Расчет коэффициента теплоотдачи в COMSOL Multiphysics®

На практике измерить градиент температуры на стенке довольно затруднительно. Кроме того, хотелось бы эффективно анализировать процессы теплообмена вблизи твердой поверхности без привлечения значительных вычислительных ресурсов. Поэтому для расчета коэффициента теплоотдачи, как правило, используются неаналитические методы.

Широко признанным методом расчета коэффициента теплоотдачи является использование уравнений подобия для безразмерного числа Нуссельта. Эти уравнения позволяют быстро рассчитать коэффициент теплоотдачи для разных условий теплообмена, в том числе при свободной и вынужденной конвекции в задачах внешнего обтекания и при течении в каналах. Однако этот подход можно использовать только для объектов правильной геометрической формы: для горизонтальных и вертикальных плоских поверхностей, цилиндров и сфер.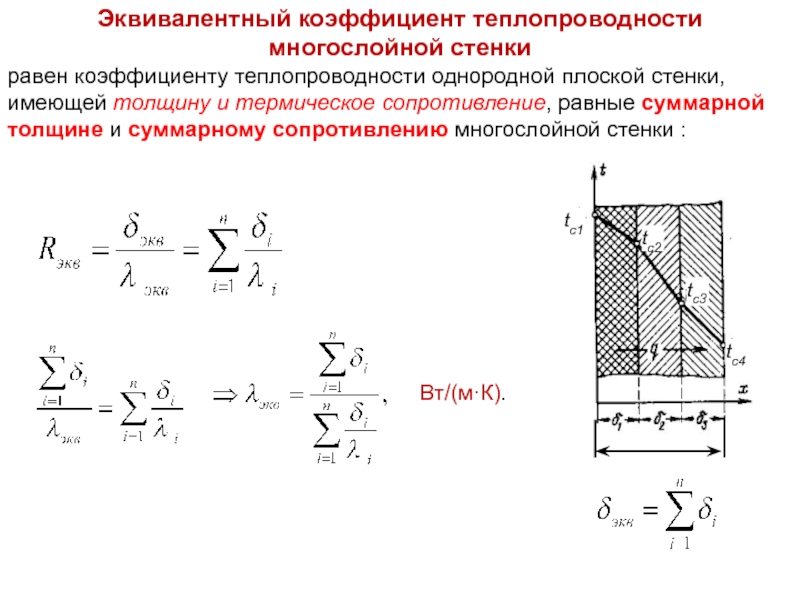

Если поверхность теплообмена в задаче имеет более сложную форму, коэффициент теплоотдачи можно рассчитать с помощью моделирования сопряженного теплообмена.

Рассмотрим эти два варианта решения задачи:

Расчет коэффициента теплоотдачи на поверхностях простой геометрической формы (например, на плоской пластине):
- Моделирование сопряженного теплообмена
- Расчетные формулы; область течения не моделируется
Вычисление коэффициента теплоотдачи на поверхностях сложной геометрической формы (например, на гофрированной пластине)

Отметим, что очень важно принимать во внимание режим течения жидкости, поскольку коэффициент теплоотдачи зависит от механизмов переноса теплоты в жидкости. В обоих случаях рассмотрим наиболее реалистичный вариант быстрого течения, например, в системе вентиляции или устройстве охлаждения электронной микросхемы. Таким образом, модель должна учитывать дополнительные механизмы переноса теплоты, обусловленные турбулентностью.

Пример 1. Теплообмен при вынужденном обтекании плоской горизонтальной пластины

Рассмотрим задачу об обтекании горизонтальной плоской пластины длиной 5 м, на которой задана постоянная плотность теплового потока 10 Вт/м². Пластина обдувается воздухом со средней скоростью 0,5 м/с и температурой 283 K. На рисунке ниже представлена схема области течения и показаны профили скорости и температуры в пределах динамического (\delta ) и температурного (\delta {T}) пограничных слоев при ламинарном режиме обтекания.

Схематическое изображение ламинарного (сверху) и турбулентного (снизу) пограничных слоев на горизонтальной пластине.

Моделирование сопряженного теплообмена

В COMSOL Multiphysics поставленную задачу можно решить численно, если воспользоваться интерфейсом Conjugate Heat Transfer (Сопряженный теплообмен), который позволяет рассчитать поля течения и температуры в жидкости. Поля скорости и давления рассчитываются в области, занятой воздухом, а поле температуры ещё и в самой пластине.

На следующем рисунке показано распределение температуры в пределах расчетной области, включающей пластину и воздух. В области течения формируются температурный и динамический погранслои, которые занимают область над пластиной толщиной около 2 см.

Распределение температуры (график скалярного поля), изотерма на 11 °C (красная линия) и поле скорости (стрелки), показывающие температурный и динамический погранслои у поверхности пластины (масштабы осей не совпадают).

По результатам моделирования можно рассчитать плотность теплового потока, если обратиться к соответствующей встроенной переменной постобработки. Если разделить найденное значение на разность температур (T_w-T_\infty), получим коэффициент теплоотдачи (уравнение 3). На графике ниже показано, как изменяется рассчитанное значение коэффициента теплоотдачи вдоль пластины.

Расчет коэффициента теплоотдачи по формулам для числа Нуссельта

Уравнение для расчета числа Нуссельта при вынужденном обтекании плоской пластины можно найти в литературных источниках (например, в [1]).

Во втором варианте расчета мы решим ту же задачу, но без моделирования области течения; то есть мы воспользуемся формулами для расчета коэффициента теплоотдачи. В этом случае расчетная область включает в себя только твердое тело (пластину). Плотность теплового потока, передаваемая с поверхности нагретой пластины холодной жидкости, задается с помощью граничного условия Heat Flux (Тепловой поток). В настройках этого граничного условия предусмотрен вариант, позволяющий задать коэффициент теплоотдачи на границе с помощью встроенных формул для расчета числа Нуссельта, как показано ниже. Еще раз отметим, что эти формулы уже имеются в COMSOL Multiphysics.

Настройки граничного условия Heat Flux (Тепловой поток).

С помощью этого условия можно рассчитать поле температуры в пластине. Зная коэффициент теплоотдачи на поверхности пластины, заданный в граничном условии Heat Flux (Тепловой поток), можно рассчитать плотность теплового потока: q=h\cdot(T_\infty-T).

Расчет коэффициента теплоотдачи

Рассчитать, как изменяется коэффициент теплоотдачи по длине пластины, можно с помощью любого из двух описанных выше методов. На рисунке ниже показано сравнение результатов расчета коэффициента теплоотдачи двумя методами.

Сравнение значений коэффициента теплоотдачи на плоской пластине, рассчитанных методом моделирования сопряженного теплообмена (синяя линия) и с помощью уравнений для числа Нуссельта (зеленая линия).

Как видно на графике, значения, полученные с помощью уравнений для числа Нуссельта, и значения, рассчитанные на основе численного моделирования сопряженного теплообмена, почти идентичны.

Интерес представляет интенсивность теплообмена на пластине, рассчитанная этими двумя методами:

Формула для расчета числа Нуссельта: 50 Вт/м
Сопряженный теплообмен: 49,884 Вт/м

В некоторых задачах эмпирические формулы для числа Нуссельта позволяют рассчитать плотность теплового потока с достаточно высокой точностью.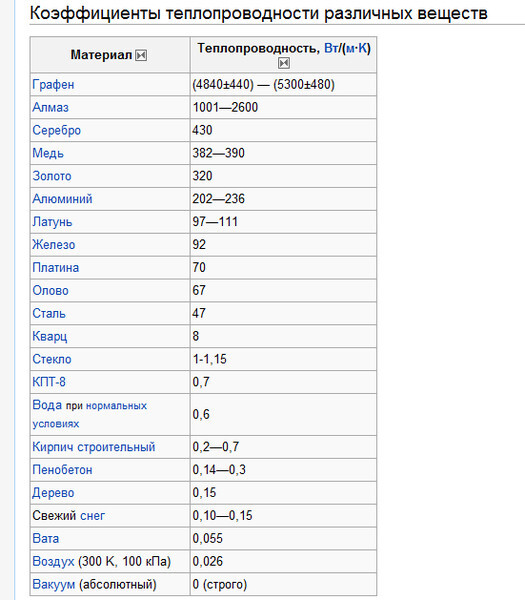 Теперь рассмотрим ситуацию, когда теплообмен происходит на поверхностии сложной формы, для которой нет формул расчета числа Нуссельта, и решить задачу можно только численно.

Пример 2. Течение у гофрированной поверхности горизонтальной пластины

Рассмотрим задачу с теми же исходными условиями, что и в первом случае, но только теперь верхняя поверхность пластины пусть будет гофрированной. На рисунке ниже представлена схема, иллюстрирующая постановку задачи. В этой модели одна из секций верхней поверхности пластины гофрирована. Остальные части пластины плоские.

Схема течения на горизонтальной пластине.

При такой форме поверхности стенки в пристеночной области появляются зоны рециркуляции, в результате чего интенсивность теплообмена повышается. На рисунке ниже представлено распределение температуры и линии тока.

Распределение температуры в градусах Цельсия (поверхность) и поле скорости (линии тока).

На графике слева показано изменение коэффициента теплоотдачи вдоль гофрированной пластины. В задачах со сложной формой поверхности теплообмена, как например при обтекании гофрированной пластины, коэффициент теплоотдачи зависит от нескольких факторов: поля температуры, поля скорости и геометрических параметров поверхности теплообмена (например, высоты гофры). Таким образом, коэффициент теплоотдачи оказывается выше, чем в случае плоской пластины (см. рисунок справа).

Изменение коэффициента теплоотдачи вдоль гофрированной пластины (слева) и вдоль плоской пластины (справа).

Для моделирования сопряженного теплообмена в моделях со сложной формой поверхностей могут потребоваться значительные вычислительные ресурсы, поэтому иногда предпочтение отдается альтернативным методам решения задачи. Хорошим вариантом решения является замена поверхности сложной формы на простую и подстановка значений коэффициента теплоотдачи, полученных на поверхности сложной формы с учетом геометрических параметров, поля скорости и разности температур. Следует отметить, что, даже если поверхность не является изотермической или если плотность теплового потока не постоянна, значение коэффициента теплоотдачи все равно представляет интерес для некоторых конфигураций, не слишком сильно отличающихся от исходной модели.

Для проверки рассмотрим простой вариант задачи о расчете коэффициента теплоотдачи на омываемой потоком гофрированной поверхности пластины. На основе полученных данных можно определить средний коэффициент теплоотдачи, который затем легко использовать в модели с плоской поверхностью пластины. Корректность такого приближенного подхода можно проверить, если проанализировать полный тепловой поток с поверхности или коэффициент теплоотдачи на основе моделирования сопряженного теплообмена.

Заключение

В этой статье мы рассказали о двух методах расчета коэффициента теплоотдачи. При моделировании сопряженного теплообмена можно использовать встроенные переменные COMSOL Multiphysics, содержащие значения плотности теплового потока. Применение граничного условия Heat Flux (Тепловой поток) и формул для расчета числа Нуссельта позволяет решать задачи о теплообмене на поверхностях простой формы. Также мы кратко обсудили, как использовать упрощенную геометрическую модель для получения данных о коэффициенте теплоотдачи на поверхностях сложной формы.

Дальнейшие шаги

Нажмите на кнопку ниже, чтобы получить дополнительную информацию о специализированных функциях моделирования теплообмена в среде численного моделирования COMSOL®.

Опробуйте рассмотренные методы с помощью учебных моделей:

Список литературы

A. Bejan et al., Heat Transfer Handbook (Справочник по теплопередаче), John Wiley & Sons, 2003.

Закон Фурье. Коэффициент теплопроводности

Содержание:

Закон Фурье. Коэффициент теплопроводности

Изотермическая поверхность делит тело на 2 зоны. 1. Температура высока в одной области, и температура низка в другой области 1. Тепло проходит через изотермическую поверхность и достигает низкотемпературной области. Количественно коэффициент теплопередачи равен плотности теплового потока. Она характеризует плотность теплового потока — это количество тепла, которое проходит через единицу поверхности за единицу времени. Y — dlf12-sec или Вт м2. Французский ученый Ж. Б. Фурье в 1807 году установил, что плотность теплового потока пропорциональна градиенту температуры.

Формула для Правила Фурье имеет знак минус, так как тепло распространяется в направлении понижения температуры, а наклон направлен в сторону ее повышения. 9 — k — hega 1. 11. 1 ОД Коэффициент пропорциональности формулы 11. 1 x равен величине w m град, называемый коэффициентом, a1 ГП-это- РЕ-1 91 Х Вт м Но Да Ноль ноль Ноль ноль Хорошо. Рисунок 11. 2. Влияние температуры на теплопроводность Теплопроводность с чаем. Теплопроводность различных веществ зависит от их физических свойств.

Передача энергии в результате обмена хаотическим, ненаправленным движением микрочастиц называется теплообменом, а количество передаваемой при этом энергии — количеством теплоты, теплотой процесса или теплотой. Людмила Фирмаль

Для конкретного тела величина теплопроводности зависит от структуры тела, его объемной массы, влажности, химического состава, давления, temperature. In в технических расчетах значение Х берется из справочной таблицы, и необходимо убедиться, что условия, при которых значение теплопроводности указано в таблице, соответствуют условиям расчетной задачи. Теплопроводность особенно зависит от температуры. Опыт показывает, что для большинства материалов эта зависимость может быть выражена в виде линейного уравнения. — о 1-Н Где ho — теплопроводность при 0 c. P-температура металла Коэффициент. Теплопроводность газов, особенно пара, во многом зависит от давления.

Численное значение теплопроводности различных веществ колеблется от 425 Вт м град серебра до очень широкого диапазона около 0, 01 Вт м град газа. Это связано с различными механизмами теплопередачи, обусловленными теплопроводностью в различных физических средах. Металл имеет самую высокую теплопроводность. Теплопроводность металлов уменьшается с повышением температуры, а также с наличием примесей и легирования elements. So, теплопроводность чистой меди составляет 390 Вт м-град, а меди, содержащей следовые количества мышьяка, -140 Вт м-град.

Передача энергии в результате макроскопического упорядоченного движения микрочастиц называется работой. Людмила Фирмаль

Теплопроводность чистого железа составляет 70 Вт м-град, 0, 5 углеродистой стали-50 Вт м град, 18 хрома и 9 никелевой легированной стали-всего 16 Вт м град. Температурная зависимость теплопроводности некоторых металлов показана ниже. Рисунок 11. 2. Теплопроводность газа низкая порядка 0, 01-1 Вт м Град, что значительно возрастает с увеличением температуры. Теплопроводность жидкостей уменьшается с увеличением температуры. Исключение составляет вода и glycerin.

Смотрите также:

Коэффициенты теплопроводности для различных материалов

122, 39, 143, 190, 193]. Большинство из них основано на измерении теплового потока и градиента температур в заданном веществе. [c.12]
Коэффициенты линейного расширения металлов и сплавов 28 Коэффициенты теплопроводности для различных материалов 30 Кузнечная сварка 140 Кристаллизация металла шва 163 Карбиды 176 [c.638]

Коэффициент теплопроводности для различных материалов неодинаков. Кроме того, для данного материала % зависит от температуры, удельного веса, влажности и в некоторой степени от давления. В таблице 2-1 даны ориентировочные значения Я, при 20° С. [c.23]

Как было сказано, коэффициент теплопроводности является физическим параметром вещества. В общем случае коэффициент теплопроводности зависит от температуры, давления и рода вещества. В большинстве случаев коэффициент теплопроводности для различных материалов определяется опытным путем. Известен ряд методов экспериментального определения коэффициента теплопроводности [Л. 189, 194, 259, 263]. Большинство из них основано на измерении теплового потока и градиента температур в заданном веществе. Коэффициент теплопроводности при этом определяется из соотношения [c.15]

Количество тепла, передаваемого в 1 час чер ез стенку площадью 1 и толщиной в 1 м при разности температур между нагреваемой и охлаждаемой сторонами в 1°С, называется коэффициентом теплопроводности. Для различных материалов колич ество тепла, передаваемого при указанных условиях, различно, следовательно,. материалы обладают различны.ми коэффициентами теплопроводности одни тела хорошо проводят тепло, другие плохо. [c.101]

Коэффициент теплопроводности является физическим параметром и зависит от химической природы вещества и его физического состояния (плотности, влажности, давления, температуры). Диапазоны изменения Л для различных материалов приведены на рис.2.1. [c.8]

Пользуясь методом регулярного режима, можно определять экспериментально коэффициенты температуропроводности различных материалов, а также и другие теплофизические параметры. Для этого проще всего создать условия нагревания или охлаждения выбранного образца материала при весьма больших критериях 5г. Такие условия сравнительно легко создать для материалов с небольшими коэффициентами теплопроводности (пористые, сыпучие материалы и пр.), помещая их (в соответствующей защит- [c.226]

Величина X оказывается весьма различной для разных материалов стенки и более или менее значительно зависит от температуры. Как показывает табл. 2-1, коэффициент теплопроводности наиболее высок у металлов, значительно ниже у неметаллических строительных материалов и достигает особенно низких значений у пористых материалов, применяемых специально для тепловой изоляции. Малая теплопроводность, т. е. хорошие изоляционные качества в последнем случае связаны с наличием пор, заполненных воздухом, теплопроводность которого весьма низка поэтому коэффициент теплопроводности пористых изоляционных материалов, как правило, тем меньше, чем ниже их объемный вес. Значения X для воздуха приведены в 2-5 (табл. 2-4). [c.96]

В металлах перенос тепла теплопроводностью в значительной мере определяется переносом энергии свободными электронами. Различия в коэффициенте теплопроводности разнообразных неоднородных материалов объясняются эффектом пористости. Для волокнистых материалов типичным нарушением однородности является анизотропия, проявляющаяся в неодинаковой теплопроводности в различных направлениях. Коэффициент теплопроводности зависит от температуры для многих металлов он уменьшается с повышением температуры по линейному закону. [c.9]

Зависимость коэффициента теплопроводности материала от его температуры. Коэффициент теплопроводности материала увеличивается с повышением его средней температуры, при которой происходит передача тепла. Для иллюстрации этого в табл. 3 приведены коэффициенты теплопроводности некоторых изоляционных материалов, определенные при различных температурах.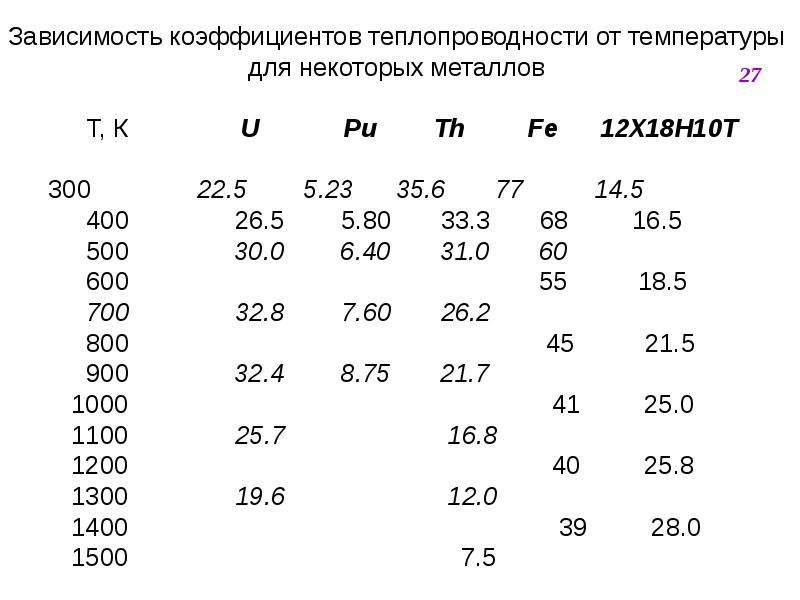 [c.27]

Так как тела могут иметь различную температуру, а при наличии теплообмена и в самом теле температура будет распределена неравномерно, то в первую очередь важно знать зависимость коэффициента теплопроводности от температуры. Опыты показывают, что для многих материалов с достаточной для практики точностью зависимость коэффициента теплопроводности от температуры можно принять линейной [c.13]

Для различных веществ коэффициент теплопроводности Я различен и в общем случае зависит от структуры, плотности, влажности, давления и температуры. Все вместе взятое сильно затрудняет выбор правильного значения коэффициента теплопроводности. Поэтому при ответственных расчетах значение коэффициента теплопроводности следует определять путем специального изучения применяемого материала. В технических же расчетах значения коэффициента теплопроводности обычно принимаются по справочным таблицам. При этом надо следить лишь за тем, чтобы физические характеристики материала (структура, плотность, влажность, температура, давление) были соответственны. Так как при распространении тепла температура в различных частях тела различна, то в первую очередь важно знать зависимость коэффициента теплопроводности от температуры. Для большого числа материалов эта зависимость оказывается почти линейной, т. е. [c.10]

Для тепловой изоляции могут применяться любые материалы с низкой теплопроводностью. Однако собственно изоляционными обычно называют такие материалы, коэффициент теплопроводности которых при температуре 50—100° С меньше 0,2 Вт/(м-°С). Многие изоляционные материалы берутся в их естественном состоянии, например асбест, слюда, дерево, пробка, опилки, торф, земля и др., но большинство их получается в результате специальной обработки естественных материалов и представляет собой различные смеси. В зависимости от технологии обработки или процентного состава отдельных компонентов теплоизоляционные свойства материалов меняются. К сыпучим изоляционным материалам почти всегда добавляются связующие материалы, которые ухудшают изоляционные свойства. [c.200]

Рис. зло. Зависимость коэффициента теплопроводности, приведенной к нулевой пористости, от диаметра областей когерентного рассеяния для различных углеродных материалов [c.111]

Для разрушающихся теплозащитных материалов характерны высокий уровень рабочих температур и существенное изменение структуры материала. Оба этих фактора сильно отражаются на теплофизических свойствах вещества. Однако если учесть степень влияния изменений различных свойств на температурное поле в материале, то прежде всего следует выделить коэффициент теплопроводности. Изменениями других теплофизических параметров в инженерной практике часто пренебрегают. Так, хотя плотность может уменьшиться почти вдвое по мере роста температуры и разложения части компонент композиционного материала, на температурное поле влияет не она сама, а произведение плотности на теплоемкость. У большинства же реальных теплозащитных материалов теплоемкость с увеличением температуры возрастает (см. приложение), и изменение произведения рс, входящего в уравнение теплопроводности, оказывается в итоге ограниченным. Как правило, оно отклоняется от первоначального значения менее чем в 2 раза. [c.75]

В задачу этого раздела не входит детальный анализ зависимости коэффициента теплопроводности от температуры для различных теплозащитных материалов, поэтому мы ограничимся лишь общими схематическими представлениями. Для сравнения будут использованы также общие сведения из теории переноса тепла в жидкостях и газах. [c.75]

Комбинируя в кладке материалы с разными коэффициентам,и теплопроводности, можно получить Кладку трех принципиально различных типов, для каждой из которых существует своя область применения. Однослойная кладка (р ис. 203, а) или кладка из нескольких слоев, коэффициенты теплопроводности которых [c.402]

Различные физические тела обладают разными значениями коэффициента теплопроводности. Кроме того, для данного вещества коэффициент теплопроводности зависит от температуры, объемного веса, влажности, структуры и в некоторой мере от давления. При технических расчетах изменением Я с температурой обычно пренебрегают и принимают в качестве расчетного значение, среднее для того интервала температур, для которого предназначен данный материал. В приложении дается таблица значений коэффициента теплопроводности X для наиболее употребительных материалов., [c.13]

Коэффициент теплопроводности X. для различных твердых материалов [c.19]

Рассмотрим пример постановки задачи нестационарного тепло-переноса. Пусть дан длинный стальной трубопровод, покрытый слоем теплоизоляции, который предназначен для транспортировки теплоносителя. Трубопровод подключен в общую сеть. Необходимо определить нестационарный тепловой режим трубопровода в период пуска теплоносителя. Исходя из поставленной практической задачи, формулируем физическую модель процесса (рис. 1 -5). Дан двухслойный полый цилиндр бесконечной длины с внутренним радиусом ri и наружным Гз. Материалы слоев стенки цилиндра различны и имеют следующие теплофизические и конструктивные параметры первый слой —Xi, Си pi, ai, 6i( i, Гг) второй слой — Хг, С2, р2, 02. 62, (Г2, з). При этом коэффициенты теплопроводности и теплоемкости материала слоев меняются с температурой по линейному закону, а плотность остается при нагревании постоянной. Начальная температура обоих слоев одинакова, постоянна и равна Гн- В начальный момент времени внутренняя поверхность цилиндра подвергается воздействию горячей среды с тем- [c.30]

Рассмотрим вначале особенности температурного поля в шиповом экране. Для шипового экрана характерно наличие нескольких разнородных материалов разной конфигурации и с различными коэффициентами теплопроводности. [c.105]

За период 1953—1960 гг. в лаборатории тепловых приборов и измерений Ленинградского института точной механики и оптики разработана группа приборов и установок, предназначенных для скоростных измерений коэффициентов теплопроводности, температуропроводности и истинной теплоемкости различных материалов. Созданные приборы и установки по принципу работы и целевому назначению могут быть разделены на две группы. [c.3]

В тех случаях, когда требуется знать температурный ход коэффициента теплопроводности полупроводниковых материалов, а также более точно определить величину измерения проводятся на установке, представленной на рис. 8. Конструкция установки построена на том же принципе, что и прибор для измерения /-a при комнатных температурах, но приведена в соответствие с условиями измерения величины коэффициента теплопроводности в вакууме при различных температурах. В этом случае резко уменьшается методическая ошибка измерения величины /-а за счет исключения тепловых потерь, обусловленных теплопроводностью воздуха и конвективным теплообменом, а потери на излучение при малых перепадах температуры на образце малы и составляют небольшую долю от теплообмена в воздухе. [c.32]

Для проверки предлагаемого метода расчета температурных полей были изготовлены клинья с углами 6°, 8°30 и —-15°. С целью получения большого количества режимов клинья изготавливались из материалов с существенно различными коэффициентами теплопроводности (использовались парафин, эпоксидная смола,свинец и цинк). Все образцы изготавливались методом литья. В каждый из клиньев по его оси на расстоянии примерно 20—30 мм друг от друга заделывались по три термопары. Спаи и проволоки термопар заливались материалом образца в момент отливки самого образца. В свинцовых и цинковых образцах термопары изолировались специальной нитью из кремнеорганического волокна, пропитанного жидким стеклом. Участки выводов термопар из тела образцов заделывались в специальные латунные трубки диаметром 4 мм. Термопары изготовлялись из константановой проволоки диаметром 0,5 мм. [c.346]

Для стены, состоящей из нескольких материалов (например, участок с теплопроводным включением), электромодель выполняется из станиолевого листа различной проводимости, что достигается путем вырезания квадратной решетки в местах меньшей проводимости так, чтобы отношения проводимостей участков модели соответствовали отношению коэффициентов теплопроводности участков образца . [c.86]

Коэффициент пропорциональности X, в формуле (10.1) имеет размерность Вт/(м К) и называется коэффициентом теплопроводности. Коэффициент теплопроводности i. для различных веществ берут из справочных таблиц. Следует иметь в виду, что А, существенно зависит от температуры. Для больщинства материалов [c.125]

Опытным путем установлено, что коэффициент теплопроводности зависит от свойств вещества (его плотности, структуры, влажности и т.п.) и параметров состояния (давления, температуры). Значения X для различных веществ и условий сводятся в соответствующие таблицы. В ответственных случаях для специфических условий их определяют непосредственно в лаборатории. Зависимость X от температуры для больщинства материалов имеет линейный характер [c.64]

Достаточно часто встречаются ситуации, когда теплопроводность к меняется в зависимости от расстояния х. Это может происходить из-за того, что тело состоит из различных материалов или теплопроводность зависит от температуры. В большинстве случаев не имеется формулы для зависимости к от х, известны лишь дискретные значения к в расчетных точках. Тогда наша задача заключается в том, чтобы получить коэффициенты расчетных точках. Для этой цели можно применить различные интерполяции. Методика, которая будет использоваться в этой книге, основана на простой физической концепции и имеет множество преимуществ. Подробное обсуждение этой темы можно найти в [5, 6]. Здесь будет дана только рекомендуемая формулировка. [c.49]

В физических лабораториях коэффициенты теплопроводности строительных материалов определяются обычно на предварительно просушенных образцах, чтобы получить сравнимые коэффициенты теплопроводности для различных материалов, исключая влияние влажности на полученные результаты. В наружных ограждениях строительные материалы всегда имеют некоторую влажность, повышающую их теплопроводность. Вследствие этого пользоваться для теплотехнических расчетов ограждающих конструкций непосредственно коэффициентами теплопроводности, полученными для сухого материала, нельзя — эти коэффициенты необходимо увеличивать.

Коэффициенты тепло-проЁодности ряда строительных материалов приведены в приложении 1. [c.27]

Вспененная теплоизоляция. Вспененная теплоизоляция имеет ячеистую структуру, образованную выделяющимся при вспенивании газом. Так как пена является неоднородным материалом, эффективная теплопроводность вспененной теплоизоляции зависит от ее объемной плотности, используемого для пенообразования газа и средней рабочей температуры. Теплопередача через вспененную изоляцию определяется конвекцией и излучением внутри ячеек и теплопроводностью твердого материала. Вакуумирование теплоизоляции является эффективным средством уменьшения ее теплопроводности, что указывает на наличие открытых ячеек в ее структуре, однако результирующие значения коэффициента теплопроводности вспененной изоляции все же значительно выше, чем у многослойной или у вакуумированной порошковой теплоизоляции. С другой стороны, диффузия атмосферных газов в ячейки может вызвать существенное повышение эффектиБного коэффициента теплопроводности.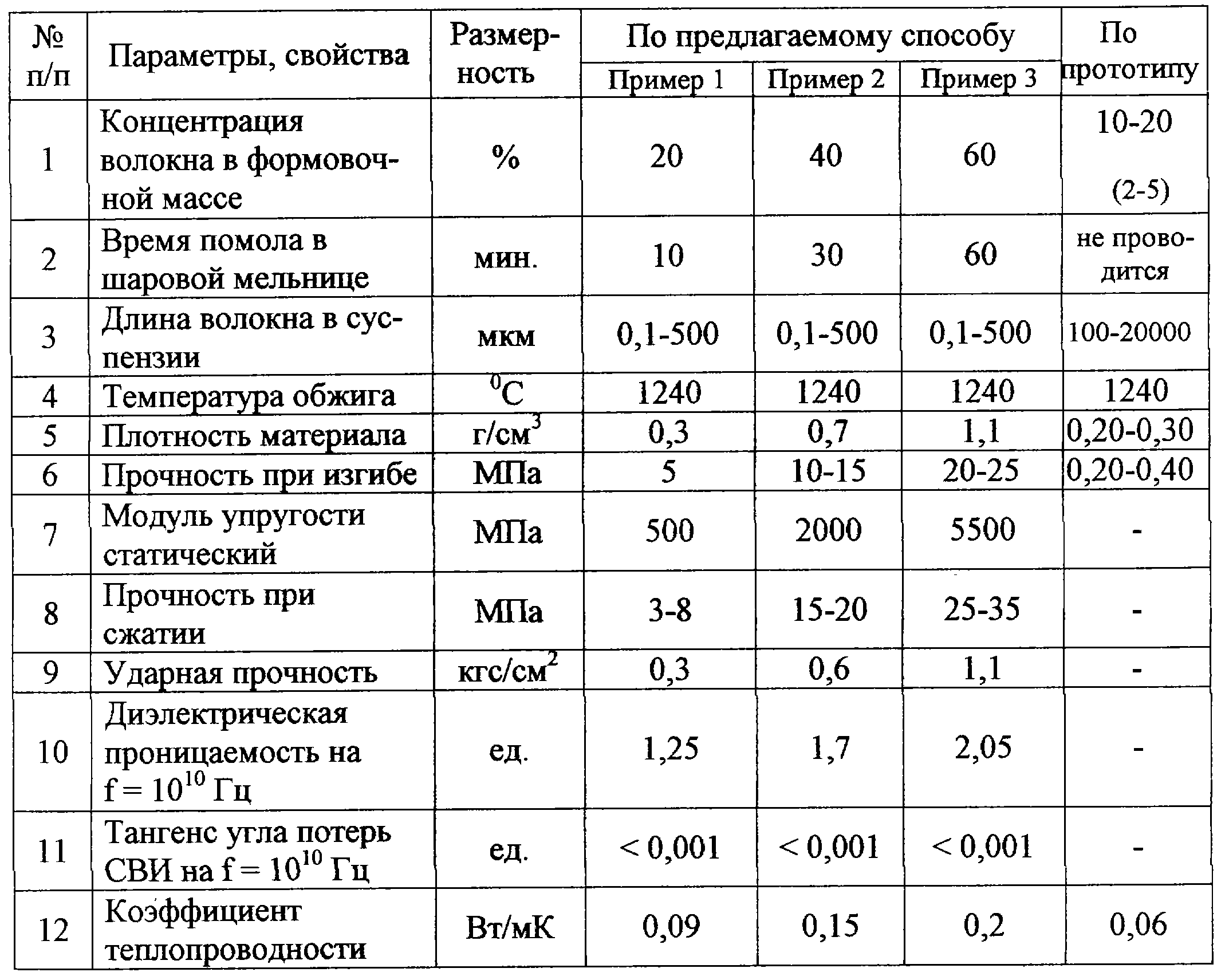 Повышение теплопроводности особенно значительно при диффузии в ячейки водорода и гелия. Данные по коэффициенту теплопроводности для различных вспененных материалов, используемых при криогенных температурах, представлены Кропшотом [60]. Из всех видов вспененной теплоизоляции. [c.44]

Коэффициент теплопроводности для большинства неметаллических твердых тел линейно изменяется с температурой. Ряд керамических веществ (окись бериллия, алюминия, двуокись титана и др.) имеет сложную температурную зависимость для коэффициента теплопроводности. Его велчина вначале падает, а затем возрастает за счет увеличения лучистого переноса тепла внутри этих тел. Указанные керамические. вещества являются твердыми диэлектриками и одновременно пористыми телами. Кроме них, многие твердые тела имеют не сплошное, а пористое или волокнистое строение Различные пористые материалы характеризуются наличием пустых промежутков (пор) между отдельными твердыми частицами. Часть этих пор представляет собой небольшие замкнутые объемы, а некоторые из них сообщаются между собой, образуя открытую пористость. Наполнителем пор может являться различная среда. Распространение тепла обусловливается совокупностью различных явлений. Внутри твердых частиц тела, а также в местах непосредственного контакта между ними тепло переносится за счет теплопроводности. В среде, заполняющей поры, перенос тепла осуществляется также теплопроводностью и, кроме того, за счет конвекции и теплового излучения. С увеличением размеров пор роль конвекции увеличивается. При уменьшении размеров пор и увеличении их количества имеет место одновременное уменьшение размеров твердых частиц, составляющих пористое тело. Это приводит к уменьшению поверхности соприкосновения между частицами, соответствующему увеличению контактного теплового сопротивления, а следовательно, уменьшению коэффициента теплопроводности. [c.9]

Наряду с изотропными материалами, для которых коэффициент теплопроводности во всех направлениях одинаков, в технике находят применение анизотропные материалы, у которых способность передавать теплоту теплопроводностью раалшша в различных направлениях. Это свойство анизотропных материалов обычно связано с особенностями их структуры (кристаллической, волокнистой, слоистой и Т.П.). В анизотропном теле угол между направлениями векторов q и grad 7 может быть меньше я, но всегда остается больше ж/2, что следует из второго закона термодинамики. Коэффициент теплопроводности для такого тела является не скаляром, как в выражении (4.3.1), а симметричным тензором второго ранга, что приводит к соответствутощему обобщению гипотезы Фурье [27, 55] [c.196]

Потери теплоты через стенку печн тем выше, чем ниже теплопроводность огнеупорного и теплоизоляционного материалов X и больше толщина стенки /. Наиболее эффективный способ снижения тепловых потерь — использование огнеупорных и теплоизоляционных материалов с низким коэффициентом теплопроводности. В табл. 5.10.1 приведены значения Я в зависимости от температуры I для различных материалов, используемых при изготовлении печей. Удельный тепловой поток от теплопроводности т равен удельному тепловому потоку от конвекции и излучения к.

и на наружной стенке печи, который может быть определен по формуле Ньютона [c.114]

В табл. 35 приведены вышеперечисленные величины и показатели для наиболее распространенных поршневых материалов. Для удобства сравнений все величины даны при нормальной температуре (20° С). С повышением температуры модуль упругости всех материалов снижается [58], [60], [61] в различной степени. Так, модуль упругости у серого чугуна СЧ-ХНММ снижается с 1,4 10 кгс/см при / = 20° С до 1,2 10 при I = 500° С, у стали 2X13 — с 2,2 10 до 1,85 10 и у сплава АК-4 — с 0,7 10 до 0,5 10 кгс/см (при повышении температуры до 300° С). Коэффициент линейного расширения увеличивается с повышением температуры для всех материалов. Так, в диапазоне температур 20—400° С для чугуна СЧ-ХНММ этот коэф–фициент возрастает с 8,9 до 14,5 10 на Г С. Изменение коэффициентов теплопроводности основных поршневых материалов приведено в табл. 36. Из таблицы видно, что у одних материалов теплопроводность с повышением температуры снижается (серые чугуны), у других повышается (алюминиевые сплавы). [c.188]

Различные исследователи дают эмпирические формулы зависимости коэффициента теплопроводности от влажности для отдельных материалов, но эти формулы применимы только для данного материала. Зависимости величин коэффициентов теплопроводности строительных материалов от их влажности для различных материалов, обработанные в виде таблиц, даны проф. А. У. Франчукам [31]. [c.27]

Экономически целесообразно не только уменьшать относительную поверхность стенок, цо и 1минимизир0вать сумму затрат на их сооружение и ремонт, а также на топливо, необходимое для покрытия потерь тепла стснками. Эти потери слагаются из тепла, отдаваемого вслед–ствие теплопроводности (95т), и тепла, аккумулируемого стенками (Qe/for). Первый вид потерь имеет место во всех печах, второй — только в печах периодического действия. Во всех случаях qti пропорционально коэффициенту теплопроводпости стенки ( ст — теплопроводность материала однослойной стенки или какого-либо ео слон, S — соответствующая толщина), а Qe/f T (с. м. гл. П1 и V)—величине( ст — удельная теплоемкость, рот—плотность материала стенки). Для различных материалов стенок значения Сст примерно одинаковы, а меньшим Лет соответствуют и меньшие рст-Для уменьшения необходимо снижение .ст, что также приводит к уменьшению Qe/f (такой же эффект вызывает и понижение рст). [c.16]

При трении фрикционного материала по металлам с различными значениями коэффициента теплопроводности Я в той паре, в которой металл обладает большим коэффициентом теплопроводности, поверхностная температура будет меньше, а температурный градиент во фрикционном материале — больше. Для этой пары значения коэффициента трения и износостойкость будут соответственно выше. На фиг. 327 показано изменение износостойкости вальцованной ленты 6КВ-10 при трении в одинаковых условиях по металлическим элементам, имеющим различную теплопроводность. Так, точка А получена при трении по стали 55ЛП, точка Б — по чугуну СЧ 15-32, а точка В — по биметаллическому шкиву, имеющему металлизированный слой, состоящий из 50% стали 10 и 50% Си.

[c.551]

Для поперечно-обтекаемых пучков труб до последнего времени не было достаточно данных ни для введения температурного критерия, ни для обоснованного выбора определяющей температуры, которая в неявном виде учла бы влияние температурных условий. Поэтому различные авторы, располагая, по существу, одними и теми же экспериментальными материалами, приходили к различным выводам. Так, например, при составлении норм теплового расчета котельных агрегатов ЦКТИ издания 1945 г. (Л. 2] и ВТИ издания 1952 г. [Л. 3] на основе анализа экспериментальных работ по теплоотдаче В. М. Антуфьева и Л. С. Козаченко [Л. 33], Н. В. Кузнецова и В. А. Локшина [Л. 34] и ряда других даны различные рекомендации по выбору определяющей температуры в нормах ЦКТИ в качестве таковой принимается температура стенки, а в нормах ВТИ физические константы в критериях Nu и Re рекомендовано определять по различным температурам, причем коэффициент теплопроводности определяется по более высокой из температур потока и стенки, коэффициент вязкости — по более низкой, а удельный вес у или плотность р — по температуре потока. [c.63]

С. Создаются автоматизированные установки для измерения коэффициента теплопроводности сыпучих, волокнистых и пористых теплоизоляционных материалов в интервале температур от—120 до 1300° С при различных давлениях газа-наполнителя, для измерения коэффициента температуропроводности металлов в интервале от —100 до 1100°С и для импульсных динамических измерений истинной теплоемкости металлов в интервале 20—1100° С. Теоретическое обос- [c.5]

Предлагаемый способ решения задач по теплопроводности позволил разработать целый ряд методов и создать приборы экспрессного комплексного определения в одном опыте теплофизичеюких коэффициентов различных материалов, действующие в условиях нестационарного температурного поля. Решены задачи для двухслойных сред. [c.186]

Текстолит, ДСП (древесно-слоистый пластик) и прессованную древесину используют в подшипниках для тяжелого машиностроения. Полимерные самосмазывающиеся материалы на основе полиамидов, полиацетилена, политетрафторэтилена и различных смол используют для подшипников, ра ающих в температурном диапазоне 200.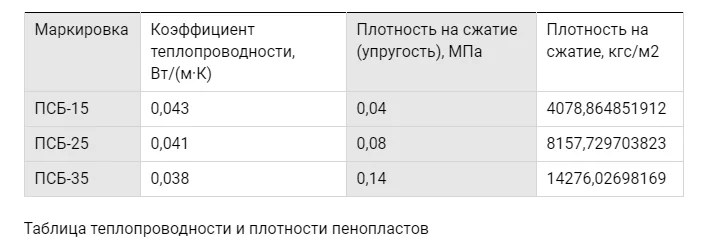 .. + 280°С при значительных скоростях скольжения. Фторопласты (полимеры и сополимеры галогенопроизводных, этилена и пропилена) обладают хорошими антифрикционными свойствами, химической инертностью, но высоким коэффициентом линейного расширения и низким коэффициентом теплопроводности. Подшипники с резиновыми вкладышами хорошо работают с водяной смазкой. [c.464]

Особенности теплового расчета углеграфитовой теплообменной аппаратуры, а также справочные данные по коэффициентам линейного расширения, теплопроводности и теплопередачи для различных марок фафита приведены в монофафиях [18, 23]. Расчет основных элементов теплообменников на прочность производят по ГОСТ 14249. При этом нужно учитывать, что модуль упругости фафитовых материалов примерно на два порядка ниже, чем для углеродистых сталей, а временное сопротивление меньше в 30 раз. [c.392]

Коэффициенты теплопроводности, теплообмена и теплопередачи

При известных значениях коэффициента теплопроводности материала стенки теплообменного элемента и его толщины б рассчитывают коэффициент теплопередачи /с,, от слоя к хладагенту через стенку теплообменника [c.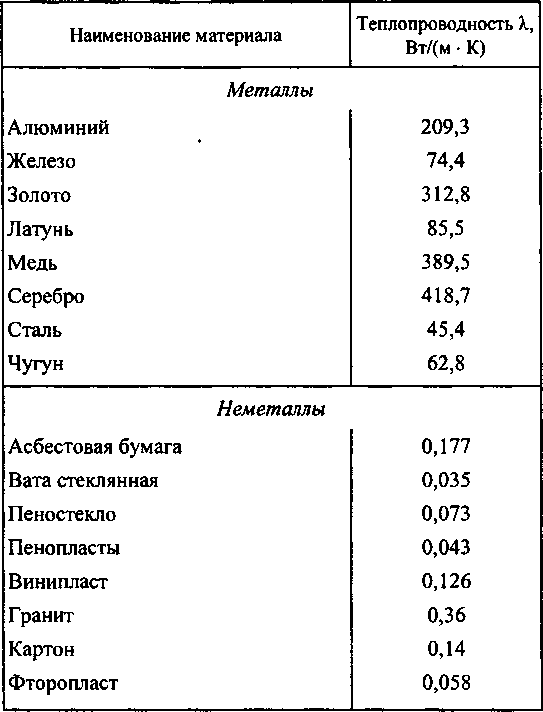 264]

Для вычисления коэффициента теплопередачи или термического сопротивления плоской стенки необходимо определить коэффициенты теплоотдачи и теплопроводности. В табл. 57 и 58 приведены коэффициенты теплопроводности некоторых металлов, а также осадков и загрязнений теплообменных холодильных аппаратов. [c.311]

При исследовании переноса тепла в зернистом слое можно пользоваться как коэффициентом теплопередачи, так и эффективным коэффициентом теплопроводности слоя. В первом случае теплообмен определяется разностью температур между потоком и стенкой, являющейся границей слоя. [c.57]

Уравнения материального и теплового баланса с эмпирическими коэффициентами массо- и теплопередачи повсеместно применяются при расчете гетерогенно-каталитических процессов, скорость которых лимитируется диффузией реагентов к поверхности частицы катализатора и теплообменом между потоком и активной поверхностью. Строго говоря, использование эффективных коэффициентов обосновано только когда поверхность катализатора равнодоступна (см. п. 2). Более тонкие эффекты могут определяться явлениями термодиффузии и диффузионной теплопроводности, возникающими при наложении и взаимном влиянии процессов тепло- и массопереноса, а также изменением физических свойств пограничного слоя, а следовательно и значений коэффициентов диффузии и температуропроводности в результате химических превращений. Ошибка, допускаемая в результате пренебрежения этими явлениями, в условиях большинства химических реакций мала. В некоторых процессах значительную роль играет так называемый стефановский поток, возникающий вследствие неравной скорости диффузии исходных веществ и продуктов реакции или изменения объема в ходе химических превращений. Влияние стефановского потока на скорость химической реакции рассматривается в п. 2. [c.116]

Высокие коэффициенты теплопроводности и теплоотдачи являются положительными качествами холодильных агентов, так как это улучшает работу теплообменных аппаратов (испарителя и конденсатора), повышая интенсивность теплопередачи. [c.37]

Очистка теплообменных аппаратов. При использовании теплоносителей, выделяющих осадки и оказывающих коррозионное действие на аппаратуру, поверхность теплообмена покрывается слоем Загрязнений, обладающих низкой теплопроводностью, что снижает коэффициент теплопередачи. Очистку аппаратов от загрязнений производят периодически. Продолжительность работы между очистками зависит от допускаемой степени загрязнения и от скорости загрязнения поверхности теплообмена и может колебаться от нескольких дней до нескольких месяцев (и более). [c.440]

Примечание. В формулах приняты следующие обозначения а— коэффициент температуропроводности, м-/ч -Х—коэффициент теплопроводности, Вт/Чм- С) ср-тепло-емкость газа при постоянном давлении, Дж/(кг °С) —средняя движущая сила теплопередачи, °С ДС—движущая спла массопередачи, выраженная в единицах концентрации (кг м , моль/м ) О—количество перенесенной массы, кг р — количество перенесенной теплоты, Дж Г—межфазная поверхность, эквивалентная поверхности теплообмена, м= т—время работы аппарата, с, ч р—плотность, кг/м” О—коэффициент молекулярной диффузии, м/с —общий коэффициент теплоцередачи, Вт/(м °С) а — частный коэффициент теплоотдачи, Вт/(м – С) гОр—линейная скорость потока, м/с I — характерный линейный размер, м —кинематический коэффициент вязкости газа, м с К—общий коэффициент массопередачи, кг/(м- ч) б—коэффициент массопередачи, м/ч [прп теплообмене—кг/(м ч)] —инерционно-вязкостный критерий (видоизмененный критерий Рейнольдса для газа).

[c.90]

Значения коэффициента теплопроводности указанных загрязнений во много раз ниже коэффициента теплопроводности стальной стенки аппарата (А, 50 Вт/(м-К), поэтому термическое сопротивление стенки заметно увеличивается при наличии на ней даже тонкого слоя загрязнений. Увеличение термического сопротивления стенки из-за загрязнений, имеющихся на ней, существенно ухудшает теплопередачу интенсивных теплообменных аппаратов, таких как конденсаторы с водяным охлаждением, испарители для охлаждения жидкостей, льдогенераторы и т. п. Поверхности теплообменных аппаратов следует периодически очищать от загрязнений, а в некоторых случаях вести непрерывную фильтрацию протекающей жидкой среды. [c.534]

Значения коэффициента теплопроводности указанных загрязнений во много раз ниже коэффициента теплопроводности стальной стенки аппарата [Я, 50 Вт/(м-К)], поэтому термическое сопротивление стенки заметно увеличивается при наличии на ней даже тонкого слоя загрязнений. Увеличение термического сопротивления стенки из-за загрязнений, имеющихся на ней, существенно ухудшает теплопередачу интенсивных теплообменных аппаратов (конденсаторы с водяным охлаждением, испарители для охлаждения жидкостей, льдогенераторы и т. д.). [c.62]

Коэффициенты теплоотдачи. При низких коэффициентах теплоотдачи приходится увеличивать поверхность теплопередачи, что делает теплообменные аппараты дорогими и громоздкими, С увеличением теплопроводности, плотности, теплоемкости и с уменьшением вязкости хладагентов коэффициент теплоотдачи а, Вт/(м -К), увеличивается (при одинаковой скорости). [c.30]

Если по трубе выходит в атмосферу пар, образовавшийся при испарении низкотемпературной жидкости, то приток тепла по этой трубе к жидкости заметно снижается. Это относится, в частности, к горловине сосудов Дьюара. Теплопередача по трубе, через которую выходит пар, может быть рассчитана при двух допущениях 1) между паром и стенкой трубы имеет место идеальный теплообмен, их температуры равны между собой в любом сечении 2) коэффициент теплопроводности материала трубы линейно зависит от температуры. [c.395]

При охлаждении в теплообменной аппаратуре горячей воды холодной коэффициент теплоотдачи от горячей поверхности к углеграфитовому материалу имеет тот же порядок величин, что и ог его внутренней поверхности к холодной воде — 520— 1400 Вт/(м -К). При использовании в качестве теплоносителя водяного пара коэффициент теплоотдачи от пара к углеграфитовой стенке в несколько раз больше, чем в предыдущем случае, и составляет (в зависимости от скорости пара) 2800—10500 Вт/(м–К). Высокие значения коэффициента теплоотдачи от теплоносителей к стенке углеграфита и его теплопроводности обеспечивают коэффициенты теплопередачи в углеграфитовых теплообменниках от 1400 до 11700 Вт/(м2.К). [c.104]

Общий коэффициент теплопередачи, как известно, находится в прямой зависимости от теплопроводности материала и в обратной зависимости от толщины стенки теплообменных элементов. Однако во многих случаях из-за высоких давлений тепло-обменные элементы вынуждены изготавливать толстостенными многослойными из материалов с низкой теплопроводностью , что в значительной мере усложняет конструкцию и иногда приводит к ошибочным решениям и авариям. Это особенно важно учитывать при разработке и эксплуатации теплообменных элементов, работающих в коррозионных средах. Большинство неметаллических материалов, применяемых для антикоррозионных покрытий поверхностей теплопередачи, обладают весьма низкой теплопроводностью. Сравнительно незначительные изменения толщины антикоррозионного слоя, нанесенного на металлическую поверхность, вызывают резкое снижение общего коэффициента теплопередачи и могут быть причиной опасных нарушений технологического режима. Вместе с тем, неудовлетворительная антикоррозионная защита теплообменной поверхности может приводить к преждевременному разрушению теплообменных элементов и опасным последствиям, связанным с образованием взрывоопасных сред. [c.182]

Значение этого коэффициента показывает, насколько легко тепло может передаваться из одной среды в другую в данном теплообменнике. А это в свою очередь зависит от препятствующего теплообмену сопротивления, создаваемого средами и материалом поверхностей теплообмена.

Полное сопротивление (величина, обратная общему коэффициенту теплопередачи или теплопроводности) равно [c.172]

Величина Яэка = где б — толщина прослойки жидкости (газа), заключенной между двумя стенками К — коэффициент теплопередачи через стенки и прослойку между ними. Отношение к обычному коэффициенту теплопроводности А, отражает влияние конвекции на теплообмен и носит название коэффициента конвекции вц. Таким образом, причем при Ог- Рг [c.287]

При изучении теплопередачи развитых поверхностей в большинстве случаев удобно раздельно рассматривать перенос тепла тепловровод-ностью внутри ребра и теплообмен с окружающей средой на поверхности. Обычно это конвективный или лучистый теплообмен либо оба вида теплообмена, действующие совместно. Могут быть и другие случаи. Например, если на полое ребро из материала с низким коэффициентом теплопроводности с одной стороны падает лучистый тепловой поток от источника с высокой температурой, при анализе необходимо наряду с теплопроводностью учитывать внутренний лучистый теплообмен. [c.14]

Основным показателем, характеризующим работу испарителей, является коэффициент теплопередачи, который характеризует величину теплового потока, передаваемого через 1 м теплообменной поверхности при температурном напоре в 1 °С. Величина коэффициента теплопередачи зависит от многих факторов от теплофизических свойств теплооб-менивающихся веществ коэффициента теплопроводности материала [c.105]

Теплопередача в аппаратах с мешалкой. Конструктивно теплообменные элементы могут быть выполнены в виде рубашки или змеевика. Теплоотдача от рубашек к среде р.чссчитывается по уравнению Nu = 0,4 ргО.зз а в случае змеевика Ыи = 1,01 Ке -( х/цст) – Здесь Ыи = а01Х Яе — пс1-/ -, Рг = ЦСр/Х а — коэффициент теплоотдачи X — коэффициент теплопроводности V, 1 — кинематическая и динамическая вязкость жидкости Ср — удельная теплоемкость —динамическая вязкость жидкости при температуре стенки. [c.33]

Особенности теплового расчета углефа-фитовой теплообменной аппаратуры, а также справочные данные по коэффициентам линейного расширения, теплопроводности и теплопередачи для различных марок фафита приведены в монофафиях [18, 23]. Расчет основных элементов теплообменников на прочность производят по ГОСТ 14249. При этом нужно учитывать, что модуль упругости фафитовых материалов примерно на два порядка ниже, чем для углеродистых сталей, а временное сопротивление меньше в 30 раз. [c.392]

При расчете воздушных прослоек между двумя поверхностями наличие конвекции увеличивает теплопередачу по сравнению с теплопередачей теплопроводностью через воздух. При расчете таких прослоек их принято тем не менее считать на теплопроводность, но увеличивать коэффициент теплопроводности по сравнению с действительным на величину ф = где — теплопроводность, учитывающая конвекцию, а — теплопроводность неподвижного воздуха, Об за-ботка опытных данных по теплообмену в различных прослойках позволила Крауссольду предложить для них следующие критериальные уравнения [c.43]

В теплопередаче существенное значение имеют загрязнения и осадки, образующиеся в процессе эксплуатации теплообменных аппаратов. В расчетах можно принимать следующие значения коэффициентов теплопроводности осадков и загрязнений (ккал1м час °С) [c.136]

Закон теплопроводности для жидкостей и газов такой же как и для твердых тел, только значения к в этом случае сравнительно малы. Так, например, при комнатной температуре значение й (ккал1час-м °С) составляет для неподвижной воды0,506, а для подвижного воздуха — 0,022, в то время как для меди к = = 330, а для 01Гнеупорного кирпича к = I. Коэффициенты теплопроводности расплавленных металлов [18] и растворов солей значительно выше, чем воды. В большинстве промышленных теплообменников, работающих с принудительной конвекцией жидкостей, теплопередача конвекцией существенно превышает передачу тепла теплопроводностью, следовательно, такие задачи не могут быть решены только при помощи таблиц теплопроводности жидкостей. Конвективный теплообмен рассмотрен в последующих главах. Однако при ламинарном течении вязких масел в трубах действие конвекции невелико и теплопроводность в этом случае играет основную роль. Через прозрачные газы, такие, как воздух, тепло может передаваться теплопроводностью, конвекцией и излучением. [c.47]

В контактных аппаратах с неподвижным катализатором Нельзя применять водяные холодильники, так как вследствие весьма низкой теплопроводности пористых гранул ванадиевого катализатора [порядка 0,57 ккал м-град -ч) у теплообменных поверхностей происходит резкое-падение температуры ниже температуры зажигания катализатора. Кроме того, на холодных поверхностях теплообменных труб может конденсироваться серная кислота, что вызывает быструю их коррозию и порчу контактной массы, находящейся в зоне теплообменников. Эффективная теплопроводность кипящего с лоя достигает 15 ООО ккал/(д1 грй 9.ч) [181, а коэффициенты теплоотдачи столь велики [16, 19], что становится возможным применение водяных холодильников (см. главу IV). При этом не происходит конденсации серной кислоты на холодных поверхностях, омываемых кипящим слоем при снижении температуры до 390° С, т. е. ниже рабочих температур катализа [20]. Теплопередача от кипящего слоя к воде, протекающей в трубах водяного холодильника, происходит много интенсивнее, чем в газовых теплообменниках, которые устанавливают между слоями аппаратов с неподвижным катализатором коэффициент теплопередачи возрастает в среднем в 15 раз. Движущая сила процесса теплопередачи Ai (разность температур) также увеличивается примерно в 2 райа. Таким образом, площадь теплообмена Р, вычисляемая по формуле [c.144]

Основное влияние на эффективность теплообмена в СВ (см. таблицу) при охлаждении как коксового газа, так и воздуха оказьшает скорость газа. Оценивая влияние на теплообмен физических свойств газа, заметим, что абсолютные значения объемных коэффициентов теплопередачи на коксовом газе выше, чем на воздухе. Это можно объяснить преоблад щим влиянием различной теплопроводности и вязкости газов. Теплопроводность коксового газа в семь раз вьппе, а вязкость вдвое меньше, чем у воздуха. Поэтому при менее интенсивной гидродинамической обстановке в аппарате, работающем на коксовом газе, эффективность теплообмена выше. [c.8]

Помимо конвекции, теплопередача в слое происходит по двум путям—теплопроводностью и излучением между нагретыми частицами топлива. Теплопроводность в контактах, путем непосредственного соприкосновения частиц, как показали опыты, очень ма.ла [436]. Играет роль главным образом стуненчатый теплообмен— от частицы к частице излучением и конвекцией, а по частице теплопроводностью. В предыдущих работах, папример, Майерса [40i], Терреса и др. [475], теплопроводность и излучение между частицами не разделялись, либо учитывались параллельно. Ирактически тенлонроводность и излучение между частицами, дсшствителт.но, трудно отделить, поскольку они взаимно связаны, хотя и управляются разными законами. В вашей работе [371] теплопроводность и излучение учитывались также суммарно. В последующих работах [160, 240 сделан вывод формулы для определения коэффициента лучистого теилообмена между кусками топлива и суммарного коэффициотгта излучения (радиации) и теплопроводности в слое с учетом термического сопротивления теплопроводности частиц. [c.439]

Анализ системы, состоящей из уравнения (2.44) и кинетического уравнения реакции первого порядка, проведен в работах [96, 97]. Такой подход удобно использовать для моделирования процессов получения крупногабаритных блоков, так как часто из-за низкой теплопроводности режим их получения близок к адиабатическому (число БиоСО, ). Более полная постановка задачи моделирования процесса химического формования в форме дается анализом режимов работы периодического реактора без смешения при нестационарно протекающих химических процессах и кондуктивном теплопереносе. Один из вариантов расчета может быть выполнен при следующих допущениях [98] реакция, протекающая в рассматриваемой области, является одностадийной и необратимой теплопередача в зоне реакции осуществляется путем теплопроводности движение реагирующего вещества и связанный с ним конвективный механизм передачи тепла отсутствуют исходное вещество и продукты реакции находятся в одном фазовом состоянии, т. е. протекание реакции не сопровождается фазовыми превращениями лраиица рассматриваемой области непроницаема для вещества теплообмен на границе раздела происходит по закону Ньютона величины, характеризующие физические свойства вещества (теплопроводность, теплоемкость, плотность), химическую реакцию (энергия активации, предэкспоненциальный фактор, тепловой эффект) и условия протекания процесса (давление, температура окружающей среды, форма и размеры области, коэффициент теплоотдачи), в ходе процесса не изменяются. [c.54]

Часто теплообменную аппаратуру, рассчитанную на определенные среды, используют для других сред не всегда учитывают тот факт, что коэффициент теплоотдачи между стенкой и теплоносителем снижается с уменьшением вязкости, теплопроводности, плотности и теплоемкости теплоносителя иногда не принимается во внимание изменение температуры, приводящее, в свою очередь, к изменению физических свойств теплоносителя и соответственно коэффициента теплопередачи. Допускаются ошибки при расчете скоростей теплоносителей. Снижение скорости теплоносителя приводит к ламинарному движению пограничного слоя, повышению теплового сопротивления потока и резкому снижению коэффициента теплоотдачи. Не всегда правильно выбираются конфигурации и размеры теплообменной аппаратуры, существенно изменяющие формы поверхности теплопередачи. При выборе или замене теплообменной аппаратуры должны учитываться, кроме величины поверхности теплопереда- [c.181]

Интенсификация процессов второй группы осуществляется ускорением теплопередачи. Количество тепла, передаваемое в единицу времени от реакционной массы к теплоносителю чере 1 стенки теплообменного элемента, пря.мо пропорционально произведению разности температур на коэффициент теплопередачи. Коэффициент теплопередачи является функцией теплопроводности пленок теплоносителя и реакционной массы на на-ружтюй и внутренней повер.хности стенки теилообменного элемента (тепловое сопротивление самой стенкн обычно невелико и не оказывает существенного влияния на интенсивность теплообмена).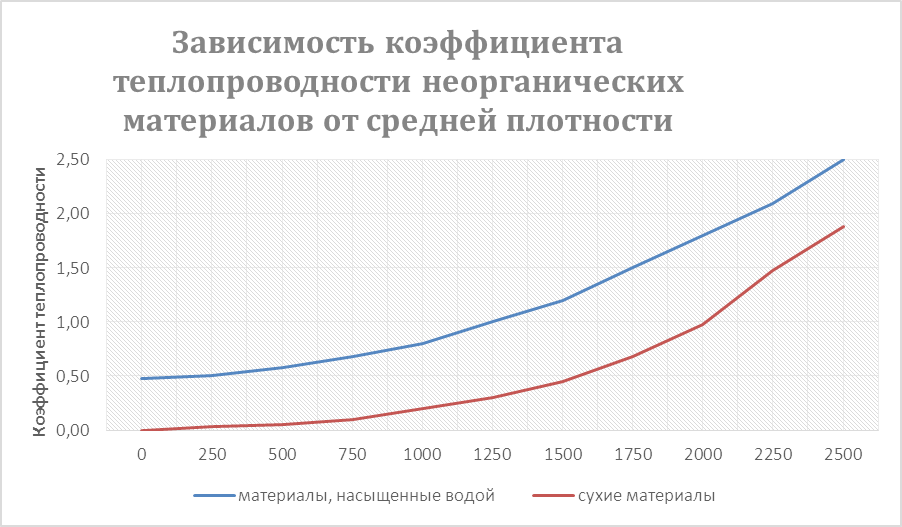 Следовательно, для интенсификации теплопередачи [c.303]

При применении первого и второго методов конверсии углеводородов водяным паром генераторы являются адиабатическими реакторами, в которых газовые компоненты взаимодействуют на поверхности неподвижной насадки или кокса. По третьему методу реакция проводится при температурах, достигающих 900″, и теплообмен между топочными газами, с одной стороны, и реагирующими газами и катализатором, с другой стороны, происходит через стенки металлических труб диаметром до 200 мм. Коэффициент теплопередачи в этом случае достаточно высок, поскольку коэффициент теплоотдачи от топочных газов к металлической стенке велик благодаря лучеиспусканию пламени. Кроме того, теплопроводность металлической стенки очень хорошая, и только низкий коэффициент теплоот- [c.109]

При эксплуатации теплообменных аппаратов в кипящем слое иногда наблюдается интенсивное осаждение твердых частиц на поверхности теплоо бменника. Это явление происходит в результате электризации частиц, осмоления поверхности и т. п. Поэтому пренебрегать термическим сопротивлением теплопроводности, как это иногда делают, при определении коэффициента теплопередачи не следует. Это тем более недопустимо, что в условиях кипящего слоя коэффициент имеет большие значения. [c.105]

Физические свойства ожижающего агента оказывают определенное влияние на теплообмен. Наиболее существенную роль играет теплопроводность газа (жидкости) К, с ,Вт/(м граддс) ростом которой увеличивается коэффициент теплоотдачи а. Некоторые зависимости влияния температуры слоя на теплопередачу приведены на рис. 12 [18]. [c.29]

Уравнение (3) для определения коэффициента теплоперадачи было получено в предположении [25], что сопротивление теплообмену между кипянщм слоем и окружающей его стенкой определяется в основном поверхностным слоем, прилегающем к стенке. Такого рода явления наблюдаются в однофазном потоке [6]. Было сделано предположение [25], что толщина поверхностной пленки зависит от кинематической вязкости газа и вертикальной составляющей скорости частиц. Хотя отдельные положения Лева и его соавторов вызывают сомнение [16], общий подход к определению зависимости коэффициента теплопередачи при помощи уравнения (3) является шагом вперед с точки зрения полного учета влияния всех переменных. В рассмотрение введены теплопроводность и плотность газа, которые не учитывались в уравнении (2). [c.31]

В этих уравнениях общий коэффициент теплопередачи относится к полной поверхности на стороне того или другого теплоносителя, включающей поверхность оребрения Лет соответствует средней величине основной поверхности, несущей оребре-ние (например, поверхности разграничивающих листов в пластинчатом теплообменнике) и T o характеризуют эффективность (к. п. д.) сребренной поверхности, включающей и основную поверхность, на стороне горячего и холодного потоков соответственно, т. е. поверхностей A . и Лх Ог и Ох—коэффициенты теплоотдачи, которые являются сложными функциями геометрии поверхности, свойств потока и условий течения. Кроме того, в уравнениях (1-2) фигурируют толщина стенки основной поверхности Ь и теплопроводность ее Хст- Наиболее сложно определение значений коэффициентов теплоотдачи а, особенно для поверхностей со сложной геометрией соответствующие расчетные уравнения или графики приводятся при рассмотрении отдельных типов развитых теплообменных поверхностей. [c.10]

Не удается найти страницу | Autodesk Knowledge Network

(* {{l10n_strings.REQUIRED_FIELD}})

{{l10n_strings.CREATE_NEW_COLLECTION}}*

{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}

{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings. TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$select.selected.display}}
{{article.content_lang.display}}
{{l10n_strings.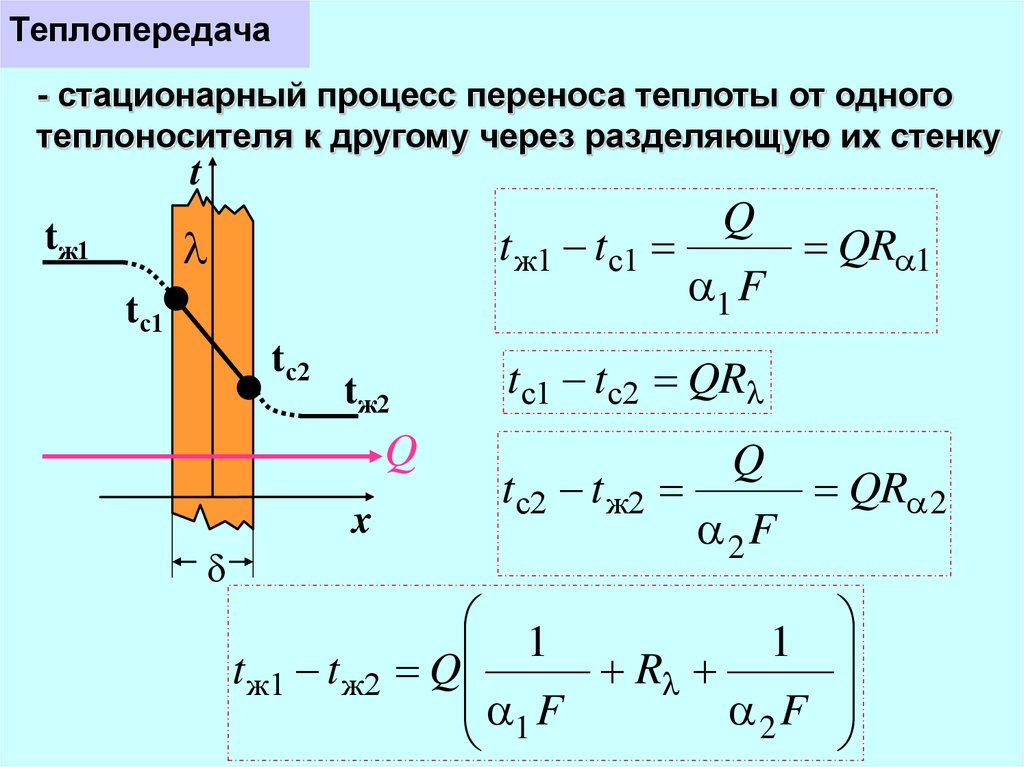 AUTHOR}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}
Теплопроводность металлов и сплавов
В этой статье представлены данные теплопроводности для ряда металлов и сплавов. Теплопроводность измеряет способность материала пропускать тепло через проводимость.
Теплопроводность измеряет способность материала пропускать тепло через проводимость. Теплопроводность материала сильно зависит от состава и структуры.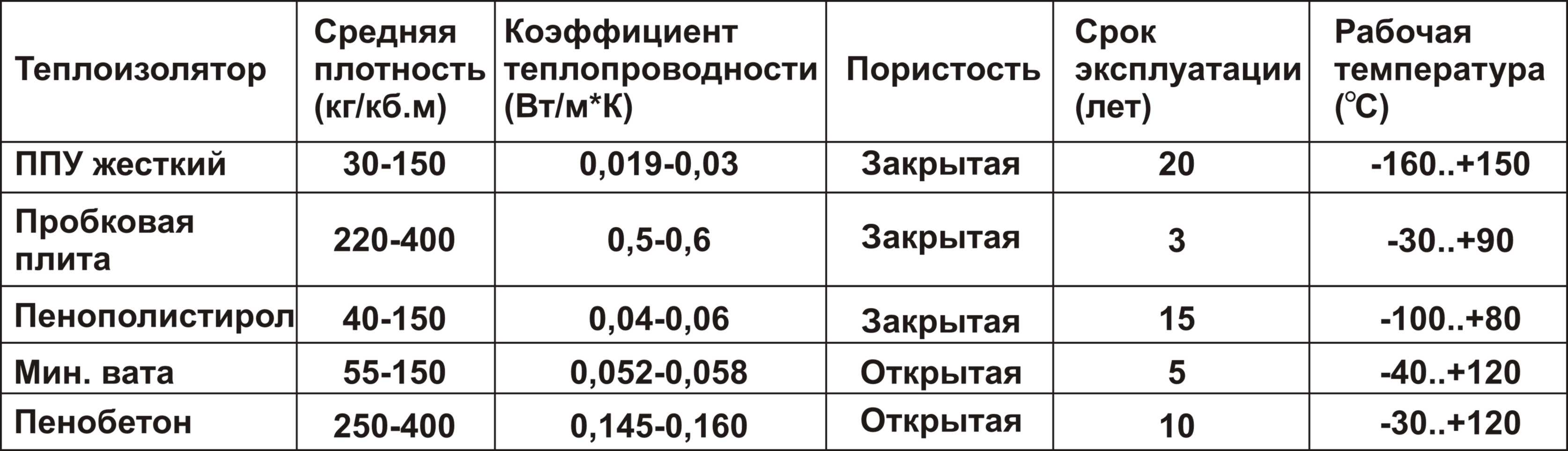 Вообще говоря, плотные материалы, такие как металлы и камень, являются хорошими проводниками тепла, в то время как вещества с низкой плотностью, такие как газ и пористая изоляция, плохо проводят тепло.
Теплопроводность материалов требуется для анализа сетей теплового сопротивления при изучении теплопередачи в системе.
Дополнительную информацию см. В статье «Значения теплопроводности для других распространенных материалов».
В следующих таблицах показана теплопроводность некоторых металлов и сплавов при различных температурах.
Материал Температура Теплопроводность Температура Теплопроводность
Адмиралтейство Латунь 20 96.1 68 55,5
100 103,55 212 59,8
238 116,44 460 67,3
Алюминий 20 225 68 130
100 218 212 126
371 192 700 111
Сурьма 20 18.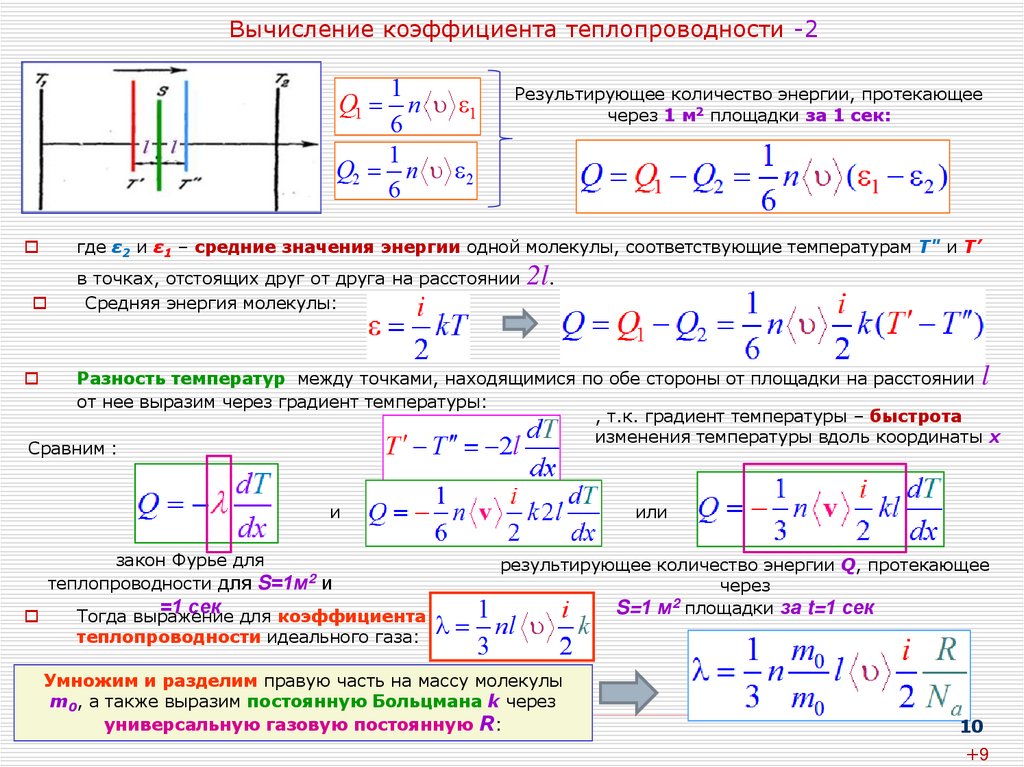 3 68 10,6
100 16,8 212 9,69
Бериллий 20 139 68 80,1
100 212 76,2
371 109 700 63,0
Латунь -165 106 -265 61,0
20 144 68 83.0
182 177 360 102
Бронза 20 189 68 109
Cadmiuim 20 92,8 68 53,6
100 90,3 212 52,2
Медь 20 401 68 232
100 377 212 218
371 367 700 212
Золото 20 317 68 183
Германий 20 58. 8 68 34,0
Инконель X -3 13,2 27 7,62
20 13,7 68 7,90
577 25,5 1070 14,7
Железо 20 71,9 68 41,6
100 65,7 212 38,0
371 44.6 700 25,8
Чугун (кованый) 20 60,4 68 34,9
100 59,9 212 34,6
Чугун (литье) 53 48,0 127 27,7
Свинец 0 35,1 32 20,3
20 34,8 68 20.1
260 30,3 500 17,5
Магний 20 170 68 98,5
100 167 212 96,3
188 163 370 93,9
Молибден 0 137 32 79,0
20 136 68 78. 4
427 115 800 66,7
Монель -250 20,73 -418 11,98
20 27,5 68 15,86
800 46,9 1472 27,1
Никель 20 62,4 68 36,0
100 58.0 212 33,5
293 47,5 560 27,4
Палладий 20 67,5 68 39,0
Платина 20 71,0 900 68 41,0
100 70,6 212 40,8
427 69,2 800 40,0
Плутоний 20 8.65 68 5,00
Родий 20 152 68 88,0
Серебро 20 419 68 242
100 405 212 234
316 366 600 211
Сталь, 1% углерода 20 45,3 68 26. 2
100 44,8 212 25,9
SS ANSI 301, 302, 303, 304 35 14,0 95 8,08
100 15,0 212 8,69
900 28,0 1652 16,2
SS ANSI 310 0 11,9 32 6,85
20 12.3 68 7,11
900 32,0 1652 18,5
SS ANSI 314 30 17,3 86 10,0
100 17,6 212 10,2
300 18,4 572 10,6
900 22,6 1652 13,1
SS ANSI 316 -50 13.0 -58 7,51
20 13,9 68 8,04
950 26,1 1742 15,1
SS ANSI 321, 347, 348 – 70 14,3 -94 8,25
20 15,7 68 9,06
900 29,4 1652 17,0
SS ANSI 403, 410, 416 , 420 -70 26. 0 -94 15,0
20 26,0 68 15,0
1000 26,0 1832 15,0
SS ANSI 430 50 21,8 122 12,6
900 25,0 1652 14,4
SS ANSI 440 100 22,1 212 12.8
500 27,5 932 15,9
SS ANSI 446 0 22,4 32 13,0
20 22,7 68 13,1
1000 38,0 1832 22,0
SS ANSI 501, 502 30 37,0 86 21,4
100 36.2 212 20,9
830 27,8 1526 16,0
Тантал 20 55,0 68 31,8
Таллий 0 50 32 29,0
Торий 20 29,4 68 17,0
100 30,5 212 17.6
299 33,3 570 19,3
Олово 20 62,1 68 35,9
100 58,8 212 33,9
Титан 20 15,6 68 9,00
100 15,3 212 8,86
299 14.7 570 8,50
Вольфрам 20 159 68 92,0
100 154 212 89,2
299 142 570 82,0
Уран 20 24,2 68 14,0
100 26,0 212 15,0
770 40.6 1418 23,4
Ванадий 20 34,6 68 20,0
Цинк 20 112 68 64,9
100 111 212 63,9
Цирконий 0 19,0 32 11,0
Статья Создана: 5 ноября 2013 г.
1
Лабросс, С.Тепловая и магнитная эволюция ядра Земли. Phys. Планета Земля. Интер. 140 , 127–143 (2003)
ADS Статья Google ученый
2
Стейси, Ф. Д. и Лопер, Д. Э. Пересмотренная оценка проводимости железного сплава при высоком давлении и ее значение для баланса энергии ядра. Phys. Планета Земля. Интер. 161 , 13–18 (2007)
ADS CAS Статья Google ученый
3
Ниммо, Ф.в Трактат по геофизике 2-е изд. (ред. Шуберт Г.) 27–55 , 201–219 (Elsevier, 2015)
Статья Google ученый
4
Ша, X. и Коэн, Р. Исследования из первых принципов удельного электрического сопротивления железа под давлением. J. Phys. Конденс. Дело 23 , 075401 (2011)
ADS PubMed Статья CAS Google ученый
5
Gomi, H.и другие. Высокая проводимость железа и тепловая эволюция ядра Земли. Phys. Планета Земля. Интер. 224 , 88–103 (2013)
ADS CAS Статья Google ученый
6
Поццо М., Дэвис К., Габбинс Д. и Алф Д. Тепловая и электрическая проводимость железа в условиях ядра Земли. Природа 485 , 355–358 (2012)
ADS CAS PubMed PubMed Central Статья Google ученый
7
де Кокер, Н., Steinle-Neumann, G. & Vlcek, V. Электросопротивление и теплопроводность жидких сплавов Fe при высоких P и T, а также тепловой поток в ядре Земли. Proc. Natl Acad. Sci. США 109 , 4070–4073 (2012)
ADS CAS PubMed Статья Google ученый
8
Олсон, П. Новый основной парадокс. Наука 342 , 431–432 (2013)
ADS CAS PubMed Статья PubMed Central Google ученый
9
Ниммо, Ф.в Трактат по геофизике (ред. Шуберт Г.) 31–65 , 217–241 (Elsevier, 2007)
Google ученый
10
Тардуно, Дж. А., Коттрелл, Р. Д., Дэвис, У. Дж., Ниммо, Ф. и Боно, Р. К. Геодинамо от Хаде до Палеоархея, зарегистрированное с помощью одиночных кристаллов циркона. Наука 349 , 521–524 (2015)
ADS CAS PubMed Статья Google ученый
11
McWilliams, R.С., Конопкова, З. и Гончаров, А. Ф. Метод мгновенного нагрева для измерения теплопроводности при высоком давлении и температуре: применение к Pt. Phys. Планета Земля. Интер. 247 , 17–26 (2015)
ADS CAS Статья Google ученый
12
Мак-Вильямс, Р. С., Далтон, Д. А., Конопкова, З., Махмуд, М. Ф. и Гончаров, А. Ф. Измерения непрозрачности и проводимости благородных газов в условиях планетных и звездных недр. Proc. Natl Acad. Sci. США 112 , 7925–7930 (2015)
ADS CAS PubMed Статья PubMed Central Google ученый
13
Стейси, Ф. Д. и Андерсон, О. Л. Электрическая и теплопроводность сплава Fe-Ni-Si в условиях сердечника. Phys. Планета Земля. Интер. 124 , 153–162 (2001)
ADS CAS Статья Google ученый
14
Сигл, К.Т., Коттрелл, Э., Фей, Ю. В., Хаммер, Д. Р., Пракапенка, В. Б. Электрические и теплопередающие свойства железа и сплава железо-кремний при высоком давлении. Geophys. Res. Lett. 40 , 5377–5381 (2013)
ADS CAS Статья Google ученый
15
Би Й., Тан Х. и Цзин Ф. Электропроводность железа при ударном сжатии до 200 ГПа. J. Phys. Конденс. Дело 14 , 10849 (2002)
ADS CAS Статья Google ученый
16
Киллер, Р.Н. и Ройс, Э. Б. в Physics of High Energy Density Vol. 48 (ред. Caldirola, P. & Knoepfel, H.) 106–125 (Academic Press, 1971)
Google ученый
17
Franz, R. & Wiedemann, G. Ueber die Wärme-Leitungsfähigkeit der Metalle. Ann. Phys. 165 , 497–531 (1853)
Артикул Google ученый
18
Анзеллини, С., Деваэле, А., Мезуар, М., Лубейр, П. и Морард, Г. Плавление железа на внутренней границе ядра Земли на основе быстрой дифракции рентгеновских лучей. Наука 340 , 464–466 (2013)
ADS CAS PubMed Статья Google ученый
19
Бёлер Р. Температуры в ядре Земли по результатам измерений температуры плавления железа при высоких статических давлениях. Природа 363 , 534–536 (1993)
ADS CAS Статья Google ученый
20
Комабаяши Т., Фей, Ю., Менг, Ю. и Пракапенка, В. Измерения дифракции рентгеновских лучей на месте перехода γ-ε границы железа в ячейке с алмазной наковальней с внутренним нагревом. Планета Земля. Sci. Lett. 282 , 252–257 (2009)
ADS CAS Статья Google ученый
21
Денг, Л., Сигл, К., Фей, Ю. и Шахар, А. Удельное электрическое сопротивление железа при высоком давлении и температуре и последствия для ядер планет. Geophys. Res. Lett. 40 , 33–37 (2013)
ADS CAS Статья Google ученый
22
Джексон, Дж. М. и др. Плавление сжатого железа путем мониторинга атомной динамики. Планета Земля. Sci. Lett. 362 , 143–150 (2013)
ADS CAS Статья Google ученый
23
Ривольдини А., Ван Хоолст Т.И Верхувен, О. Внутренняя структура Меркурия и содержание серы в его ядре. Икар 201 , 12–30 (2009)
ADS CAS Статья Google ученый
24
Хо, К. Ю., Пауэлл, Р. У. и Лили, П. Е. Теплопроводность элементов. J. Phys. Chem. Ref. Данные 1 , 279–422 (1972)
ADS CAS Статья Google ученый
25
Hauck, S.А., Домбард А. Дж., Филлипс Р. Дж. И Соломон С. С. Внутренняя и тектоническая эволюция Меркурия. Планета Земля. Sci. Lett. 222 , 713–728 (2004)
ADS CAS Статья Google ученый
26
Конопкова З., Лазор П., Гончаров А. Ф., Стружкин В. В. Теплопроводность ГПУ-железа при высоком давлении и температуре. High Press. Res. 31 , 228–236 (2011)
ADS Статья CAS Google ученый
27
Дубровинский, Л.С., Саксена, С. К., Тутти, Ф., Рехи, С. и ЛеБехан, Т. Рентгеновское исследование теплового расширения и фазового перехода железа при многомегабарном давлении на месте. Phys. Rev. Lett. 84 , 1720–1723 (2000)
ADS CAS PubMed Статья PubMed Central Google ученый
28
Секко Р. А. и Шлёссин Х. Х. Удельное электрическое сопротивление твердого и жидкого Fe при давлениях до 7 ГПа. Дж.Geophys. Res. Твердая Земля 94 , 5887–5894 (1989)
Артикул Google ученый
29
Ниммо Ф. и Стивенсон Д. Дж. Влияние ранней тектоники плит на тепловую эволюцию и магнитное поле Марса. J. Geophys. Res. Планеты 105 , 11969–11979 (2000)
ADS Статья Google ученый
30
Монтойя, Дж.А., Гончаров, А.Ф. Расчет с помощью метода конечных элементов зависимых от времени тепловых потоков в ячейке с алмазной наковальней, нагретой лазером. J. Appl. Phys. 111 , 112617 (2012)
ADS Статья CAS Google ученый
31
Johannsen, P. G. Показатель преломления галогенидов щелочных металлов. 1. Модель постоянной совместной плотности состояний. Phys. Ред. B 55 , 6856–6864 (1997)
ADS CAS Статья Google ученый
32
Гримсдич, М., Letoullec, R., Polian, A. & Gauthier, M. Определение показателя преломления в ячейках с алмазной наковальней: результаты для аргона. J. Appl. Phys. 60 , 3479–3481 (1986)
ADS CAS Статья Google ученый
33
Chen, B. et al. Упругость, прочность и показатель преломления аргона при высоких давлениях. Phys. Ред. B 81 , 144110 (2010)
ADS Статья CAS Google ученый
34
Деваэле, А.и другие. Квазигидростатическое уравнение состояния железа выше 2 Мбар. Phys. Rev. Lett. 97 , 215504 (2006)
ADS PubMed Статья CAS PubMed Central Google ученый
35
Sommerfeld, A. Zur Elektronentheorie der Metalle auf Grund der Fermischen Statistik. Z. Phys. 47 , 1–32 (1928)
ADS CAS МАТЕМАТИКА Статья Google ученый
36
Паркер, В.Дж., Дженкинс, Р. Дж., Эбботт, Г. Л. и Батлер, К. П. Флэш-метод определения температуропроводности, теплоемкости и теплопроводности. J. Appl. Phys. 32 , 1679 (1961)
ADS CAS Статья Google ученый
37
Татено С., Хиросе К., Охиси Ю. и Тацуми Ю. Структура железа во внутреннем ядре Земли. Наука 330 , 359–361 (2010)
ADS CAS Статья Google ученый
38
Шен, Г., Пракапенка, В. Б., Риверс, М. Л., Саттон, С. Р. Структура жидкого железа при давлениях до 58 ГПа. Phys. Rev. Lett. 92 , 185701 (2004)
ADS PubMed Статья CAS PubMed Central Google ученый
39
Гончаров А.Ф. и др. Дифракция рентгеновских лучей в ячейке с алмазной наковальней, нагретой импульсным лазером. Rev. Sci. Instrum. 81 , 113902 (2010)
ADS PubMed Статья CAS PubMed Central Google ученый
40
Росс, Р.Г., Андерссон, П., Сундквист, Б., Бэкстрем, Г. Теплопроводность твердых тел и жидкостей под давлением. Rep. Prog. Phys. 47 , 1347 (1984)
ADS CAS Статья Google ученый
41
Болин Л. Теплопроводность металлов при высоком давлении. Solid State Commun. 19 , 389–390 (1976)
ADS CAS Статья Google ученый
42
Шарма, С.К. Температура Дебая ГПУ-железа при экстремальном сжатии. Solid State Commun. 149 , 2207–2209 (2009)
ADS CAS Статья Google ученый
43
Дубровинский, Л. С., Саксена, С. К., Дубровинская, Н. А., Рехи, С. и Ле Бихан, Т. Грюнайзен Параметр ε-железа до 300 ГПа по данным рентгеновского исследования на месте. Am. Минеральная. 85 , 386–389 (2000)
ADS CAS Статья Google ученый
44
Van Zytveld, J.Удельное электрическое сопротивление жидких переходных металлов. J. Phys. Coll. 41 , C8-503-C8-506 (1980)
Google ученый
45
Френч, М. и Маттссон, Т. Р. Термоэлектрические транспортные свойства молибдена на основе моделирования ab-initio. Phys. Ред. B 90 , 165113 (2014)
ADS Статья CAS Google ученый
46
Киттель, К. Введение в физику твердого тела 8-е изд. (John Wiley & Sons, 2005)
47
Панеро В. Р. и Жанло Р. Градиенты температуры в нагреваемой лазером ячейке с алмазной наковальней. J. Geophys. Res. Твердая Земля 106 , 6493–6498 (2001)
Артикул Google ученый
48
Кифер, Б. и Даффи, Т. С. Моделирование методом конечных элементов нагреваемой лазером ячейки с алмазной наковальней. Дж.Прил. Phys. 97 , 114902 (2005)
ADS Статья CAS Google ученый
49
Гончаров А.Ф. и др. Теплопроводность аргона при высоких давлениях и высоких температурах. J. Appl. Phys. 111 , 112609 (2012)
ADS Статья CAS Google ученый
50
Beck, P. et al. Измерение температуропроводности при высоком давлении с использованием метода нестационарного нагрева. Заявл. Phys. Lett. 91 , 181914 (2007)
ADS Статья CAS Google ученый
51
Yamazaki, D. et al. Уравнение состояния P-V-T для ε-железа до 80 ГПа и 1900 K с использованием аппарата высокого давления типа Kawai, оснащенного спеченными алмазными наковальнями. Geophys. Res. Lett. 39 , L20308 (2012)
ADS Google ученый
52
Хиросе, К., Labrosse, S. & Hernlund, J. Состав и состояние ядра. Annu. Преподобный “Планета Земля”. Sci. 41 , 657–691 (2013)
ADS CAS Статья Google ученый
Теплопроводность высокопрочного полиэтиленового волокна и приложения для криогенного использования
Локальное повышение температуры ленты является одной из нестабильностей высокотемпературных сверхпроводящих (ВТСП) катушек с кондуктивным охлаждением.Чтобы предотвратить локальное повышение температуры ВТСП-ленты, на катушку катушки или прокладку для отвода тепла с ВТСП-ленты был нанесен армированный волокном пластик с высокой теплопроводностью. Теплопроводность волокон рами увеличивается за счет увеличения ориентации молекулярных цепей при втягивании воды и уменьшается за счет разрыва цепи при облучении γ -лучами или мостиковыми точками в молекулярных цепях при парофазной обработке формальдегидом. Теплопроводность высокопрочного волокна из полиэтилена (ПЭ) со сверхвысокой молекулярной массой (UHMW) линейно возрастает пропорционально модулю упругости и уменьшается за счет разрывов молекулярных цепей при облучении γ -лучами.Этот результат свидетельствует о влиянии длинных протяженных молекулярных цепей из-за высокой молекулярной массы на высокую теплопроводность высокопрочного волокна из сверхвысокомолекулярного полиэтилена. Теплопроводность высокопрочных пластиков из сверхвысокомолекулярного полиэтилена, армированного волокном, параллельно направлению волокон пропорциональна коэффициенту поперечного сечения арматуры, ориентированной в направлении проводимости. Эффект отвода тепла от высокопрочного полиэтилена, армированного волокном UHMW, из ленты HTS выше, чем у стеклопластика (GFRP), и ниже, чем у нитрида алюминия (AlN).В случае HTS-катушки термостойкость, намотанная на бобину катушки, сделанную из высокопрочного полиэтилена, армированного волокном UHMW, такая же, как у AlN, и лучше, чем у GFRP.
1. Введение
При применении полимерных материалов теплопроводность является важным свойством, например, для ощущения холода / тепла для волокон одежды или деревянных изделий, или при теплоизоляции пластмасс, включая стирофоры [1– 4]. С недавним развитием технологий сверхпроводимости и электронной техники, теплопроводность конструкционных и изоляционных материалов, используемых в качестве композитов в криогенных и тепловыделяющих материалах в электрическом оборудовании, стала более важной.Кроме того, желаемые характеристики варьируются в зависимости от применения, от изоляции для использования в криостате [5] до высокой теплопроводности для использования в сверхпроводящих катушках [6] и электронной технике [7]. Например, теплопроводность между сверхпроводником и холодной головкой холодильника важна для стабильности сверхпроводящей катушки с кондуктивным охлаждением, поскольку это соединение является единственным каналом теплового потока для охлаждения сверхпроводника [8].
Теплопроводность большинства полимерных материалов ниже, чем у металлов, как показано на Рисунке 1.Из предыдущих исследований полимерных материалов хорошо известно, что теплопроводность аморфных полимеров меньше, чем у металлов и полупроводников [9, 10]. Поэтому они в основном использовались в качестве теплоизоляторов. Однако в других сообщениях показано, что полимерные кристаллы обладают высокой теплопроводностью в том направлении, в котором молекулярные цепи ковалентно связаны, например, кристаллы полиэтилена [11, 12]. Таким образом, высококристаллизованные и высокоориентированные полимеры обладают высокой теплопроводностью [10–15].Например, высококристаллизованные полимерные материалы, включая высокопрочное полиэтиленовое (PE) волокно [15–18] и высокопрочное полипара-фенилен-бензобис-оксазол (PBO) волокно [16], как известно, обладают высокой теплопроводностью, аналогичной те из металлов, как показано на рисунке 2. Высокопрочные волокна PE и волокна PBO, показанные на рисунке 2, представляют собой Dyneema® SK-60 (далее сокращенно DF) и Zylon® HM (TOYOBO CO.) [18–20].

В этой статье мы сообщаем о теплопроводности высокопрочного полиэтиленового волокна и применении высокопрочного пластика, армированного полиэтиленовым волокном, для высокотемпературной сверхпроводящей катушки с кондуктивным охлаждением.
2. Теплопроводность высокопрочного полиэтиленового волокна
2.1. Теплопроводность полимерного волокна
Теплопроводность твердых электроизоляционных материалов вводится за счет фононов [12, 13], а тепло в полимерах проводится в направлении ковалентно связанных молекулярных цепей, тогда как теплопроводность в направлении к межмолекулярным цепям. цепей, скрепленных силами Ван-дер-Ваальса, намного меньше. Известно, что теплопроводность ПЭ, полиэтилентерефталата и полипропилена в направлении молекулярной цепи увеличивается за счет увеличения кристалличности и ориентации кристалла [11, 13–17, 21, 22].В случае аморфных полимеров также известно, что теплопроводность полиметилметакрилата и полистирола увеличивается за счет ориентации молекулярной цепи [16, 23, 24].
На теплопроводность твердых электроизоляционных материалов влияет рассеяние фононов. Считается, что рассеяние фононов связано с дефектами материала. Например, кристаллическая или аморфная граница, дефекты, точки химических мостиков, а также концы и перепутывания молекулярных цепей могут рассеивать фононы и влиять на коэффициент теплопередачи в полимерных материалах.О зависимости теплопроводности от молекулярной массы сообщалось о пленке из полистирола [25].
В случае полимерных волокон теплопроводность в направлении волокон зависит от кристалличности, ориентации, размера кристаллов, длины молекулярных цепей, точек химических мостиков и морфологии, состоящей из кристаллов и аморфных.
Например, теплопроводность волокна рами в направлении волокна изменяется при следующих обработках, втягивании воды (водоподготовка), облучении γ -лучами (обработка γ -лучами) и парофазной обработкой формальдегидом. (Лечение VP-HCHO).Эти обработки вызывают удлинение, разрыв цепи и образование мостиков в молекулярных цепях, как показано на Рисунке 3 [26–28]. Теплопроводность волокон рами до и после этих обработок показана на Рисунке 4 [26–28].

Сообщается, что модуль упругости увеличивается за счет увеличения степени ориентации молекулярных цепей в аморфной области волокна рами за счет обработки водой [31]. Также известно, что модуль упругости волокна рами увеличивается при обработке воды [31].Теплопроводность волокна рами в направлении волокон увеличивается при обработке водой, как показано на рисунке 4 [26]. При такой водной обработке волокна рами вытягивались под действием напряжения 17,4 кг / мм ² в воде. Модуль упругости волокна рами при такой водной обработке удваивается. Предполагается, что увеличение теплопроводности в результате обработки воды вызвано удлинением молекулярных цепей в аморфной области, как показано на рисунке 3 [26].
Хорошо известно, что волокна, в основном состоящие из целлюлозы, включая рами и хлопок, подвергаются разрыву основной цепи обработкой γ -лучами [32], как показано на рисунке 3.Также известно, что кристалличность не снижается при облучении γ -лучами при соответствующей мощности дозы [27, 32]. Теплопроводность волокна рами в направлении волокна уменьшается при обработке γ -лучами, как показано на рисунке 4 [27]. Сообщается, что снижение теплопроводности волокна рами при обработке γ -лучами согласуется с уменьшением степени полимеризации (DP) волокон рами. В этом случае, показанном на рисунке 4, облучение проводилось γ -лучами Co-60, а общая поглощенная доза составляла 100 кГр [27].DP волокон рами снижается с 1700 до 220 при такой обработке γ -лучами. Предполагается, что уменьшение теплопроводности при обработке γ -лучами вызвано разрывом молекулярной цепи. То есть теплопроводность волокон рами зависит от длины молекулярной цепи [27].
Волокна, в основном состоящие из целлюлозы, включая рами и хлопок, хорошо известны тем, что они связаны с формальдегидом (HCHO) [31, 37, 39–44], например, обработкой VP-HCHO [39], как показано на рисунке 3 .Эта технология используется для стабилизации соответствия целлюлозных волокон и используется практически в материалах одежды, таких как стирка и рубашки [40, 42–45]. Теплопроводность снижается примерно до 20–25% при обработке VP-HCHO, как показано на Рисунке 4 [28]. Сообщается, что теплопроводность уменьшается при увеличении концентрации связанного HCHO [28]. В этом случае, как показано на рисунке 4, концентрация связанного HCHO в волокне рами, обработанном VP-HCHO, составляла 1,6% [28]. Предполагается, что уменьшение теплопроводности волокна рами при обработке VP-HCHO вызвано рассеянием фононов в точках перемычки в сочетании с HCHO [28].
Таким образом, теплопроводность волокон рами увеличивается за счет увеличения ориентации молекулярных цепей и уменьшается за счет разрыва цепей или мостиков в молекулярных цепочках [26–28]. То есть теплопроводность полимерных волокон зависит от структур, например, ориентации, длины (молекулярной массы) и точек перемычки молекулярных цепей.
2.2. Теплопроводность высокопрочного полиэтиленового волокна
2.2.1. Полимерное волокно с высокой теплопроводностью
Как упоминалось выше, высокопрочное полиэтиленовое волокно имеет высокую теплопроводность в направлении волокон [18–20].DF, показанный на рисунке 2, является одним из высокопрочных волокон PE сверхвысокой молекулярной массы (UHMW), полученных методом гелевого прядения [46–51]. В этом разделе описывается механизм высокой теплопроводности DF.
Хорошо известно, что хаотически ориентированная кристаллическая область, состоящая из сворачивающихся цепочек СВМПЭ, изменяется на высокоориентированную кристаллическую область, состоящую из протяженных цепочек, путем вращения геля, как показано на Рисунке 5 [29, 46–51]. Поэтому считается, что теплопроводность вытянутых цепей в направлении оси ковалентно связанных цепей в кристаллических областях способствует высокой теплопроводности ДФ [18–20].

Взаимосвязь между теплопроводностью и структурой DF описана ниже.
2.2.2. Зависимость теплопроводности от модуля упругости высокопрочного полиэтиленового волокна [20]
Теплопроводность высокопрочных волокон из сверхвысокомолекулярного полиэтилена (далее сокращенно ПЭФ), изготовленных методом формования геля с различными степенями вытяжки, показана на рисунке 6 [20] . Они имеют разные модули упругости, показанные ниже: A: 15 ГПа, B: 51 ГПа, C (DF): 85 ГПа и D: 134 ГПа.Теплопроводность увеличивается с увеличением модуля упругости PEF, и все они увеличиваются с увеличением температуры, как показано на рисунке 6. Соотношения между теплопроводностью и модулем упругости PEF показаны на рисунке 7. Теплопроводность PEF увеличивается линейно пропорционально модуль упругости при растяжении.

Взаимосвязь между теплопроводностью и модулем упругости PEF была объяснена структурой волокна, проиллюстрированной в механической последовательно-параллельной модели (модель Такаянаги), которая состоит из кристаллической / аморфной структуры, как показано на рисунке 8 [ 20].Эта механическая модель состоит из следующих двух частей путем параллельной комбинации. Одна из них представляет собой непрерывную кристаллическую часть, состоящую из протяженных молекулярных цепочек, а другая – последовательную комбинацию кристаллической и аморфной частей. В этой механической модели, состоящей из непрерывной кристаллической области и последовательной комбинированной части, состоящей из кристалла и аморфного вещества, теплопроводность PEF в направлении волокна преобладает над теплопроводностью непрерывной кристаллической области, состоящей из протяженных молекулярных цепочек [20].

2.2.3. Влияние излучения на теплопроводность высокопрочного полиэтиленового волокна с помощью
γ -луча [30]
В этом разделе сообщается о вкладе в теплопроводность длины молекулярных цепей в высокопрочном полиэтиленовом волокне. Известно, что полиэтилен подвергается разрыву основной цепи при облучении γ -лучами (обработка γ -лучами) в присутствии кислорода [52].
Значения теплопроводности PEF с обработкой γ -лучами показаны на рисунке 9 [30].Используемый PEF был DF. Облучение проводили лучами Co-60 γ , общая поглощенная доза составляла 0,5 МГр; который здесь и далее сокращенно обозначается DF (обработка γ -лучами). DF без обработки γ -лучами сокращенно обозначается DF (пустой). Теплопроводность DF снижается до 50% при обработке γ -лучами при каждой температуре [30].

Измеренная молекулярная масса DF (бланк) составляла 2,0 × 10 ⁶. Он уменьшился до 2,6 × 10 ⁴ на 0.Облучение 5 МГр. Этот результат показывает расщепление основной цепи DF обработкой γ -лучами. С другой стороны, изменение кристаллической структуры DF при обработке γ -лучами не наблюдалось. Таким образом, уменьшение теплопроводности DF при обработке γ -лучами было объяснено разрывом основной молекулярной цепи как аналогично случаю рами, описанному выше. Этот результат предполагает влияние длины протяженных молекулярных цепей из-за высокой молекулярной массы на теплопроводность DF [30].
2.2.4. Резюме
С вышеупомянутым высокопрочное полиэтиленовое волокно имеет высокую теплопроводность в направлении волокон, и эта высокая теплопроводность объясняется механической последовательно-параллельной моделью, состоящей из кристаллов и аморфных, включая непрерывную кристаллическую область, состоящую из длинных протяженных молекулярных цепочек [ 20, 30].
2.3. Теплопроводность высокопрочных пластиков, армированных полиэтиленовым волокном [18, 53]
Для того, чтобы применять PEF в криогенных целях, например, в катушках катушек или прокладке сверхпроводящих катушек, важна теплопроводность пластиков, армированных PEF, как описано в следующих разделах.В этом разделе PEF, используемый в качестве арматуры, – это DF. В дальнейшем пластики, армированные DF, сокращенно DFRP. Принципиальная схема однонаправленного (UD) DFRP показана на рисунке 10.

Теплопроводность UD-DFRP параллельно и перпендикулярно направлению волокна показана на рисунке 11 [18]. Теплопроводность DFRP параллельно направлению волокон имеет примерно среднее значение между DF и эпоксидной смолой. Зависимость теплопроводности от объемной доли (Vf) DF в UD-DFRP показана на рисунке 12.Теплопроводность UD-DFRP пропорциональна Vf DF, как показано на Рисунке 12 [18]. Следовательно, теплопроводность DFRP параллельно направлению волокна пропорциональна коэффициенту поперечного сечения DF, ориентированного в направлении проводимости [18].

Теплопроводность UD-DFRP в перпендикулярном направлении волокна на порядок меньше, чем в направлении, параллельном волокну [18].
Известно, что теплопроводность гибридного стеклопластика, включающего ДФ, может быть выражена законом смесей [53].
3. Применение высокопрочных пластиков, армированных полиэтиленовым волокном, для высокотемпературной сверхпроводящей катушки с кондуктивным охлаждением
3.1. Нестабильность ВТСП-катушки из-за локального повышения температуры ВТСП-ленты
Когда охлаждающая способность холодильника превышает потери в ВТСП-катушке и теплопроводность по токопроводам, возможна стационарная работа катушки с кондуктивным охлаждением [54]. Однако, если условия охлаждения ВТСП ленты в катушке частично недостаточны, локальное горячее пятно возникает в катушке с кондуктивным охлаждением во время работы катушки [55].Локальное повышение температуры ленты является одной из нестабильностей ВТСП-катушек с кондуктивным охлаждением. Чтобы предотвратить локальное повышение температуры ВТСП-ленты, необходимо эффективно отводить тепло от ВТСП-ленты к электроизоляционным материалам в катушке. Для эффективного отвода тепла от ВТСП-ленты к электроизоляционным материалам необходим электроизолятор с высокой теплопроводностью для катушки или проставки [6].
Обычно в качестве электроизоляционных материалов для ВТСП катушки использовались армированные стекловолокном (GF-) пластмассы (GFRP), например, катушка катушки или распорка.Однако стеклопластик – это теплоизолятор. Следовательно, отвод тепла от ленты HTS к GFRP недостаточен. С другой стороны, нитрид алюминия (AlN) известен как электрический изолятор и теплопроводник. Однако AlN твердый и хрупкий, поэтому изготовителям катушек и пользователям трудно обрабатывать детали электрической изоляции в катушке, например, прокладки [6].
В следующих разделах описывается эффект отвода тепла из пластиков, армированных PEF, на электроизоляционный материал катушек HTS.Армированный DFRP пластик используется как PEF-армированный пластик в следующих разделах.
3.2. Важные физические свойства высокопрочных пластиков, армированных полиэтиленовым волокном, для катушек HTS
В этом разделе сообщается о важных физических свойствах DFRP, за исключением теплопроводности, для того чтобы описать катушки HTS в следующих разделах. Коэффициенты трения, поверхностные искровые напряжения и тепловое сжатие при охлаждении DFRP показаны на рисунках 13, 14 и 15.DFRP имеет более низкий коэффициент трения и более высокое напряжение искры, чем GFRP [33, 34]. DFRP имеет отрицательный коэффициент теплового расширения в направлении волокна [35, 36]. Следовательно, DFRP расширяется в направлении волокна за счет охлаждения от комнатной температуры до температуры жидкого азота, как показано на Рисунке 15 [35, 36].

3.3. Эффект отвода тепла от ВТСП-лент к высокопрочным пластмассам, армированным полиэтиленовым волокном [38]
В этом разделе описывается эффект отвода тепла от ВТСП-лент с установившимся током на ВТСП-ленту.Схематическая иллюстрация экспериментальной установки показана на рисунке 16. Bi-2223 используется в качестве HTS-ленты в этом разделе. DFRP, GFRP и AlN использовались в качестве конструкционных материалов на фиг. 16. Объемная доля волокна из DFRP и GFRP составляла 50% (далее сокращенно DFRP-50 и GFRP-50). В качестве зажимных материалов использовались конструкционные материалы. Характеристики зажимных материалов и ленты Bi приведены в таблице 1. Набор зажимных материалов, зажимная лента и груз указаны на холодной головке холодильника и охлаждают до 77 К.К ленте подавался постоянный ток 60 А, равный критическому току ленты Bi, и наблюдалось напряжение между лентами [38].
Лента Bi2223 Зажимные материалы
Ширина (мм) 4,1 9
30 918 Толщина (мм) 9
Длина (мм) 150 124
Коэффициент Ag 2.2
Ic при 77 K 60 A
Материал Ag, Bi-2223 DFRP, GFRP, AlN
9172 9172 9172 ленты, зажатой GFRP-50, DFRP-50 и AIN, показаны на рисунке 17. Как показано на рисунке 18, когда зажимным материалом является AlN, напряжение остается относительно низким, то есть повышение температуры лента очень медленная [38].Напротив, напряжение на GFRP-50 снижалось в течение короткого времени с момента начала тока, а повышение температуры ленты было быстрым [38]. DFRP-50 показывает среднее поведение между GFRP-50 и AlN. Повышение напряжения вызвано повышением температуры, вызванным джоулевым нагревом. Теплопроводность DFRP-50 выше, чем у GFRP-50, и ниже, чем у AlN. Следовательно, различие данных в GFRP-50, DFRP-50 и AlN связано с теплопроводностью зажимных материалов и передачей тепла от ленты Bi зажимным материалам [38].Известно, что рост напряжения замедляется при увеличении отношения содержания DF и контактного напряжения к ленте Bi в случае DFRP [38]. Считается, что отрицательное тепловое расширение DFRP способствует увеличению контактного напряжения в HTS-катушке. О стабильности катушки HTS сообщается в следующем разделе.

3.4. Оценка эффективности охлаждения высокопрочных пластиков, армированных полиэтиленовым волокном, в ВТСП-змеевиках с кондуктивным охлаждением [8]
В этом разделе сообщается о термической стабильности ВТСП-катушек, состоящих из катушек из DFRP, GFRP и AlN, показанных на рисунке 18.Бобины из DFRP и GFRP представляли собой трубы, показанные на Рисунке 19, и они были изготовлены методом намотки нитей (FW). Образцы катушки и сверхпроводника показаны в таблице 2. Углы FW труб из DFRP составляли 30, 45 и 60 градусов. Они обозначаются как DFRP60, DFRP30 и DFRP45 соответственно. Если угол больше 45 градусов, шпулька расширяется в радиальном направлении при охлаждении [36]. С другой стороны, когда она меньше 45 градусов, шпулька сжимается при охлаждении [36]. Угол FW GFRP составлял 60 °. Бобины из AlN и GFRP не расширяются при охлаждении.
Катушка и шпулька Высота (мм) 50
Внутренний диаметр шпульки (мм) 40
Наружный диаметр шпульки (мм) 55
Поворот / слой 4 витка и однослойный
Натяжение обмотки 10 Н при комнатной температуре
Проводник Сверхпроводник Bi-2223
Оболочка Серебряный сплав
Ширина (мм) 3.3
Толщина (мм) 0,7
Соотношение серебра 2,2
Ic при 77 K 86A

Профили времени Сигналы ленты напряжения этих катушек показаны на рисунке 20. Ток, приложенный к ВТСП-катушке, соответствует 86 А (Ic). Профиль напряжения катушки AlN почти такой же, как у катушки DFRP60, даже несмотря на то, что теплопроводность AlN более чем в два раза больше, чем у DFRP60 [56].Причина в передаче тепла от ленты к шпульке. Бобина из DFRP60 расширилась, и, следовательно, ее теплоотдача стала лучше [57]. Бобина из AlN сжималась, и ее теплоотдача ухудшалась. Теплопроводность GFRP ниже, чем у других четырех материалов, использованных в эксперименте, а теплопередача змеевика GFRP плохая, потому что материал сжимается при охлаждении. Вот почему измеренная термическая стабильность была худшей для катушки, намотанной на бобину из стеклопластика.Следовательно, термостойкость катушек зависит не только от теплопроводности бобины, но и от передачи тепла от ленты к бобине. Таким образом, DFRP60 может быть хорошим теплоотводом для бобины катушки с кондуктивным охлаждением [8].

Теплопроводность с коэффициентом теплопроводности, зависящим от температуры
1.
К. Ф. Бонилла, Ядерная инженерия, МакГроу-Хилл, Нью-Йорк (1957).
Google ученый
2.
Х. С. Карслав и Дж. К. Джегер, Проводимость тепла в твердых телах, 2-е изд., Oxford University Press, Оксфорд (1959).
Google ученый
3.
Дж. Крэнк, Математика диффузии, Издательство Оксфордского университета, Оксфорд (1956).
Google ученый
4.
J. Pfann, Nucl. Англ. Дизайн, 4 , 121 (1966).
Google ученый
5.
М. А. Био, Дж. Аэрон. Sci., 24, , 857 (1957).
Google ученый
6.
M. A. Biot, J. Aerospace Sci., 26 , 367 (1959).
Google ученый
7.
Ф. Дж. Ларднер, AIAAJ., 1, 196 (1963).
Google ученый
8.
D. F. Hays, Int. J. Теплопередача, 9 , 165 (1966).
Google ученый
9.
Д. Ф. Хейс, Вариационная формулировка уравнения теплопроводности: температурно-зависимая теплопроводность, стр. 17, в: Неравновесная термодинамика, вариационные методы и стабильность, Р. Дж. Донелли, Р. Херманн и И. Пригожин (редакторы) , Издательство Чикагского университета, Чикаго (1966).
Google ученый
10.
Э. Л. Даути, Таблицы решений для переходной теплопроводности в материалах с переменной теплопроводностью.An. Встретиться. Чикаго 111, ноябрь 1965 г., ASME.
11.
Х. С. Шехтер, Вариационный метод в инженерии, Макгроу-Хилл, Нью-Йорк (1967).
Google ученый
12.
Михлин С. Г. Вариационные методы в математической физике, Pergamon Press (1964).
13.
Ф. Б. Хильдебрауд, Методы прикладной математики, 2-е изд. Prentice-Hall Inc. (1965).
Теплопроводность платиновых сплавов при высоких температурах
Преимущество использования платины (Pt) в промышленных целях обусловлено ее уникальными свойствами, такими как каталитическая активность, высокая температура плавления (1), пластичность (2, 3) химическая инертность в широком диапазоне температур (4, 5).Платина использовалась для биомедицинских компонентов, специальных химикатов, топливных элементов и катализаторов контроля загрязнения, таких как автомобильные выхлопы, а также для ювелирных изделий, термопар и катодной защиты корпусов судов (3).
Одно из типичных применений платины – электронные устройства, причем толстопленочные проводники являются одними из основных продуктов (6). Легирующие элементы, выбранные из металлов платиновой группы и благородных металлов, обычно используются для повышения прочности или защиты поверхности от неблагоприятных условий эксплуатации (3).Однако добавление легирующего элемента может ухудшить проводимость. До сих пор данные о проводящих свойствах платиновых сплавов были ограничены (7-12).
Настоящее исследование посвящено изучению параметров теплопроводности различных платиновых сплавов при высоких температурах. Сначала будет исследована зависимость теплопроводности от состава, и результаты будут упорядочены в соответствии с Периодической таблицей; во-вторых, будет исследован эффект наклепа; и в-третьих, будет исследована температурная зависимость теплопроводности.
Зависимость теплопроводности от состава
Зависимость теплопроводности сплавов Pt от концентрации растворенного вещества при 300 K показана на рисунке 1 вместе с данными для чистой Pt (1, 13, 14). Ванадий (V) и никель (Ni) были выбраны в качестве растворенных веществ. Никель принадлежит к тому же столбцу, что и Pt в Периодической таблице (Pt-Ni – изоэлектронная система), в то время как V расположен горизонтально на большом расстоянии от Pt (Pt-V – неизоэлектронная система). Все сплавы, использованные в этом исследовании, имеют гранецентрированную кубическую форму (f.c.c.) однофазный; тогда как в системе Pt-V преобразование порядок-беспорядок происходит при стехиометрии 3: 1. Данные для Pt ₃ V с ГЦК. неупорядоченная структура и упорядоченная структура D0 ₂₂ взяты из более ранней работы (15). Обратите внимание, что термообработка при 1573 К в течение 1 часа была предпринята для достижения неупорядоченного состояния в Pt ₃ V, в то время как старение при 1020 К в течение 168 часов использовалось для реакции упорядочения.
Рис. 1
Зависимость теплопроводности от состава при 300 K в сплавах Pt-Ni и Pt-V.Данные для чистой Pt представлены сплошным квадратом на оси (1, 13, 14). Рекомендуемые значения для чистой Pt в этих источниках данных аналогичны. Сплошной треугольник – данные для Pt ₃ V с упорядоченной структурой D0 ₂₂ (15)
Теплопроводность чистой Pt, обнаруженная в настоящем эксперименте, составила 77,8 Вт · м ^-1 K ^-1 , что несколько выше литературных значений (1, 13, 14). Оно монотонно уменьшалось с увеличением концентрации растворенного вещества для обоих сплавов.В используемых диапазонах составов графики проводимость-состав в каждом случае характеризуются резким максимумом для чистой Pt. Зависимость от состава более выражена в сплаве Pt-V, при добавлении всего двух атомных процентов V теплопроводность Pt снижается наполовину. Скорость снижения теплопроводности становится меньше при более высоких концентрациях V, обычно выше десяти атомных процентов.
Из рисунка 1 видно, что теплопроводность увеличивается при образовании упорядоченной фазы D0 ₂₂ в составе Pt ₃ В.Это увеличение проводимости за счет упорядочения, по-видимому, является общей чертой, которая также демонстрируется для Pt ₃ Cr со структурой L1 ₂ и для Ni ₃ V (D0 ₂₂), Ni ₃ Mn ( L1 ₂) и Ni ₃ Fe (L1 ₂) (15). Теплопроводность обычно ухудшается из-за рассеяния носителей заряда в кристаллической решетке. Топологический и конфигурационный беспорядок, такой как примеси, вакансии и дефекты решетки, препятствуют потоку теплоносителей.Следовательно, хорошо упорядоченные интерметаллические соединения должны иметь более высокую проводимость, чем их неупорядоченные сплавы, при условии, что концентрации носителей не изменяются в обеих фазах (16).
Главный вопрос, на который необходимо ответить, – это то, что отвечает за теплопроводность в сплавах Pt. Теплопроводность металлических материалов обычно складывается из электронного и фононного компонентов. Соотношение Видемана-Франца является критерием идентификации носителя теплопроводности.Закон Видемана-Франца гласит, что при высоких температурах отношение теплопроводности к электрической проводимости (обратное удельному сопротивлению) для всех металлов пропорционально абсолютной температуре. Когда электронный компонент вносит основной вклад в общую теплопроводность λ, соотношение Видемана-Франца должно выполняться (17-19), как в (Уравнение i):
(i)
, где L – число Лоренца, T – абсолютная температура, а σ – электропроводность.Константа универсальности λ / σ оказалась равной 7,5 · 10 ^-6 Ом · К ^-1 при 300 К для чистых металлов (17).
Соотношение Видеманна-Франца было исследовано для исследуемых здесь сплавов Pt. На рис. 2 показан график зависимости электропроводности (обратной величины удельного электрического сопротивления) от теплопроводности для сплавов Pt-Ni и Pt-V. Прямая линия указывает соотношение Видемана-Франца, заданное (Уравнение i) при 300 К. Все графики для сплавов Pt, включая чистую Pt, близки к этой линии.Это указывает на то, что сплавы Pt удовлетворяют соотношению Видемана-Франца при 300 К, даже высококонцентрированные сплавы.
Таким образом, доминирующий носитель теплопроводности в сплавах Pt приписывается электрону, а не фонону: более конкретно, 6 s электронов считаются ответственными за теплопроводность.
Рис. 2
Соотношение Видемана-Франца для сплавов Pt-Ni и Pt-V при 300 К. Составы сплавов в атомных процентах
Зависимость от компонентов
Рисунок 1, зависимость теплопроводности от состава в сплавах Pt показывает, что имеет место резкое снижение теплопроводности при низких концентрациях растворенного вещества, до 2 атомных процентов, по сравнению со значением для чистой Pt.Хорошо известно, что Pt имеет широкий диапазон растворимости в твердом состоянии для большинства легирующих элементов (20). В этом разделе мы сосредоточимся на теплопроводности различных сплавов Pt-2 ат.% X, чтобы определить влияние растворенного вещества X на теплопроводность Pt.
На рисунке 3 приведены значения теплопроводности сплавов Pt-2 ат.% X при 300 К. Растворенное вещество X расположено в порядке периодической таблицы. Можно ясно видеть, что добавление растворенного элемента снижает теплопроводность Pt. Когда растворенное вещество X принадлежит к B-подгруппе (Cu, Ga, Ge) в первый длительный период, теплопроводность монотонно уменьшается по мере увеличения горизонтального расстояния X от растворителя Pt.Эта тенденция также сохраняется для растворенного вещества X во втором длительном периоде. Стоит отметить, что Al и Si, расположенные над Ga и Ge соответственно, также попадают на одну линию.
Рис. 3
Зависимость теплопроводности сплавов Pt-2 ат.% X от атомного номера растворенного вещества X при 300 K.
Сплошной черный квадрат показывает теплопроводность чистой Pt.
Данные для Pt-2 ат.% Al и Pt-2 ат.% Si представляют собой сплошные ромбовидные символы.
As, Pb и Bi не растворяются в Pt (20).
Данных по Tc нет, поскольку сплав нестабилен.
Нет данных для Zn, Cd, Hg и Tl, так как их более низкие температуры кипения препятствуют получению слитков сплава дуговой плавкой
Эта тенденция наблюдалась для удельного электрического сопротивления и известна как правило Норбери (21). Норбери изучал изменение удельного электросопротивления при добавлении растворенных веществ к Fe, Ni, Cu, Ag, Au и Mg, а также к расплавленным состояниям Na и K. Эмпирическим правилом было обнаружено, что удельное электрическое сопротивление бинарных сплавов увеличивается по мере того, как положение в Периодическая таблица растворенного элемента становится горизонтально удаленной от таковой основного компонента.Текущие результаты подразумевают, что правило Норбери в целом справедливо для явлений переноса, вызванных электронами. В отличие от случая элементов B-подгруппы, однако, поведение более сложное, когда растворенное вещество принадлежит остальным переходным элементам. В течение первого длительного периода теплопроводность монотонно уменьшается с увеличением расстояния X от Pt. Это ломается на Mn. Разрушение происходит на элементах, удаленных от Pt, когда растворенное вещество X принадлежит третьему длинному периоду. Примечательно, что Re наиболее существенно снижает теплопроводность Pt.Также заслуживает внимания тот факт, что значения теплопроводности очень похожи друг на друга для растворенных веществ, принадлежащих к одной и той же колонке, что обычно демонстрируется в колонках IVA, VA и VIII (Fe, Ru, Os). Данные на рисунке 3 также предполагают, что теплопроводность больше зависит от столбца растворенного вещества X и меньше зависит от периода.
Зависимость от деформационного упрочнения
Для изучения чувствительности к условиям изготовления была исследована теплопроводность как функция обжатия при холодной прокатке для некоторых сплавов Pt.На рис. 4 показаны результаты для чистой Pt и трех сплавов Pt. Небольшое снижение теплопроводности наблюдалось в чистой Pt, обычно при обжатии при холодной прокатке более 30%, в то время как довольно постоянное значение сохраняется для высококонцентрированных сплавов с более низкой проводимостью. Результаты показывают, что теплопроводность этих сплавов в основном определяется исходным составом, а не дефектной структурой, возникающей в процессе изготовления.
Рис. 4
Зависимость теплопроводности чистых платиновых и платиновых сплавов от обжатия при холодной прокатке.Значения теплопроводности были измерены при 300 K
Температурная зависимость
Зависимость теплопроводности сплавов Pt-Ni от температуры показана на рисунке 5 вместе со значениями для чистой Pt из источников данных, представленных пунктирной линией. (13, 14). Теплопроводность чистой Pt, измеренная в настоящем исследовании, монотонно увеличивается с повышением температуры и достигает примерно 95 Вт · м ^-1 K ^-1 при 1100 K.Монотонный рост подтверждается и для справочных данных, хотя величина систематически ниже. Добавление Ni не изменяет общую тенденцию к монотонному увеличению, а только приводит к сдвигу всех данных к более низким значениям. Более того, внимательное наблюдение показывает, что температурный коэффициент становится больше с увеличением концентрации никеля, и все данные, похоже, сходятся при более высоких температурах.
Рис. 5
Зависимость теплопроводности от температуры для сплавов Pt-Ni.Данные для чистой Pt, рекомендованные в источниках данных, показаны пунктирной линией (13, 14). Значения из источников данных аналогичны
Температурный коэффициент α в диапазоне температур от 300 до 1100 K был первоначально оценен из (Уравнение ii):
, где λ _{300 K} и λ _{1100 K} – коэффициенты теплопроводности при указанных температурах. На рисунке 6 температурные коэффициенты, полученные для сплавов Pt, представлены в зависимости от теплопроводности при 300 К.
Рис. 6
Корреляция при 300 K между теплопроводностью и температурным коэффициентом для сплавов Pt-Ni и Pt-V. Каждое значение имеет состав сплава.
Десять значений для сплавов Pt-2 ат.% X нанесены на график.
Элементы X из второго длительного периода
Чистая Pt имела теплопроводность 77,8 Вт · м ^-1 K ^-1 при 300 K с положительным температурным коэффициентом 2,9 × 10 ^-4 К ^-1.Теплопроводность монотонно уменьшается с увеличением концентрации Ni, что сопровождается увеличением коэффициента. Такая обратная корреляция более четко видна на полулогарифмическом графике, см. Рисунок 6. Интересно, что большинство сплавов Pt-V имеют такую же корреляцию, за исключением сплава Pt-16V. Более того, различные выбранные элементы из второго длительного периода, показанного светлыми квадратами, также сохраняют ту же корреляцию, что означает, что корреляция может иметь универсальную особенность. Обратная корреляция между α и λ _{300 K} может быть общей чертой для металлических материалов и была хорошо задокументирована не только для бинарных твердых растворов, но и для многокомпонентных материалов, таких как стали и суперсплавы, а также для интерметаллических соединений (15, 22).
Выводы
Теплопроводность в сплавах Pt была всесторонне исследована в зависимости от концентрации растворенного вещества, наклепа и температуры. Результаты следующие:
Теплопроводность платиновых сплавов в основном определяется как составом сплава, так и температурой и практически не зависит от деформационного упрочнения.

Материал	Температура	Теплопроводность	Температура	Теплопроводность
Адмиралтейство Латунь	20	96.1	68	55,5
	100	103,55	212	59,8
	238	116,44	460	67,3
Алюминий	20	225	68	130
	100	218	212	126
	371	192	700	111
Сурьма	20	18. 3	68	10,6
Сурьма	100	16,8	212	9,69
Бериллий	20	139	68	80,1
	100		212	76,2
	371	109	700	63,0
Латунь	-165	106	-265	61,0
	20	144	68	83.0
	182	177	360	102
Бронза	20	189	68	109
Cadmiuim	20	92,8	68	53,6
Cadmiuim	100	90,3	212	52,2
Медь	20	401	68	232
	100	377	212	218
	371	367	700	212
Золото	20	317	68	183
Германий	20	58. 8	68	34,0
Инконель X	-3	13,2	27	7,62
	20	13,7	68	7,90
	577	25,5	1070	14,7
Железо	20	71,9	68	41,6
	100	65,7	212	38,0
	371	44.6	700	25,8
Чугун (кованый)	20	60,4	68	34,9
Чугун (кованый)	100	59,9	212	34,6
Чугун (литье)	53	48,0	127	27,7
Свинец	0	35,1	32	20,3
	20	34,8	68	20.1
	260	30,3	500	17,5
Магний	20	170	68	98,5
	100	167	212	96,3
	188	163	370	93,9
Молибден	0	137	32	79,0
	20	136	68	78. 4
	427	115	800	66,7
Монель	-250	20,73	-418	11,98
	20	27,5	68	15,86
	800	46,9	1472	27,1
Никель	20	62,4	68	36,0
	100	58.0	212	33,5
	293	47,5	560	27,4
Палладий	20	67,5	68	39,0
Платина	20	71,0 900	68	41,0
	100	70,6	212	40,8
	427	69,2	800	40,0
Плутоний	20	8.65	68	5,00
Родий	20	152	68	88,0
Серебро	20	419	68	242
	100	405	212	234
	316	366	600	211
Сталь, 1% углерода	20	45,3	68	26. 2
Сталь, 1% углерода	100	44,8	212	25,9
SS ANSI 301, 302, 303, 304	35	14,0	95	8,08
	100	15,0	212	8,69
	900	28,0	1652	16,2
SS ANSI 310	0	11,9	32	6,85
	20	12.3	68	7,11
	900	32,0	1652	18,5
SS ANSI 314	30	17,3	86	10,0
	100	17,6	212	10,2
	300	18,4	572	10,6
	900	22,6	1652	13,1
SS ANSI 316	-50	13.0	-58	7,51
	20	13,9	68	8,04
	950	26,1	1742	15,1
SS ANSI 321, 347, 348	– 70	14,3	-94	8,25
	20	15,7	68	9,06
	900	29,4	1652	17,0
SS ANSI 403, 410, 416 , 420	-70	26. 0	-94	15,0
	20	26,0	68	15,0
	1000	26,0	1832	15,0
SS ANSI 430	50	21,8	122	12,6
SS ANSI 430	900	25,0	1652	14,4
SS ANSI 440	100	22,1	212	12.8
SS ANSI 440	500	27,5	932	15,9
SS ANSI 446	0	22,4	32	13,0
	20	22,7	68	13,1
	1000	38,0	1832	22,0
SS ANSI 501, 502	30	37,0	86	21,4
	100	36.2	212	20,9
	830	27,8	1526	16,0
Тантал	20	55,0	68	31,8
Таллий	0	50	32	29,0
Торий	20	29,4	68	17,0
	100	30,5	212	17.6
	299	33,3	570	19,3
Олово	20	62,1	68	35,9
Олово	100	58,8	212	33,9
Титан	20	15,6	68	9,00
	100	15,3	212	8,86
	299	14.7	570	8,50
Вольфрам	20	159	68	92,0
	100	154	212	89,2
	299	142	570	82,0
Уран	20	24,2	68	14,0
	100	26,0	212	15,0
	770	40.6	1418	23,4
Ванадий	20	34,6	68	20,0
Цинк	20	112	68	64,9
Цинк	100	111	212	63,9
Цирконий	0	19,0	32	11,0

Коэффициент теплопроводности это: Коэффициент теплопроводности – это… Что такое Коэффициент теплопроводности?

Коэффициент теплопроводности – это… Что такое Коэффициент теплопроводности?

Коэффициенты теплопроводности различных веществ

Коэффициент теплопроводности вакуума

Связь с электропроводностью

Обобщения закона Фурье

Примечания

См. также

Коэффициент теплопроводности, формула и примеры

Определение и формула коэффициента теплопроводности

Коэффициент теплопроводности газа

Коэффициент теплопроводности металлов

Коэффициент теплопроводности и уравнение Фурье

Единицы измерения

Примеры решения задач

Расчет коэффициента теплоотдачи на плоских и гофрированных поверхностях

Что такое коэффициент теплоотдачи?

Расчет коэффициента теплоотдачи в COMSOL Multiphysics®

Пример 1. Теплообмен при вынужденном обтекании плоской горизонтальной пластины

Моделирование сопряженного теплообмена

Расчет коэффициента теплоотдачи по формулам для числа Нуссельта

Расчет коэффициента теплоотдачи

Пример 2. Течение у гофрированной поверхности горизонтальной пластины

Заключение

Дальнейшие шаги

Список литературы

Закон Фурье. Коэффициент теплопроводности

Содержание:

Закон Фурье. Коэффициент теплопроводности

Коэффициенты теплопроводности для различных материалов

Коэффициенты теплопроводности, теплообмена и теплопередачи

Не удается найти страницу | Autodesk Knowledge Network

Теплопроводность металлов и сплавов

Теплопроводность высокопрочного полиэтиленового волокна и приложения для криогенного использования

1. Введение

2. Теплопроводность высокопрочного полиэтиленового волокна

2.1. Теплопроводность полимерного волокна

2.2. Теплопроводность высокопрочного полиэтиленового волокна

2.2.1. Полимерное волокно с высокой теплопроводностью

2.2.2. Зависимость теплопроводности от модуля упругости высокопрочного полиэтиленового волокна [20]

2.2.3. Влияние излучения на теплопроводность высокопрочного полиэтиленового волокна с помощью

2.2.4. Резюме

2.3. Теплопроводность высокопрочных пластиков, армированных полиэтиленовым волокном [18, 53]

3. Применение высокопрочных пластиков, армированных полиэтиленовым волокном, для высокотемпературной сверхпроводящей катушки с кондуктивным охлаждением

3.1. Нестабильность ВТСП-катушки из-за локального повышения температуры ВТСП-ленты

3.2. Важные физические свойства высокопрочных пластиков, армированных полиэтиленовым волокном, для катушек HTS

3.3. Эффект отвода тепла от ВТСП-лент к высокопрочным пластмассам, армированным полиэтиленовым волокном [38]

3.4. Оценка эффективности охлаждения высокопрочных пластиков, армированных полиэтиленовым волокном, в ВТСП-змеевиках с кондуктивным охлаждением [8]

Теплопроводность с коэффициентом теплопроводности, зависящим от температуры

Теплопроводность платиновых сплавов при высоких температурах

Зависимость теплопроводности от состава

Рис. 1

(i)

Рис. 2

Зависимость от компонентов

Рис. 3

Зависимость от деформационного упрочнения

Рис. 4

Температурная зависимость

Рис. 5

Рис. 6

Выводы

Добавить комментарий Отменить ответ