Супердиффузионная мембрана что это такое: Супердиффузионная мембрана (пленка): Что это такое

Содержание

Диффузионные и супердиффузионные мембраны для крыши

Как известно, гидроизоляционные пленки защищают конструкцию дома, крыши и утеплителя от попадания влаги и применяются как противоветровый материал, сохраняя тепло внутри помещения.

Виды диффузионных мембран для гидроизоляции мансарды

Диффузионные мембраны помимо всех характеристик обычных пленок для гидроизоляции включают в себя дополнительный слой (мембрану) с повышенной паропроницаемостью. Она позволяет парам влаги свободно выходить наружу, при этом препятствуя проникновению внешней влаги в теплоизоляцию. Это возможно благодаря наличию в паропроницаемом слое микропор размером от 1 до 2 микрон.

Выход излишнего пара со стороны утеплителя в виде конденсата

С такими свойствами диффузионные мембраны часто применяют при строительстве дома с утепленной мансардой и при утеплении фасада здания, поскольку гидроизоляционную пленку можно укладывать непосредственно на теплоизоляцию (утеплитель) без зазора.

Гидроизоляционные мембраны бывают двух, трех и даже четырехслойные. Пленки, состоящие из трех и более слоев называют супердиффузионными. Коэффициент пропускания пара данных пленок значительно выше. К тому же супердиффузионные мембраны обладают высокой плотностью, а значит будут служить значительно дольше. Как правило, плотность таких пленок выше 100 г/м2.

Укладка диффузионной пленки

Пленки укладываются цветным изображением наружу (к кровельному материалу) с нахлестом 10см (обычно на диффузионных мембранах есть специальные разметки). Для наибольшей эффективности и теплоизоляции места стыков пленок проклеиваются специальным скотчем, особенно если уклон крыши ниже 25°. Пленки повышенной плотности можно стелить без провисания, плотно натягивая мембрану на стропильные балки. Для фиксации мембраны применяют строительный степлер. Нет необходимости слишком закреплять гидроизоляцию к деревянной конструкции, поскольку в дальнейшем поверх пленки будет установлена контробрешетка.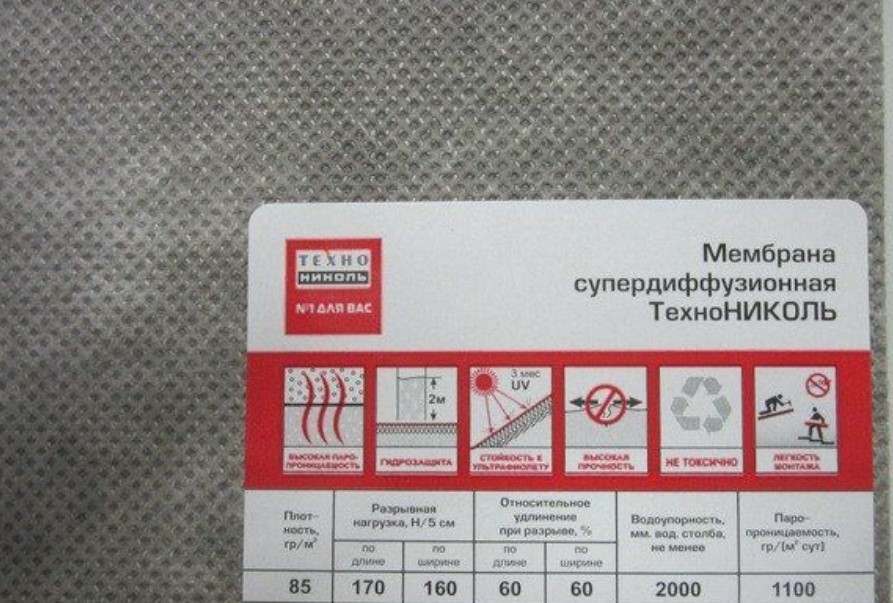

В случае примыкания гидроизоляции к стене, трубе или парапету места стыка необходимо дополнительно проклеить лентой на битумной основе или использовать специальный кровельный клей для герметизации диффузионной мембраны и конструкций из кирпича, бетона или дерева.

Супердиффузионная мембрана – dahbud site

Супердиффузионная мембрана Мастерпласт

MASTERMAX 3 TOP

Материал: паропроницаемая, трехслойная кровельная пленка (между двумя слоями полипропиленого флиза паропроницаемая, водонепроницаемая мембрана).

Сфера применения: в качестве паропроницаемой подкладочной кровельной пленки в проветриваемых кровельных конструкциях, помещается непосредственно на теплоизоляцию, является подкладочным слоем, обеспечивающим второстепенную защиту от проникающей через кровлю влажности и снега. MASTERMAX® 3 TOP применяют при строительстве с различными теплоизоляционными материалами, а также со всеми типами кровельных конструкций. Мембрана монтируется с небольшим провисанием или непосредственно на тепловую изоляцию стороной с надписью к кровле. Величина перекрытия пленок при угле наклона больше чем 30

0– 10 см, при 20-30⁰ – 15 см. Расстояние между пленкой и кровлей должно составлять не менее 3 см. Технические характеристики: 140 г/м², прочность на разрыв – продольная/поперечная-240/170 Н/50 мм, жаростойкость- +70⁰С, водонепроницаемость, Sd = 0,04 м. Стойкость к УФ-излучению: 4 недели.
Фасовка: 1,5 м*50 пм = 75 м²/рулон

MASTERMAX 3 ECO

Материал: паропроницаемая, трехслойная кровельная пленка (между двумя слоями полипропиленого флиза (на английском PP non-woven) паропроницаемая, водонепроницаемая мембрана).

MASTERMAX® 3 ECO применяют при строительстве с различными теплоизоляционными материалами, а также со всеми типами кровельных конструкций. Мембрана монтируется с небольшим провисанием или непосредственно на тепловую изоляцию стороной с надписью к кровле. Величина перекрытия пленок при угле наклона больше чем 30 0- 10 см, при 20-30 0-15 см. Расстояние между пленкой и кровлей должно составлять не менее 3 см.

Технические характеристики: 100 г/м², прочность на разрыв – продольная/поперечная-170/130 Н/50 мм, жаростойкость- +70⁰С, водонепроницаемость, Sd = 0,04 м. Стойкость к УФ-излучению: 4 недели.

Фасовка: 1,5 м*50 пм = 75 м² /рулон.

И так, вершина в деле ветро-гидрозащиты достигнута. Инженерный гений создал трёхслойную супердиффузионную мембрану. А гений украинских маркетологов «родил» название для такого уникального материала: ЕВРОБАРЬЕР (:-)).

Что же это такое? Кровельная мембрана для вентилируемых скатных кровель, как для тёплых, так и холодных помещений! Она прочная и стабильная для ультрафиолетовых лучей (до 5 месяцев). Выдерживает столб воды полметра и выпускает сквозь каждый метр квадратный поверхности 1,5 литра воды. Под такой мембраной кровля прослужит целую вечность! Монтаж трехслойной супердиффузионной мембраны производится плотно к утеплителю, без зазора. Требуемый нахлёст дистанция отмечена линией. «Цветной» стороной мембрана укладывается наружу. Крепится скобками или нержавеющими гвоздями с широкой шляпкой к стропильным ногам или обрешетке.

Эти плёнки принято называть гидробарьер. В не давнем прошлом они привели к революции в технологии укладки кровельного пирога. Дешевизна такой гидроизоляции по сравнению с устаревшими битумными материалами, ничтожно малый вес, стойкость ко всем известным видам воздействия, помогли строителям и проектантам быстро переключиться на

гидробарьер. На той же эволюционной ступени в строительстве появились более технологичные и перспективные материалы.

Это плёнки и мембраны с высокой способностью пропускать пар. Такие супердиффузионные мембраны имеют более высокую цену и применяются в тех коттеджах, где их появление приносит значительную пользу косвенно. Статистика показывает, что строительные плёнки с низкой диффузионной способностью все больше уступают место эффективным мембранам. Сегодня бытует мнение, что гидробарьер подходит для не жилых чердачных помещений, для жилых комнат на мансардном этаже лучше подходят супердиффузионные мембраны.

Скачок в развитии строительного дела произошел в результате появления плёнок с высокой паропропускной способностью. Сегодня такой материал принял форму

сепердиффузионной мембраны. Супер эффект получается благодаря низкому диффузионному сопротивлению материала. Подкровельная мембрана отводит воду с внешней поверхности и выводит пар из под внутренней стороны. Дополнительный вентиляционный зазор больше не нужен, нет необходимости поднимать гидробарьер на 2 см над теплоизоляцией. Утеплитель сохраняет тепло на наружной поверхности. Оцени эффект: вместе утеплитель 200 мм и гидробарьер вытесняется парой утеплитель 150 мм и супердиффузионная мембрана. Благодаря таким технологическим приёмам уменьшается стоимость строительства. В дополнение подчеркнём, монтаж кровли упрощается, снижаются трудозатраты, канули в лету контр рейки и дополнительный ярус обрешетки. Супердиффузионная мембрана хранит целостность, комфорт и благополучие всего мансардного этажа. Сегодня многие производители из Европы и Азии поставляют кровельные и фасадные мембраны. У большинства из них близкие эксплуатационные свойства. Отличия можно найти в технологии производства, виде сырья, декоративных добавках, в типе водонепроницаемых плёнок, количестве слоёв, в способе адгезионного скрепления слоёв мембраны. По этому стоимость, качество, функциональность и другие характеристики мембран заметно отличаются. И для строителя, и для владельца
коттеджа важно, чтобы строительные работы проводились быстро и эффективно, а само здание сохраняло исходные качества долгие десятилетия.

Сегодня нам известны несколько типов мембраны, применяемых при возведении кровли и не только в виде подкровельной мембраны.

Виды супердиффузионных мембран для крыши.

Кровельные мембраны применяются в качестве подкровельного покрытия для вентилируемых скатных кровель. Минимальное диффузионное сопротивление мембраны гарантирует быстрый отвод пара наружу. Мембраны обладают высокой прочностью и водо- непроницаемостью.

Пароизоляционная мембрана

Мембраны с «активной пароизоляцией», замедлителями пара, барьерами для пара и т.д., защищают с внутренней стороны утеплитель. От традиционного паробарьера отличаются высокой паропропускной способностью. Количество влаги пропускаемой сквозь такую мембрану в 10 раз больше в сравнении с паробарьером, но в то же время в 10 раз меньше пропускается влага в сравнении с кровельной супердиффузионной мембраной. Такой специфичный материал эффективно работает вместе с утеплителем и кровельной мембраной. Низкое диффузионное сопротивление такого сэндвича делает мансарду дышащей, что значительно увеличивает комфортность микроклимата в жилом помещении.

Так удается избежать в помещении феномена «полиэтиленового кулька». Как легко догадаться, феномен состоит в бесконечном накоплении влаги в жилых и хозяйственных помещениях. Чрезмерная герметичность зданий приводит к закупориванию и отсыреванию. Правильно строить жилые помещения нужно с большой диффузионной активностью ограждающих конструкций.
Активный паробарьер применяется во всём мире, он вытеснил традиционный паробарьер благодаря уникальному микроклимату, который создаётся в жилом помещении.

Гидроизоляция нуждается в способном помощнике. Эффективный отвод влаги из крыши проводит система вентиляции. Для мансарды под скатной крышей эффективна естественная вентиляция, работающая как конвертер. Выглядит это как воздушные каналы от парапета к коньку. Естественные каналы проходят между обрешеткой (под кровельным настилом). Другой способ организации вентканалов получил название: «двойная вентиляция». В первом канале воздух двигается под кровельным настилом, во втором канале под гидробарьером над утеплителем. Получается сдвоенный канал, в котором существуют два потока воздуха: один проветривает пространство под

металлочерепицей, битумной черепицей и т.д., а другой вентилирует пространство между гидробарьером и утеплителем.

Третий способ предполагает применение супердиффузионной мембраны (последнее слово в индустрии кровельных материалов). Мембрана заменяет гидробарьер и благодаря уникальной способности пропускать сквозь каждый квадратный метр своей поверхности по 1,5 литра воды в сутки, избавляет нас от вентканала над утеплителем. Иными словами второй канал совпадает с супердиффузионной мембраной. Ещё важно то обстоятельство, что одинарный вентиляционный зазор на коньке улучшает характеристики энергосбережения для мансарды,утеплитель не охлаждается потоком воздуха.

Однослойная мембрана.

Простейшая супердиффузионная мембрана состоит из однослойного холста. Такой материал обладает минимальным диффузионным сопротивлением, а так же низкой водо- отталкивающей способностью. Применяется только в качестве ветробарьера. Есть попытки создать образец однослойной мембраны с повышенной гидроизоляционной способностью. Холст покрывается импрегнатом. Однако высокого качества покрытия холста получить не удаётся. При сгибании покрытие трескается и теряет поверхностную целостность. К тому же слой импрегната слишком тонкий и не обладает достаточной износостойкостью.

Двухслойная мембрана.

Супердиффузионная мембрана получает высокую гидроизоляционную способность от функциональной полимерной плёнки, которая наноситься на холст как второй слой. При этом сохраняется паропропускающая способность. Такие материалы сохраняют не высокую стоимость и большую популярность как кровельная мембрана. Практика показала, что двухслойные материалы с течением времени получают механические повреждения функциональной плёнки. Так в строительстве появились трёхслойные супердиффузионные мембраны.

Трёхслойная мембрана.

Вершина технологии супердиффузионной мембраны – это трёхслойный материал. Мембрана производиться на основе не тканого холста. В целом состоят из трёх слоёв: основной нетканый волокнистый слой, функциональная плёнка и защитный износостойкой слой. С технологической точки зрения не тканый холст дважды проходит ламинирование.

Как же соединяют слои мембраны? Есть такие варианты: термобондинг, ультрасоник, клеевое соединение. Популярным у производителей стал клеевой способ ламинирования супердиффузионной мембраны. Технологии термобондинг и ультрасоник более совершенные, гарантируют надёжность соединения слоёв и реализуются на дорогом оборудовании.

Гидрозащита крыши – это один из основы факторов, который гарантирует долговечность всего коттеджа. Без надёжной гидроизоляционной способности другие достоинства супердиффузионной мембраны теряют актуальность. Долговечная гидроизоляция достигается правильным выбором материала и соблюдением требований к монтажу. Способность удерживать столб воды высотой 0,5 м обеспечивается функциональной плёнкой в составе мембраны. Встречаются так же материалы производимые по методу гидрофобизирования паропроницаемого холста, однако такие материалы считаются мало эффективными. Последние годы на рынок поступают супердиффузионные кровельные мембраны выдерживающие столб воды в несколько метров (до 5-ти). Такие предложения основываются на данных об износе мембран при эксплуатации. За 15 лет трёхслойная мембрана стирается в двое, это значит, что высокая гидроизоляционная эффективность сохраниться только у мембран с большим запасом прочности.

МЕХАНИЧЕСКАЯ СТОЙКОСТЬ

Удачный исход монтажа супердиффузионной мембраны зависит от механической стойкости материала. Механические повреждения мембраны – это основной риск при монтаже. Для благополучного исхода приходиться либо тщательно заклеивать прорывы, либо использовать более прочные мембраны.

ДИФФУЗИОННОЕ СОПРОТИВЛЕНИЕ: ЧЕМ МЕНЬШЕ, ТЕМ ЛУЧШЕ

Способность пропускать пар – важнейшая задача для кровельной мембраны и основное её отличие от гидробарьера. Высокая паропроницаемость вместе с абсолютной гидроизоляционной способностью открыли уникальные возможности в строительных технологиях, особенно в строительстве мансард и кровель. Диффузионное «открытие» кровельного пирога освобождает здание от излишней влаги. Это означает замедление прогрессирующих изменений в конструкциях, так же предотвращение изменений параметров конструкционных материалов, замедление разрушения. Напомню, что с применением сепердиффузионной кровельной мембраны отпала необходимость в вентиляционном зазоре между «строительной плёнкой» и утеплителем это приводит к прекрасному эффекту: утеплитель а соответственно и вся крыша не охлаждаются. Если быть точным, то надо сказать, что охлаждение замедляется в 3 – 4 раза.

Паропропускающая способность супердиффузионной мембраны измеряется в количестве граммов водяного пара, проходящую через 1 квадратный метр полотна в течении 24-х часов. При этом, проникновение пара происходит естественным образом при температуре окружающей среды 20 градусов. На практике пропускная способность мембраны будет существенно выше, поскольку изнутри кровельного пирога всегда давит тёплый воздух, а над поверхностью супердиффузионой мембраны непрерывно происходит конвекционное движение воздуха. Нужно знать, что единственный честный показатель для оценки эффективности супердиффузионной мембраны – это коэффициент диффузионного сопротивления Sd. Измеряется он в метрах. Речь идёт о величине, которая диффузионно равна слою воздуха. Sd показывает, какой слой воздуха проникает сквозь единицу площади полотна. Чем меньше коэффициент, тем выше способность пропускать пар. Для кровельной мембраны высокого качества Sd составит от 0,015 до 0,04 метра. Для дешевых мембран Sd составит 0,05 и больше метров.

УЛЬТРАФИОЛЕТОВАЯ СТАБИЛЬНОСТЬ

УФ стабильность – относительно важный показатель. Стойкость к УФ лучам необходима для своевременного выполнения строительных работ и обычно составляет 4 – 5 недель. Если мембрану передержать под солнечным светом, можно столкнуться с постепенным снижением термической стойкости кровельной мембраны. Маркировка СЕ на полотне означает, что супердиффузионная мембрана протестирована на стойкость всех эксплуатационных показателей, в том числе и на УФ стабильность. В процессе исследования на кровельную мембрану производят различные виды воздействий, таким образом ускорено воспроизводится многолетний процесс старения материала.

В паспорте мембраны указаны все результаты испытания. По таким данным можно объективно сравнивать и оценивать кровельные мембраны разных производителей. Срок УФ стабильности подразумевает окончание как наружных, так и внутренних работ, то есть нужно осуществить полную изоляцию мембраны от солнечного света. В противном случае облучение материала в течении нескольких лет приведёт к полной или значительной потери свойств на облучаемом участке. Вывод прост: минимизировать время освещения мембраны.

СТОЙКОСТЬ К ПЕРЕПАДАМ ТЕМПЕРАТУР

Часто эту характеристику именуют термоустойчивость супердиффузионной мембраны. На практике это стойкость к температурным колебаниям, которые воздействуют на материал. В летнее время температура на поверхности крыши повышается до +80 градусов. И это в наших широтах! Разогревание супердиффузионной мембраны до температуры 120 градусов оставляет материал в первоначальном состоянии. Однако температурное расширение всех кровельных конструкций может привести к разрушению полотна мембраны. Предотвратить повреждение можно оставляя запас мембраны до 10% при монтаже, иными словами мембраны и плёнки после монтажа свободно висят на стропилах.

Для скатной кровли важны свойства подкровельного покрытия. Этот слой стал вторым щитом или вторым заслоном в противостоянии с силами природы. Этот щит хранит коттедж от проникновения воды будь то по причине задувания атмосферных осадков или по причине выпадания конденсата внутри крыши и стен. Наконец если произошло случайное повреждение целостности кровли второй заслон будет выполнять функции кровли столько, сколько понадобится хозяину коттеджа. Последние двадцать лет популярность строительных плёнок и мембран росла неуклонно. На будущее прогноз однозначен: плёнки и мембраны будут становиться всё лучше, а сфера их применения всё шире.

Диффузионные мембраны. Описание от ПССК

Тема статьи: Строительные мембраны: коротко о главном.

Необходимость применения дополнительных материалов при обустройстве кровли мы освещали в статье «Для чего нужна гидро- и пароизоляция». Рынок строительных материалов не стоит на месте и предлагает более новые, современные варианты решения тех или иных задач.

Именно такими, инновационными, материалами в области обустройства кровли и стен являются диффузионные и супердиффузионные мембраны.
Простыми словами мембраны – это нетканые полотна с микроскопическими порами-воронками, пропускающими пар, но не воду.
Название диффузионная или супердиффузионная мембрана зависит от количества этих самых пор на квадратном сантиметре полотна. Так, диффузионной мембраной называют полотно с частичной (фрагментарной) перфорацией, а супердиффузионной — мембрану с частой (сплошной).
Задача всех строительных мембран в целом – защита строительных конструкций внутренних элементов крыш и стен, а также утеплителя в них от ветра, влаги и подкровельного конденсата, при одновременном выведение пара, из самой конструкции, и как следствие, увеличение срока эксплуатации кровли в целом.
Различают однослойные (например, Наноизол PROF), двухслойные мембраны (Наноизол SM) и многослойные — 3 и более (Наноизол SD).
Однослойные обладают высокой водоупорностью с одной стороны и одновременно высокой паропропускающей способностью, с другой стороны.
Двухслойные — однослойные мембраны, дополнительно армированные полипропиленовым нетканым полотном, который придает материалу бОльшую механическую прочность.
Многослойные, достаточно редки на рынке массового потребления, поскольку предназначены для решения конкретных конструкционных задач.

Благодаря своим свойствам строительные диффузионные мембраны могут заменить несколько слоев классической «многослойной» схемы утепления стен и кровли.
Важным плюсом супердиффузионных мембран, по заявлению производителей, является возможность монтировать их непосредственно на утеплитель без монтажа вентзазора, что позволяет избежать затрат на покупку обрешетки.

Благодаря своему строению, супердиффузионная мембрана позволяет вести монтажные работы при любых погодных условиях, а некоторые даже способны на некоторый период выполнять функции временной кровли (Наноизол PROF). В сравнении с более традиционным, многослойным обустройством утепления кровли и стен, монтаж мембраны более экономичен в плане количества необходимого материала в общем, что при правильном расчете может обойтись дешевле, не смотря на более высокую цену на сам материал.

Разобравшись с назначением нового строительного материала, закономерно возникает вопрос – как правильно монтировать? Производители мембран не придерживаются единообразия, каждая стремиться выделиться и быть узнаваемой, поэтому некоторые окрашивают свою продукцию в разные цвета, другие наносят свой логотип. Однако, эти маркеры не только маркетинговый ход, по технике безопасности правильно, что бы внешняя сторона мембраны была затемнена тем или иным способом. Логика здесь простая – белое или однотонно-светлое полотно будет ослеплять строителей кровельщиков в солнечную погоду. Здесь и кроется секрет правильного монтажа практически любой мембраны – белой стороной к утеплителю, цветной или с надписями – к себе.

Вот так коротко и ёмко мы постарались рассказать то, что необходимо знать о строительных диффузионных и супердиффузионных мембранах. А что лучше и выгодней — многослойное классическое обустройство кровли или же инновационное – решать Вам.

Купить диффузионные мембраны в интернет-магазине

← назад к списку статей и обзоров

11.01.2019, 1475 просмотров.

Строительные супердиффузионные мембраны — ОАО «СветлогорскХимволокно»

Супердиффузионная мембрана — одна из современных и востребованных разновидностей гидро-ветрозащитных мембран. Основная функция — защита утеплителя в конструкции кровли и фасадов от разрушающего влияния внешних факторов (протечки кровли или фасада) и и вывода излишков пара из конструкции здания.

Супердиффузионные мембраны получили свое название за эффективную способность пропускать испарения и одновременно обладать высокими гидроизоляционными характеристиками. Именно вследствие своего состава супердиффузионные мембраны имеют максимально высокие технические характеристики, значительно больше, чем стандартные гидроизоляционные пленки. Для устройства кровли крайне важно, что они могут удерживать давление водяного столба более 1500 мм. вод. ст.

По структуре мембрана представляет собой — внешние два слоя нетканого материала (с УФ-стабилизатором) защищают внутренний слой паропроницаемой пленки (функциональная полипропиленовая «дышащая» пленка, придающая мембране свойства высокой паропроницаемости и гидроизоляции) дублируются ультразвуковым способом скрепления — это и есть структура супердиффузионных мембран. Тогда как обычная гидроизоляционная пленка с микроперфорацией создается путем обычной перфорации (прокола иглами) с частотой 1–2 отверстия на 1 см². Паропроницаемость такой пленки порядка 40 г/м²/сутки, тогда как аналогичный показатель супердиффузионной мембраны более 1000 г/м²/сутки. Как показывает практика реально она составляет 2500–3500 г/м²/сутки, а в совокупности с высоким показателем гидроизоляции (более 1500 мм. вод. столба) обеспечивает 100% защиту утеплителя от промокания и тем самым исключает потерю теплоизоляционных свойств последнего, дополнительно защищая всю конструкцию здания от образования гнили и плесени!

Преимущества применения

Гарантированная защита утеплителя кровли от намокания при протечках основного кровельного или фасадного покрытия;
Свободный выход излишков пара из подкровельных и фасадных систем, с последующим его удалением через вентканалы;
Лёгкость и простота монтажа супердиффузионной мембраны, укладка производится непосредственно на утеплитель без зазора;
Длительный срок службы мембраны и как следствие срок службы всей конструкции дома;
Применение супердиффузионной мембраны обеспечивает значительное улучшение теплоизоляционных свойств всего здания;
Мембрана препятствует пылению волокнистого типа утеплителя, тем самым защищая органы дыхания людей и животных, обеспечивая нормальную экологию. Мембрана состоит из 100% полипропилена, который не вызывает аллергии и не выделяет в обычных условиях вредных веществ.

Назначение, разновидности и технология монтажа гидроизоляционной мембраны FAKRO

Все о гидроизоляционной мембране FAKRO: технические характеристики, преимущества, применение. Как правильно укладывать материал, расчет необходимого количества рулонов и последовательность монтажа.

Мембрана FAKRO EUROTOP – специальный материал, который используется в качестве подкровельной гидроизоляции и для защиты утеплителя от влаги, проникающей под кровлю и фасад дома. Свою популярность мембрана приобрела за счет относительно невысокой стоимости и хороших технических характеристик, которые позволяют использовать ее практически в любых климатических условиях.

Гидроизоляционная мембрана FAKRO – это 3-слойный материал, который состоит из сплошной полимерной пленки, защищенной с обеих сторон слоем нетканого полипропиленового полотна. За счет особой прочности полипропилена FAKRO выдерживает значительные механические нагрузки, перемещение по шероховатой и грубой поверхности во время монтажа. Мембрана выпускается в виде пленки, свернутой в рулон, компактный при хранении и удобный при транспортировке.

Как выглядит гидроизоляционная мембрана FAKRO

Важный параметр гидроизоляционной мембраны – паропроницаемость

Самая важная характеристика гидроизоляционных мембран – способность пропускать через себя пар. Она определяется как количество водяного пара, который за сутки проходит через мембрану площадью 1 м². Именно этот параметр приводится во всех спецификациях материалов, применяемых для гидроизоляции кровли. Благодаря способности пропускать пар мембрана позволяет выводить влагу из теплоизоляционного материала, не давая ей скапливаться на поверхности утеплителя.

Мембрана FAKRO относится к супердиффузионным, поскольку имеет коэффициент паропроницаемости более 1000 г/м² в сутки. В целом классификация мембран по этому критерию выделяет следующие виды:

псевдодиффузионные с паропроницаемостью до 300 г/м²в сутки;
диффузионные – 400-1000 г/м²в сутки;
супердиффузионные – более 1000 г/м²в сутки.

Обратите внимание: считается, что для эффективного удаления влаги из утеплителя паропроницаемость мембраны должна быть не менее 400 г/м²_{в сутки. Для максимально возможной скорости выведения влаги паропроницаемость должна быть больше 1000 г/м² в сутки.}

Приводимая производителем паропроницаемость выступает идеальной, т. е. максимальной (измеряется при комнатной температуре и максимальной разности влажности воздуха по обе стороны от материала). По этой причине было введено понятие рабочей паропроницаемости, которая несколько ниже декларируемой (идеальной), а на практике считают достаточной паропроницаемость более 600 г/м² в сутки.

Еще одна важная характеристика – коэффициент сопротивления диффузии водяного пара

Мембрана FAKRO эксплуатируется в воздушной среде, поэтому ее сопротивление диффузии водяного пара сравнивают с тем же параметром для сухого воздуха. Для этого вводится понятие коэффициента сопротивления диффузии водяного пара. Он отражает, во сколько раз сильнее мембрана сопротивляется прохождению через нее водяного пара, чем такой же слой сухого воздуха.

На практике коэффициент сопротивления диффузии водяного пара не слишком информативен. Поэтому в практических расчетах чаще используют производный от него коэффициент, который называют эквивалентной толщиной сопротивления диффузии водяного пара и обозначают S_d. Его определяют по такой формуле:

S_d = µ · d,

где µ – коэффициент сопротивления диффузии водяного пара, d – толщина мембраны.

S_d измеряется в метрах (м) и в физическом смысле обозначает то, какой толщине воздушного слоя эквивалентна мембрана по ее паропроницаемости. Этот параметр важен при расчете способности пропускать пар многослойных конструкций, к которым относится и утепленная крыша.

Для чего нужна гидроизоляционная мембрана

Утеплитель и внутренние конструкции кровли из-за суточных изменений температур подвергаются образованию конденсата. Он образуется на внутренней стороне кровельного покрытия, после чего начинает скатываться вниз или капать. Вода попадает под кровлю и при сильном дожде или ветре. Влага приводит к преждевременной порче утеплителя – его теплоизолирующие свойства ухудшаются.

Советуем изучить: «Все виды утеплителей: классификация по свойствам и составу».

Расположение гидроизоляционной мембраны в кровельном покрытии

Гидроизоляционная мембрана выполняет несколько функций.

Надежно защищает теплоизоляцию от влаги и атмосферных осадков, предотвращая разрушение материала.
Препятствует выдуванию верхнего слоя утеплителя.
Обеспечивает дополнительное пространство для теплоизоляции за счет того, что может укладываться без устройства второго вентиляционного зазора.

Обратите внимание: мембрана FAKRO за счет устойчивости к УФ-излучению может в течение 3 месяцев выполнять функцию временной кровли. Это становится настоящим спасением в случаях задержки монтажа кровельного покрытия.

Сферы применения мембраны FAKRO

Основное предназначение диффузионной мембраны – гидроизоляция на скатной кровле, межэтажном перекрытии. Материал применяют в каркасном домостроении и при утепленных вентилируемых фасадах. Важным условием правильного действия мембраны выступает выполнение крыши таким образом, чтобы между кровельным покрытием и обрешеткой была обеспечена возможность прохождения вентиляционного воздуха.

В качестве дистанционного слоя под вентилируемой кровлей

В этом случае используется мембрана EUROTOP S265 MaxS. Она выполняет сразу две функции: защищает утеплитель от влаги, которая поступает с вентилируемым воздухом, и служит дистанционным элементом, отделяющим теплоизоляцию так, чтобы обеспечить определенную величину вентиляционного зазора. В качестве дистанционного слоя мембрану используют в совмещенных крышах и в межэтажных перекрытиях из деревянных балок.

Очень часто материал применяют при обустройстве фальцевой кровли. Она близка к плоским крышам (имеет уклон от 3°) и состоит из картин (элементов в виде листов с подготовленной кромкой), соединенных между собой стоячими фальцами.

Как выглядит фальцевая кровля

В фальцевой кровле теплоизоляция монтируется отдельно от покрытия. В основном такая система применяется в крышах, где утеплитель укладывают между балками над жилыми мансардами или на обшивке (цементно-волокнистые плиты, битумная черепица и пр.).

Если ваша кровля имеет уклон более 5°, то для ее безопасной эксплуатации советуем изучить: «Расчет количества снегозадержателей на крышу».

Для уплотнения плит надстропильной теплоизоляции

Здесь гидроизоляционная мембрана защищает соединения досок, фанер и плит OSB, поскольку в стыки между ними тоже может попадать вода. Еще материал хорошо подходит для защиты полиуретановых и PIR-плит.

Применение гидроизоляционной мембраны FAKRO

В качестве ветроизоляционного слоя

Будучи высокопаропроницаемой, мембрана FAKRO часто применяется в качестве защиты от сквозняков каркасных и кирпичных стен, которые утепляют сухим методом на стальной или деревянной сетке.

Но здесь очень важно учитывать способность мембраны пропускать пар в обе стороны, в связи с чем это может вызвать увлажнение. Это наиболее неблагоприятно для каркасных стен, особенно тех, что слабее всего прогреваются (северная сторона) и хуже вентилируются ветром (закрыты другими объектами). В таких ситуациях вместо мембраны рекомендуют использовать ветроизоляцию с низкой паропроницаемостью.

Разновидности гидроизоляционной мембраны FAKRO

Материал классифицируется по плотности, которая влияет на степень паропроницаемости. По этому критерию выделяют:

Отдельно выделяют мембраны с самоклеящимся слоем, который облегчает процесс монтажа материала. В линейке FAKRO с такими свойствами представлены 2 вида мембраны:

Сравнительная таблица характеристик разных видов мембраны FAKRO

Наименование	EUROTOP L2	EUROTOP N15	EUROTOP N35	EUROTOP T-150 с самоклеящимся слоем	EUROTOP T-180 с самоклеящимся слоем	EUROTOP S265 MaxS	THERMOFOL 90 AL
Вес, г/м²	90	115	135	150	180	265	90
Паропроницаемость, г/м² в сутки	3100	2800	2900	1500	1200	–	Непаропроницаема
Продольное сопротивление на разрыв, Н/5 см	200	230	280	350	420	500	250
Допустимая температура эксплуатации	от -40 до +120°С	от -40 до +120°С	от -40 до +120°С	от -40 до +80°С	от -40 до +80°С	от -40 до +120°С	от -40 до +80°С
Класс горючести	Г4	Г4	Г4	Г4	Г4	Г4	Г4
Эквивалентная толщина сопротивления диффузии водяного пара – S_d, м	0,015	0,015	0,015	0,020	0,020	0,020	–
Размеры, м	1,5х50	1,5х50	1,5х50	1,5х50	1,5х50	1,5х30	1,5х50
Устойчивость к воздействию солнечных лучей, месяцы	3	3	3	3	3	3	3

Используя размеры рулонов, можно произвести расчет необходимого количества мембраны или пленки. Для этого площадь, которую требуется гидроизолировать (площадь кровли или фасада), необходимо поделить на площадь одного рулона.

Важно: при расчете необходимого количества рулонов не забудьте учесть необходимость нахлеста полотен. Для этого величину нахлеста (10 см) необходимо вычесть из ширины полотна с обеих сторон – 1,5-0,1-0,1 = 1,3 м. Именно такую ширину и нужно использовать при расчете.

Особый вид продукции FAKRO – пленка THERMOFOL 90 AL

Материал THERMOFOL 90 AL – это 3-слойная пленка, в составе которой присутствуют:

Защитный экран в виде алюминизированного полипропилена, отражающего тепловое излучение.
Полипропиленовая сетка, обеспечивающая материалу прочность.
Полиэтилен, выступающий в качестве последнего слоя.

Подобная пленка подходит для объектов и помещений с высоким уровнем влажности, например, бань. При использовании пленки важно соблюдать ряд правил:

обращать пленку металлизированным слоем в сторону источника водяных паров;
обеспечивать между пленкой и отделкой вентиляционный зазор шириной не менее 4-6 см.

В целом THERMOFOL 90 AL можно использовать для пароизоляции стен и скатных крыш.

Алюминизированная мембрана FAKRO

В чем плюсы гидроизоляционной мембраны FAKRO

Универсальность. Несмотря на разные функции гидро- и пароизоляционных пленок, они считаются взаимозаменяемыми. Это значит, что гидроизоляцию можно использовать в качестве защиты от парообразования под кровлей, а пароизоляцию – для защиты от атмосферных осадков.
Продуманные размеры. Ширина рулона 1,5 м оптимальна для осуществления монтажа. Она минимизирует количество швов.
Возможность укладки в любое время года. Это обусловлено тем, что мембрана и пленка имеют широкий диапазон эксплуатационных температур. Причем технология укладки при разной температуре одинаковая.
Высокая эластичность. Еще одно свойства мембраны, которое обеспечивает простоту ее монтажа. Для закрепления материала поверх теплоизоляции понадобится совсем немного времени, и справиться с этим можно и в одиночку.
Высокая прочность на разрыв. В процессе монтажа исключен риск разрыва мембраны. Это очень важно, поскольку даже небольшое отверстие уже не позволит выполнять пленке свои изоляционные функции.
Длительный срок службы. По окончании устройства кровли вам не придется часто менять гидроизоляцию и тратить на это лишние средства. Необходимость замены возникает только в случае механического повреждения пленки.

Обратите внимание: за счет высокой паропроницаемости мембрану FAKRO можно укладывать внахлест, а еще на всю крышу, включая конек.

Особенности монтажа мембран FAKRO

Укладку мембраны ведут горизонтально, начиная от карниза и двигаясь по направлению к коньку. Полотна укладывают с нахлестом минимум 10 см – можно ориентироваться на пунктирные линии по краю материала (они расположены как раз на расстоянии 10 см от края). На коньке материал можно монтировать и с перехлестом.

Монтаж мембран FAKRO

Для крепления мембраны используют:

Степлер или толевые гвозди – для крепления к несущей системе крыши. Места креплений в дальнейшем, как правило, закрывают контробрешеткой, поскольку они носят технологический характер.
Уплотнительную ленту – для крепления к кровельным конструкциям кровли (каминным трубам, люкам и пр.).
Рейки – для фиксации в полах и перекрытиях. Здесь мембрану крепят к нижней стороне балок или оборачивают вокруг них.

В линейке продукции FAKRO есть специальные соединительные ленты T1020, которые предназначены именно для монтажа пленки. Она обеспечивает плотное примыкание материала к мансардным окнам, каминным трубам и прочим элементам кровли.

В заключение

Супердиффузионная мембрана FAKRO – универсальный материал, который может выступать в качестве паро-, гидро- и ветрозащиты кровли и фасадов, а еще в течение 3 месяцев быть временной кровлей. Мембрана устойчива к низким температурам и солнечному излучению. Материал поставляется в удобной рулонной форме, а еще он прост в монтаже, устойчив к механическим повреждениям. Мембрану можно укладывать на все элементы кровли, в том числе конек, а пленку – использовать в качестве дополнительной защиты бани и прочих помещений с высокой влажностью.

Супердиффузионная негорючая мембрана Изолтекс НГ для утепления кровли

09.07.2012

Компания Аяском предлагает новое применение влагозащитной паропроницаемой негорючей мембраны Изолтекс НГ: в качестве «дышащей» пленки для кровли для влагозащиты утеплителя. Новые плюсы: негорючесть и светостойкость.

Супердиффузионная негорючая мембрана Изолтекс НГ для кровли

Строительные мембраны — это так называемые «дышащие» пленки, которые защищают утеплитель и конструкцию кровли и стены от проникновения атмосферной влаги и не препятствуют выходу внутренних водяных паров. Высокая паропроницаемость или низкое (сопротивление паропроницанию (м²×ч×Па)/мг = 0,012-0,016 по ГОСТ 25898-83) достигается благодаря особой микроструктуре мембран, представляющих собой стеклоткань, пропитанную паропроницаемым составом.

Своим появлением мембраны обязаны ужесточению используемых в западных странах норм теплозащиты строительных конструкций. В России президентом РФ 18.06.2009 г. также предложены меры по повышению энергетической эффективности и энергосбережению. Под энергетической эффективностью зданий понимается свойства зданий и их инженерных систем потреблять лимитированный уровень тепловой энергии, обеспечивая оптимальный внутренний микроклимат помещений.

Негорючие мембраны Изолтекс НГ для утепления кровли

Супердиффузионные негорючие мембраны Изолтекс НГ позволяют наиболее рационально использовать для теплоизоляции все пространство между стропилами. В отличие от других видов пленок, супердиффузионные мембраны укладывают непосредственно на утеплитель, поэтому их применение позволяет отказаться от вентиляционного зазора, который «съедает» до 50% пространства, предназначенного для утепления кровли.

Например, если высота стропил в поперечном сечении составляет 150 мм, то при применении обычных подкровельных пленок толщина утеплителя, который можно уложить между стропилами, составляет около 80 мм. В соответствии с современными требованиями это почти в два раза меньше нормы (70 мм — это минимальный вентиляционный зазор, включая как минимум 20 мм на провисание пленки, и этот зазор необходимо оставить для проветривания утеплителя). Применение супердиффузионной негорючей мембраны для кровли создает дополнительное пространство для теплоизоляции, позволяя уложить утеплитель толщиной 150 мм, равной высоте стропил, что отвечает современным нормам теплозащиты.

Особенно широко дышащие мембраны применяются в мансардном строительстве. Их использование является оптимальным при переоборудовании холодного чердака в мансардное помещение без замены существующей стропильной конструкции.

В отличие от супердиффузионных подкровельных мембран одностороннего применения, которые можно укладывать только определенной стороной вниз, негорючую мембрану для кровли Изолтекс НГ можно укладывать любой стороной.

Супердиффузионные негорючие мембраны Изолтекс НГ применяются как паропроницаемая подкровельная гидроизоляция для защиты подкровельных конструкций, теплоизоляции и чердачного помещения от атмосферной влаги, а также от пыли, копоти и ветра.

Монтаж подкровельной супердиффузионной негорючей мембраны Изолтекс НГ

Подкровельную мембрану Изолтекс НГ необходимо укладывать от краев крыши к ее коньку с нахлестом в обе стороны не менее 10 см в зависимости от уклона крыши. Крепление по длине осуществляется на стропилах оцинкованными гвоздями с плоскими шляпками или скобами механического сшивателя. Дополнительно применяются контррейки на расстоянии не более 1,2 м одна от другой.

Перед укладыванием подкровельной супердиффузионной негорючей мембраны Изолтекс НГ на импрегнированную поверхность необходимо убедиться, что пропитка полностью высохла. Мембрана для кровли Изолтекс НГ устойчива к действию ультрафиолета поэтому может служить временной кровлей без ограничения срока.

Супердиффузионная мембрана для кровли Изолтекс НГ имеет гидрофобную поверхность, с которой капли дождя скатываются, поэтому подкровельную пленку можно монтировать прямо на утеплитель.

Подкровельная мембрана Изолтекс НГ изготовлена на основе стеклоткани, имеет высокую прочность при минимальном растяжении, поэтому между стропилами не образуется провисания пленки.

Супердиффузионная негорючая мембрана Изолтекс НГ не горит, поэтому пожаробезопасные конструкции с применением Изолтекс НГ становятся полностью пожаробезопасны.

Подробное описание и технические характеристики негорючей мембраны для кровли можно посмотреть по ссылке: http://izoltex.ru/product/negoryuchie-membrany/

Что такое супердиффузионная мембрана? Технокровля

Супердиффузионная мембрана — это современный материал, который защищает от внешней влаги утеплитель и внутренние элементы ограждающих конструкций дома.

Для чего используется супердиффузионная мембрана

Супердиффузионная мембрана — удивительный материал, похожий своими свойствами на кожу. Мембраны позволяют утеплителю «дышать», пропуская пар наружу и одновременно не давая проникнуть внутрь случайной влаге (если, например, прохудится крыша).

Из чего состоят супердиффузионные мембраны

Изготавливаются супердиффузионные мембраны из нескольких слоев полипропилена (от двух до четырех). Такая многослойность придает материалу прочность, сохраняя в то же время его гибкость и способность к растяжению. Наружный слой обеспечивает УФ-стабилизацию мембраны, влагооталкиващие, пыле- и ветрозащитные свойства, а внутренний слой — диффузионные качества.

Где применяются супердиффузионные мембраны

Применяют мембраны, при возведении стен и кровли, в так называемых «кровельных (стеновых) пирогах» или «сэндвичах». Незаменимы мембраны в строительстве мансардных помещений, вентилируемых фасадов, могут использоваться в качестве временной кровли. В общем, везде, где требуется гидроизоляция утеплителя.

Диффузионные мембраны: не уступают в прочности супердиффузионным, но, как и пленки, требуют вентиляционного зазора; при его отсутствии забиваются микропоры, и мембрана теряет диффузионные качества.

Супердиффузионные мембраны не нуждаются в зазорах. Их можно крепить сразу на утеплитель, и они не требуют контробрешетки над стропилами. Это существенно сокращает траты при монтаже кровли и утеплении дома, экономит место при возведении стен и кровли.

А еще супердиффузионные мембраны не стоит применять при покрытии крыши ефрошифером, металлической фальцевой кровлей или металлочерепицей без акрилового покрытия. Все эти виды покрытий сильно нагреваются и при суточных перепадах температур образуют много конденсата, с которым по силам справиться лишь специальным антиконденсатным пленкам.

Membrane Dynamics – Krapf Lab

АНОМАЛЬНАЯ ДИФФУЗИЯ И ЭРГОДИЧНОСТЬ В ЖИВЫХ КЛЕТКАХ

Плазматическая мембрана – это переполненная среда, в которой белки и липиды перемещаются в присутствии подвижных и неподвижных препятствий. Кроме того, компоненты мембраны часто взаимодействуют с цитозольными элементами. Мы изучаем динамику потенциалзависимых калиевых каналов Kv2.1 и Kv1.4 и натриевых каналов Nav1.6, используя отслеживание одной молекулы. Путем двойной маркировки каналов GFP и квантовыми точками (QD) мы собираем информацию как об отдельных траекториях молекул, так и о распределении белков в плазматической мембране как ансамбле.

НАРУШЕНИЕ ЭРГОДИЧНОСТИ

Мы анализируем отдельные траектории с точки зрения средних квадратов смещений по времени и по ансамблю. Наши результаты показали, что ионные каналы испытывают аномальную субдиффузию. Мы наблюдаем, что картина диффузии не эргодична в клетках HEK и в нейронах гиппокампа, то есть ансамбль и временное распределение смещений различны. Динамика канала может быть точно смоделирована комбинацией неэргодического случайного блуждания в непрерывном времени (CTRW) и окружающей среды с препятствиями.

ОБЪЕМНАЯ ДИФФУЗИЯ

Диффузия на границах раздела твердое тело – жидкость имеет решающее значение во многих технологических и биофизических процессах. Хотя его поведение кажется обманчиво простым, недавние исследования, показывающие пассивный супердиффузионный перенос, предполагают, что диффузия на поверхности может скрывать огромные сложности. В частности, объемная диффузия происходит, когда молекулы временно высвобождаются с поверхности для выполнения трехмерных переходов в объем жидкости. Это явление имеет дихотомию, когда молекула всегда возвращается на поверхность, но средняя длина скачка бесконечна.

ПУБЛИКАЦИИ

Weigel et al. «Эргодические и неэргодические процессы сосуществуют в плазматической мембране, что наблюдается при отслеживании одиночных молекул», PNAS 108, 6438 (2011)

Weigel et al. “Анализ диффузионного пропагатора для отслеживания одиночных частиц”, Phys. Rev. E 85, 041924 (2012)

Krapf, «Механизмы, лежащие в основе аномальной диффузии в плазматической мембране», Current Topics in Membranes 75, 167 (2015)

Campagnola et al., «Супердиффузионное движение нацеленных на мембрану доменов C2. ”, Sci.Rep.5, 17721 (2015)

Krapf et al. «Странная кинетика объемной диффузии на липидных бислоях», Phys. Chem. Chem. Phys. 18, 12633 (2016)

A. Weron et al. «Нарушение эргодичности на поверхности нейронов возникает в результате случайного переключения между диффузными состояниями», Sci. Rep.7, 5404 (2017)

G. Sikora, A. Wyłomańska, J. Gajda, L. Solé, E.J. Акин, М. Тамкун и Д. Крапф, «Выявление различных популяций ионных каналов на поверхности нейронов гиппокампа с помощью анализа повторяемости отслеживания одиночных частиц», Phys.Ред. E 96, 062404 (2017)

Д. Крапф и Р. Метцлер, «Странная межфазная молекулярная динамика», Physics Today 72, 9, 48 (2019)

A. Sabri, X. Xu, D. Крапф, М. Вайс, “Выяснение происхождения гетерогенной аномальной диффузии в цитоплазме клеток млекопитающих”, Phys. Rev. Lett. (в печати, 2020)

СОТРУДНИКИ

Кшиштоф Бурнецки, Гжегож Сикора, Майк Тамкун, Маттиас Вайс, Александр Верон, Агнешка Выломаньска

Мембраны

0 Не-броуновская диффузия 949 •

Концепции аномальной диффузии

•

Аномальная диффузия в липидных бислоях

•

Эргодическая вязкоупругая диффузия в жидких неупорядоченных, упорядоченных и гелевых фазах

•

Неравномерная диффузия по Гауссу в переполненных липидных бислоях

•

Дефекты мембраны из-за стержневидных адсорбированных объектов

Abstract

Динамика компонентов и поверхностный отклик клеточных мембран – также в связи со связыванием различных частиц и макромолекул с ними. мембрана – до сих пор вызывает споры в сообществе мембранной биофизики, особенно в отношении переполненных мембран живых биологических клеток.Здесь мы рассматриваем недавние эксперименты по отслеживанию одиночных частиц в плазматических мембранах живых клеток и суперкомпьютерные исследования липидных двухслойных модельных мембран с белковой краудингом и без него. Особое внимание уделяется наблюдению аномальной неброуновской диффузии как липидных молекул, так и белков, встроенных в липидный бислой. В то время как однокомпонентные чистые липидные бислои в симуляциях демонстрируют только временную аномальную диффузию липидных молекул в наносекундных временных масштабах, стойкость аномальной диффузии становится значительно более длительной при добавлении беспорядка – за счет добавления холестерина или белков – и при прохождении мембранные липиды в гелевую фазу.Одновременно с этим эксперименты демонстрируют аномальную диффузию встроенных в мембрану белков вплоть до макроскопических временных масштабов в минутном временном диапазоне. Особое внимание будет уделено физическому характеру аномальной диффузии, в частности возникновению старения, наблюдаемому в экспериментах – эффективный коэффициент диффузии измеренных частиц является убывающей функцией времени. Кроме того, мы представляем результаты для зависящего от времени локального масштабного показателя среднего квадрата смещения наблюдаемых частиц.Сообщается о недавних результатах, обнаруживающих отклонения от общепринятых гауссовых моделей диффузии в мембранах, переполненных белками. Свойства автокорреляционной функции смещения липидных молекул обсуждаются в свете соответствующих физических моделей аномальной диффузии, как для не переполненных, так и для переполненных мембран. В последней части этого обзора мы обращаемся к грядущей области искажения мембраны за счет удлиненных частиц, связывающих мембрану. Мы обсуждаем, как компартментализация мембраны и энергия связи частицы с мембраной могут влиять на динамику и реакцию липидных мембран.Эта статья является частью специального выпуска, озаглавленного: Биомоделирование под редакцией Илпо Ваттулайнен и Томаш Рог.

Ключевые слова

Липидный бислой

Белковый краудинг

Аномальная диффузия

Моделирование

Стохастическое моделирование

Негауссовские процессы

Рекомендуемые статьиЦитирующие статьи (0)

Посмотреть аннотацию

Цитирующие статьи

Frontiers | Аномальная субдиффузия в живых клетках: устранение разрыва между экспериментами и реалистичными моделями посредством совместных задач

1.Введение

Жизнь клетки определяется высокодинамичными микроскопическими процессами, происходящими в различных пространственных и временных масштабах от отдельных макромолекул до органелл. Оптическая микроскопия позволила четыре десятилетия назад первые измерения движения биомолекул в клетках. Сначала путем восстановления флуоресценции после фотообесцвечивания (FRAP) [1] и флуоресцентной корреляционной спектроскопии (FCS) [2], а в последнее время с помощью отслеживания отдельных частиц (SPT) [3, 4]. Несколько факторов объединили усилия, чтобы популяризировать эти методы во многих биофизических и биологических лабораториях: (i) разработка высокочувствительных детекторов, (ii) появление генетически кодируемой флуоресцентной маркировки белков в конце 90-х годов [5-7] и (iii) появление в 2000–2010 гг. микроскопии сверхвысокого разрешения в дальней зоне [8–12].Все эти технологические усилия предоставили нам доступ к мониторингу молекулярного движения в клетках с беспрецедентным пространственным (вплоть до отдельной молекулы) и временным разрешением [13, 14]. Принятие этих методов имело первостепенное значение в продвижении понимания клеточной организации и динамики [15-17].

Хотя получение достаточных наборов экспериментальных данных раньше было ограничивающим фактором, эти технологические достижения в сочетании с распараллеливанием сбора данных обеспечивают в настоящее время огромные объемы данных, доступных для анализа молекулярного движения внутри клетки.В свою очередь, богатство этих данных раскрыло непредвиденную сложность и разнообразие механизмов движения биомолекул в клетках. Поэтому много усилий уделяется анализу данных, предоставленных FCS или SPT, с использованием прямого подхода или метода вывода.

Однако выбор подходящих алгоритмов для анализа сложности наблюдаемых явлений по-прежнему остается важной проблемой. Действительно, обилие экспериментальных данных часто затрудняет определение того, какие физические модели следует рассматривать, а какие соответствующие биофизические параметры следует оценивать на их основе.Мы рассматриваем и решаем эту проблему с этой точки зрения.

Сначала мы кратко рассмотрим ключевые модели аномальной диффузии, относящиеся к клеточной биологии, и вкратце опишем некоторые из существующих методов либо для определения параметров модели, либо для выполнения выбора модели. Мы обсудим актуальность численного моделирования и важность разработки реалистичных наборов данных, близко имитирующих результаты, полученные в экспериментах на биологических образцах. Мы также подчеркнем часто упускаемые из виду ограничения в существующих методах сбора данных и подчеркнем роль экспериментального шума и смещения вышеупомянутых методов.Наконец, мы представим и будем выступать за разработку всеобъемлющих наборов смоделированных данных и показателей, позволяющих сообществу объективно оценивать существующие и новые инструменты анализа. Мы надеемся, что эта работа вызовет открытую дискуссию об ограничениях и проблемах анализа и моделирования диффузии молекул в сложной среде клетки.

2. Броуновское против аномальной диффузии

Возможно, одним из наиболее известных результатов теории броуновской диффузии является то, что средний квадрат смещения (MSD) случайного блуждающего человека линейно масштабируется со временем и пропорционален коэффициенту диффузии жидкости, в которой происходит диффузия.Поскольку x ( t ) является положением случайного блуждающего в момент времени t (в одном измерении), это означает, что MSD 〈 x ( t ) ²〉 = 2 Dt , где 〈·〉 обозначает усреднение по ансамблю и x (0) = 0. Однако броуновская диффузия не объясняет физику неупорядоченных систем. Интересно, что повсеместное наблюдение в клеточной биологии состоит в том, что диффузное движение макромолекул и органелл является аномальным, то есть изменение MSD со временем обычно характеризуется сублинейным увеличением.В большинстве случаев это сублинейное увеличение MSD со временем может быть подогнано к степенному соотношению 〈 x ( t ) ²〉 ∝ t ^α с показателем α <1, что оправдывает слово «субдиффузия». Субдиффузию обычно связывают с скоплением клеток, пространственной неоднородностью или молекулярными взаимодействиями. Другой возможностью аномальной диффузии является супердиффузия с 1 <α <2. Действительно, многие процессы в биологии демонстрируют активный перенос или комбинации активных и случайных движений.

Таким образом, аномальная диффузия в клетках является очень активной областью исследований, включающих биофизику, клеточную биологию, статистическую физику и математическое моделирование.

Столкнувшись с набором данных, полученных из экспериментов FCS или SPT, первый вопрос, на который нужно ответить, заключается в том, действительно ли измеренная субдиффузия является проявлением аномального процесса. Часто комбинация нескольких нормальных механизмов диффузии или экспериментальных артефактов приводит к кажущейся диффузии.Если аномальная субдиффузия – характеризуемая степенным законом масштабирования MSD со временем – может быть идентифицирована, установление физической модели, лежащей в основе процесса диффузии, может пролить свет на молекулярные механизмы, управляющие движением интересующей молекулы.

Ниже мы сначала сосредоточимся на трех классических моделях аномальной субдиффузии и их общей биологической интерпретации, а именно модели случайного блуждания в непрерывном времени (CTRW), модели дробного броуновского движения (fBm) и случайных блужданий по фрактальным и неупорядоченным системам ( обзор см. в e.g., [18]), затем мы кратко опишем различные модели, охватывающие процессы супердиффузии, которые могут встречаться в клетках, такие как модель бега и падения, полеты Леви и супердиффузионные fBm.

Модель случайного блуждания в непрерывном времени Модель является обобщением случайного блуждания, в котором диффундирующая частица ждет случайное время между прыжками. В более общем плане, когда распределение ϕ (τ) времени ожидания τ является длиннохвостым и не может быть усреднено (например, ϕ (τ) ∝ τ ^{– (1 + α)} и 0 <α <1), ансамбль -среднее MSD показывает аномальное масштабирование со степенным законом.Прямая интерпретация CTRW в контексте молекулярной биологии ассимилирует время ожидания взаимодействиям молекулы с неподвижным субстратом (в соответствующих временных и пространственных масштабах). Важно отметить, что взаимодействие с характерным временем пребывания не соответствует условиям модели. Интересно, однако, что распределение времени ожидания неспецифических взаимодействий, в большом количестве в клетке, может быть не усредняемым и, таким образом, CTRW является хорошей микроскопической моделью для одного типа аномальной субдиффузии в клетке. Было предложено управлять цитозольной диффузией наноразмерных объектов в клетках млекопитающих [19], а также его использовали для объяснения бокового движения калиевых каналов в плазматической мембране клеток [20].

Модель дробного броуновского движения – это другое обобщение броуновской диффузии, в котором скачки между временами запаздывания следуют нормальному распределению, но учитывают корреляционную функцию, заданную формулой 〈 x ( t ) x ( s ) 〉 = 1/2 ( t ^{2 H} + s ^{2 H} – ( t – s ) ^{2 H}) для t > s > 0.Таким образом, процесс fBm характеризуется индексом Херста H в диапазоне от 0 до 1. Значение H определяет тип скачкообразной зависимости в процессе fBm, так что H > 1/2 указывает на положительную корреляцию. между приращениями броуновское движение достигается для H = 1/2, а приращения имеют отрицательную корреляцию, когда H <1/2. СКО для fBm определяется как 〈 x ( t ) ²〉 t ^{2 H}, что, опять же, включает броуновскую диффузию для H = 1/2 и дает субдиффузию для H <1/2 или супердиффузия для H > 1/2 (см. ниже).Модель fBm точно описывает диффузию частиц в вязкоупругой жидкости [21], и часто утверждается, что молекулярное скопление в клетке приводит к микровязкости и, следовательно, к аномальной диффузии. Она была предложена в качестве модели диффузии теломер в ядре [22, 23].

Другой возможной моделью аномальной диффузии в ячейке является модель случайных блужданий во фрактальных средах и неупорядоченных системах . Фракталы – это самоподобные математические объекты, построенные на повторении простых правил и характеризующиеся нецелым числом: фрактальной размерностью .Хотя все еще ведутся дискуссии, некоторые авторы предположили, что организация хроматина следует, как приближение первого порядка, фрактальной структуре, и были предложены оценки его фрактальной размерности [24]. Случайные блуждания по фракталам являются субдиффузионными из-за пространственной корреляции смещений, а коэффициент масштабирования по степенному закону МСД со временем равен 2/ d _w, где d _w – коэффициент Размерность прогулки , специфичная для фрактала.Хотя уместность модели фрактальной сети для описания молекулярной диффузии все еще обсуждается, оправдана попытка интегрировать многомасштабные характеристики клеточной организации в такую фрактальную модель.

Среди существующих супердиффузионных движений в клетках есть процесс «беги и падай», который состоит из чередующихся фаз быстрого активного и медленного пассивного движения, приводящего к временной аномальной диффузии [25]. Первоначально наблюдаемый для движения бактерий, он недавно был использован для описания молекулярных движений в клетках, таких как движение моторов по филаментам цитоскелета.Моторные белки выполняют ряд шагов (запускаются), пока они случайным образом не отсоединятся от филаментов и не диффундируют в переполненной цитоплазме (вращение) перед повторным связыванием [26]. То же самое может означать факторы транскрипции в ядре, которые ищут свой кодон инициации, чередуя последовательную диффузию и одномерное скольжение по ДНК. Супердиффузионная fBm, которая характеризуется индексом Херста H > 1/2, была описана как внутриклеточное движение частиц в сверхнаполненной цитоплазме amibae [27].Наконец, полеты Леви ранее были предложены для внутриклеточного транспорта на основе актина, опосредованного молекулярными моторами [28], а недавно и в случае мембраны, нацеленной на белок C2 [29].

Отметим, что описанные выше модели никоим образом не охватывают исчерпывающим образом диапазон моделей, которые, как известно, демонстрируют аномальную диффузию (см., Например, [30–32]). Однако CTRW, fBM и случайные блуждания во фрактальных моделях были тщательно изучены; Что еще более важно, они могут сопоставить параметры модели с соответствующими биологическими и биофизическими характеристиками. Поэтому мы ограничим наше обсуждение вышеупомянутыми случаями и тем, как их можно использовать для анализа и интерпретации экспериментальных данных, полученных с помощью FCS и SPT.

3. Какие методы правильно анализировать диффузионный процесс?

3.1. Флуоресцентная корреляционная спектроскопия

Принцип FCS заключается в измерении временных изменений молекулярной концентрации в заданном месте в объеме биологического образца. Это достигается путем отслеживания временных флуктуаций сигнала флуоресценции, испускаемого молекулами, присутствующими в объеме наблюдения, который возбуждается сфокусированным лазером.Основное предположение FCS состоит в том, что система находится в динамическом равновесии, и поэтому флуктуация сигнала может быть коррелирована с диффузией молекул в пределах объема наблюдения. В то время как амплитуда колебаний связана с количеством молекул в объеме наблюдения, затухание их автокорреляции во времени зависит от их подвижности.

Типичная установка FCS состоит из осветительного лазера и конфокального микроскопа с быстрым одноканальным однофотонным детектором.Лазерный луч освещает детектируемый объем с обычно гауссовым профилем интенсивности и возбуждает флуорофоры в фокальном объеме. Излучаемый флуоресцентный свет улавливается детектором и зависит от колебаний локальной концентрации меченых молекул.

Параметры, такие как среднее количество молекул (N) и их среднее время пребывания (τ _d) в конфокальном объеме (поверхности), могут быть получены либо непосредственно из измерения флуктуации интенсивности флуоресценции, либо косвенно с помощью временного автоматического -корреляция этого колебания.Второй метод является наиболее популярным для анализа данных FCS (см. Рисунок 1). Основным недостатком стандартной FCS является отсутствие прямого мониторинга возможных пространственных и / или временных неоднородностей, которые могут привести к отклонению от чисто броуновского движения. Было предложено несколько подходов для решения этой проблемы, включая точечную вариацию FCS (sv-FCS) [14, 33], FCS с линейным сканированием и STED-FCS [34, 35], а также подходы к визуализации, такие как (пространственно) -временной корреляционная спектроскопия с визуализацией [(S) TICS], растровая корреляционная спектроскопия с визуализацией (RICS) [36] или, в последнее время, FCS с визуализацией всей плоскости (Im-FCS) [37]. С развитием коммерческих микроскопов в сочетании с возможностями FCS этот метод и его производные в настоящее время становятся все более популярными в биологических лабораториях.

Рисунок 1 . Схематическое изображение типичной установки, используемой в экспериментах по флуоресцентной корреляционной спектроскопии (A) и отслеживанию одной / нескольких частиц (B) . (A) Лазер фокусируется на флуоресцентно меченом образце объективом микроскопа. Затем флуоресценция улавливается объективом и конфокально фокусируется (с использованием точечного отверстия) на детекторе счета одиночных фотонов (лавинный фотодиод, APD).Этот детектор регистрирует флуктуацию флуоресцентного излучения в конфокальном объеме образца. Прямая ссылка на электронный коррелятор разрешает онлайн-генерацию автокоррелограммы. (B) Лазер фокусируется в задней фокальной плоскости объектива микроскопа, чтобы получить полное освещение поля образца. Флуоресценция, испускаемая каждой отдельной частицей, присутствующей в поле освещения, затем напрямую отображается на чувствительной камере (устройство с зарядовой связью, CCD).Получается фильм, и постобработка этого фильма позволяет отслеживать отдельный излучатель, а затем генерировать среднеквадратичное смещение (MSD) как функцию кривых времени задержки.

Был исследован широкий диапазон динамических процессов, приводящих к колебаниям концентрации (т.е. диффузия, поток, химические реакции и их различные комбинации), для получения соответствующих аналитических выражений временной автокорреляционной кривой G ( t ) в случае гауссовой (лазерной конфокальной) геометрии освещения / детектирования (обзор см. в [38] и ссылки в ней).Например, в случае броуновского движения в 2D, G (t) = 1 / {N̄ (1 + 4Dt / w2)}, где w – размер перетяжки пучка, а N – среднее количество молекул в объем наблюдения. Основной подход к идентификации и количественной оценке диффузионного процесса в FCS состоит в нелинейной аппроксимации методом наименьших квадратов экспериментальных автокорреляционных кривых с использованием описанных выше аналитических выражений и различении этих моделей, которые лучше всего подходят, с использованием различных статистических тестов. Хотя он может предоставлять количественные значения параметров статистически выбранной модели движения, он может быть сильно смещен, особенно для сложных движений.Байесовский подход к анализу коррелограмм FCS для отдельных точек был предложен для различения различных моделей без предвзятости [39, 40].

Другой способ различать разные типы движения – исследовать пространство и время с помощью FCS, например, с использованием svFCS. svFCS предлагает возможность генерировать так называемые «законы диффузии» путем построения графика изменений времени пребывания (τ _d) как функции исследуемой поверхности (то есть лазерной перетяжки) w ².Это позволило напрямую идентифицировать отклонения от чисто броуновского движения в плазматической мембране клеток [41] или аномальную диффузию, происходящую либо во время липидного фазового перехода первого рода [42], либо в негомогенных жидкостях, гелях и плотных растворах [43, 44]. ]. Недавно он был расширен до STED-FCS со строчной разверткой [45] и Im-FCS [46].

3.2. Отслеживание одиночных / множественных частиц

Хотя концентрация подмножества флуоресцентных молекул в конфокальном объеме в экспериментах с FCS близка к режиму с одной молекулой, измерение измеряет среднее движение ансамбля молекул, диффундирующих в точку наблюдения и из нее.И наоборот, SPT по своей конструкции является подходом с одной молекулой, отслеживая, таким образом, движение отдельных молекул. Одна из сильных сторон SPT – это возможность фиксировать редкие события или поведения, которые в противном случае были бы скрыты в пределах среднего.

Принцип SPT-экспериментов прост: он заключается в извлечении изменений положения отдельных молекул в интересующем образце, то есть временного ряда двумерных или трехмерных координат местоположения молекулы.Это достигается в два этапа: во-первых, путем оценки центроида измеренной функции рассеяния точки (PSF) каждого обнаруженного отдельного излучателя, а во-вторых, путем связывания траектории одной и той же молекулы между последовательными изображениями. Важно отметить, что точность, с которой можно точно определить положение молекулы, зависит только от отношения сигнал / шум измеренной PSF, что позволяет получить субволновую точность обычно порядка ~ 10 нм.

Базовая экспериментальная установка SPT состоит из возбуждающего лазера, объектива с высокой числовой апертурой, набора дихроичных и фильтров для разделения длин волн возбуждения и излучения, линзы трубки и высокочувствительной камеры, способной обнаруживать отдельные флуорофоры (см. Рисунок 1). .Лазер фокусируется на задней фокальной плоскости объектива, чтобы получить конфигурацию освещения с широким полем, которую можно настроить на полное внутреннее отражение (TIRF) или сильно наклонное освещение (HILO) [47] для увеличения отношения сигнал / шум при изучении молекулярной динамики. в клеточных мембранах или внутри клеток соответственно. Флуоресцентный свет собирается тем же объективом, а изображение одиночных излучателей формируется на плоскости камеры через линзу трубки [13, 48].

Объем полученной информации о биологической системе из анализа SPT зависит от характера эксперимента.Изучение медленно диффундирующего трансмембранного белка даст гораздо более длинные следы, чем быстро диффундирующий фактор транскрипции в ядре. В последнем случае следы будут ограничены количеством изображений, на которых отслеживаемая частица остается в пределах глубины фокуса вокруг плоскости изображения, в отличие от первого случая, когда фотообесцвечивание является ограничивающим фактором.

Классический анализ набора траекторий заключается в вычислении зависимости MSD (среднего по времени или среднего по ансамблю) с течением времени от распределения скачков при увеличении времени запаздывания, определяемого захватом камеры, обычно порядка десятков РС.Однако, как мы увидим в следующем разделе, были предложены различные подходы и оценки для того, чтобы анализировать и интерпретировать данные SPT в полной мере. По сравнению с FCS, анализ SPT интенсивно исследуется, и можно выделить несколько семейств методов (см. Также обзоры: [24, 49, 50]). В области случайных процессов вывод коэффициента диффузии из отобранного процесса является общей проблемой (см., Например, [51, 52]). Однако эту теорию нельзя применить при переходе к экспериментальным траекториям, и были предложены другие подходы.

3.2.1. Методы на основе MSD

Первое семейство алгоритмов анализа SPT пытается выполнить надежный вывод MSD. Использование MSD для изучения диффузии было введено Эйнштейном в 1906 году и возрождено в биологии [53]. Анализ MSD может быть выполнен либо путем вывода коэффициента диффузии из одной траектории (настройка, изученная в [54]), либо путем объединения различных траекторий [55], и было предложено множество уточнений и оценок, основанных на MSD [56, 57] .

При выводе кинетических параметров из серии отдельных траекторий возникает проблема, что для обычных длин траекторий, полученных в ядерной СПД (длина << 20 точек на трек) и общей ошибки локализации, неточность может достигать 100% [54, 58] .Таким образом, любой подход, который использует MSD на коротких траекториях, следует оценивать с большой осторожностью. Для более длинных траекторий (таких как диффузия в мембране) были предложены подходы, которые могут сегментировать траектории в зависимости от типа движения [59].

3.2.2. Скрытые марковские модели (HMM)

Второе семейство алгоритмов анализа SPT основано на марковских моделях и скрытых марковских моделях. Большинство из них были получены для выполнения классификации сегментов траектории, при этом предполагаемая скрытая переменная являлась состоянием диффузии или текущим коэффициентом диффузии.Например, Monnier et al. [60] вводит метод HMM-Bayes, чтобы сделать вывод о том, находится ли сегмент траектории в одном (или нескольких) диффузионных или активных транспортных состояниях. Более того, Slator et al. В [61] реализован вывод шума локализации для определения переключений коэффициента диффузии в пределах одной траектории. Аналогичный подход был использован для обнаружения конфайнмента [62].

Эти методы часто основываются на фиксированном количестве состояний, что связано со значительными математическими ограничениями. Некоторые из этих ограничений были преодолены с помощью так называемого вариационного байесовского вывода [63].Прототипом алгоритма, выполняющего вариационный байесовский вывод на HMM, является vbSPT [64]. Этот алгоритм может оценивать количество диффузных состояний и постепенно объединять увеличивающуюся информацию об этих состояниях по мере анализа траекторий. Алгоритм был дополнительно доработан, чтобы включить оценку ошибки локализации [65].

3.2.3. Вывод карт коэффициентов диффузии

Третье семейство алгоритмов анализа SPT не только выводит коэффициент диффузии по популяции диффундирующих молекул, но также и пространственную карту диффузии [66, 67].Этот подход был впервые применен в мембранах, где можно легко получить высокую плотность треков. Расширение этого подхода с использованием сверхзатухающего уравнения Ланжевена движения одиночной молекулы пролило новый свет на сборку ВИЧ-1 в живых клетках [68]. Эти многообещающие методы не тестировались, кроме мембранных молекул, но высокие коэффициенты диффузии свободно диффундирующих клеточных белков могут затруднить построение такой карты. Более того, в отличие от мембран, белки могут находиться в одном месте с разными коэффициентами диффузии, в зависимости от того, взаимодействуют ли они с данной структурой или нет.

3.2.4. Вывод аномальной диффузии

Было предложено множество подходов к выводу об аномальной диффузии в клетках; обзор некоторых из них можно найти в Guigas and Weiss [69]. Можно использовать прямой метод, подгоняя МСД по степенному закону для оценки коэффициента аномальной диффузии α. Однако были предложены альтернативные методы, многие из которых были сосредоточены на выводе параметров, специфичных для модели, или на методах различения типов аномальной диффузии.

Было предложено несколько методов для определения параметров диффузии для нескольких моделей аномальной диффузии. Для случая диффузии в неупорядоченных (фрактальных) средах Шкилев [70] предлагает оценки, которые могут быть применены к SPT, FCS и FRAP. Для случая дробного броуновского движения были предложены методы вывода как аномального коэффициента диффузии (α), так и обобщенного коэффициента диффузии ( D _α). Первый подход [71] учитывает шум (ошибку локализации) и дрейф и использует байесовский вывод. Последний [72] основан на квадрате смещений и использует метод наименьших квадратов для оценки D _α.

И наоборот, вместо того, чтобы пытаться оценить параметры известной модели, ключевой вопрос состоит в том, чтобы провести различие между различными моделями аномальной диффузии. В прототипном подходе [73] использовался байесовский вывод для различения броуновской, аномальной, ограниченной и направленной диффузии, а также использовались пропагаторы, связанные с каждой отдельной моделью диффузии. Однако Hellmann et al. [74] с помощью моделирования обнаружили, что очень трудно отличить fBm от диффузии на фрактале, когда присутствует шум локализации, как в SPT, так и в FCS.Авторы использовали комбинацию методов для вывода, включая методы MSD и p -variation. В Burnecki et al. [23] авторы предлагают серию тестов для «однозначной» идентификации fBm, последовательно доказывая, что несколько других моделей ошибочны. Были предложены другие тесты для отличия fBm от CTRW с использованием теста, основанного на p -вариантах [75]. Вариации p представляют собой конечную сумму p -й степени приращений траектории.Наконец, подходы к выводу среднего времени первого прохождения частицы использовались, чтобы различать CTRW и диффузию во фракталах [76, 77].

Было предложено много других семейств методов для определения типов диффузии. Некоторые полагались на оценки максимального правдоподобия [78], автокорреляционные функции [79] или более экзотические оценки [80]. Еще одна линия прогресса была достигнута в типе моделируемых моделей. Напр., Amitai [81] представил модель, в которой TFs могут связываться и повторно связываться в плотной хроматиновой сетке.Эта модель была последовательно адаптирована для объяснения аномальной диффузии динамики CTCF [82].

Наконец, отметим, что многие модели были разработаны для вывода потенциала улавливания в мембранах (например, [83, 84]). Мы не рассматриваем их здесь, поскольку их применение ограничивается мембранами.

3.3. Сильные и слабые стороны двух техник

Сильным ограничением является то, что экспериментальный контекст, либо в FCS, либо в SPT, может привести к ложному определению аномальной диффузии.Другими словами, конкретные экспериментальные параметры (низкая статистика, шум местоположения, пространственное ограничение и т. Д.) И / или несоответствующий анализ данных могут привести к неправильному выводу, что показатель диффузии α 1. Эти артефакты касаются как SPT [85], так и FCS [43]. Это, например, случай, если α определяется подбором MSD или автокорреляцией со временем, а статистическая мощность низкая (низкая выборка временных точек или короткие траектории в SPT, низкий сигнал / шум на малых или больших временах в FCS).Чтобы избежать таких предостережений, при выборе модели необходимо использовать более сложные подходы, чтобы однозначно продемонстрировать и охарактеризовать лежащий в основе сложный процесс распространения.

Пока что большинство инструментов вывода, доступных в литературе, лишь частично учитывают смещения, описанные выше, и обычно ограничены в терминах моделей аномальной диффузии, которые они рассматривают. Например, в Hansen et al. [58] авторы показали, что алгоритм, не учитывающий ошибку локализации, может неправильно оценивать коэффициенты диффузии.Точно так же тот факт, что наблюдаемые белки диффундируют в замкнутом объеме, приводит к сублинейной MSD, явлению, которое широко задокументировано и которое необходимо принимать во внимание, чтобы правильно различать истинную аномальную диффузию и простой эффект ограничения. Точно так же ошибки отслеживания (неправильные связи между дорожками) также могут выглядеть как аномальная диффузия.

Некоторые из этих смещений можно минимизировать на этапе сбора данных (например, за счет использования высокой частоты кадров и низкой плотности маркировки [58]), другие необходимо явно учитывать в модели.На сегодняшний день большинство доступных алгоритмов вывода не сравнивались с реалистичными условиями визуализации. Кроме того, до сих пор отсутствует общий реалистичный алгоритм вывода.

4. Заключение: необходимость контролируемых показателей

Столкнувшись с разнообразием описанных выше подходов, хотелось бы узнать производительность каждого подхода на типичных репрезентативных наборах данных. Чтобы сравнение было справедливым, для этого требуются два основных компонента: (i) наличие эталонного набора данных или эталонного теста – возможно, одного эталонного набора данных для каждого основного класса экспериментальных методов и (ii) честного, объективного, прозрачного и открытого сравнения. процесс, с наборами данных, процедурами сравнения и результатами, которые четко сформулированы и общедоступны.В нескольких областях информатики использовались открытые соревнования сообщества для организации процесса и создания открытых тестов для сообщества. Компьютерное зрение, прикладное машинное обучение или прогнозирование временных рядов, среди многих других, имеют давнюю традицию использования этих соревнований. Эта стратегия оказалась широко успешной, поскольку она распараллеливает исследования огромного сообщества высококвалифицированных исследователей. Для этой цели даже доступны интернет-платформы или службы, в том числе, среди многих других, Kaggle (www.kaggle.com) или DrivenData (www.drivendata.org). Это еще больше увеличивает размер конкурирующего сообщества и разнообразие предложений. Фактически, помимо предоставления базовых наборов данных и критериев, открытые конкурентные вызовы также могут способствовать появлению радикально новых подходов к открытой проблеме. Многие из этих конкурентных проблем связаны с биомедицинскими приложениями (например, http://dreamchallenges.org или https://grand-challenge.org), в том числе некоторые из них связаны с микроскопией (см.г., https://cremi.org). Недавно в серии последовательных общественных соревнований по визуализации одиночных молекул участвовали десятки лабораторий и были сосредоточены на алгоритмах отслеживания [86], а также 2D и 3D локализации для сверхвысокого разрешения [87]. Наконец, недавно была поставлена еще одна задача – вывести показатель аномальной диффузии по траекториям частиц (http://www.andi-challenge.org/) [88].

На практике важной особенностью соревновательных задач является предоставление размеченных примеров данных, которые участники смогут использовать в качестве обучающей выборки.Действительно, согласно стандартной практике машинного обучения, этот обучающий набор данных должен отличаться от набора тестов, который включает данные, используемые для оценки производительности алгоритма. Поэтому организаторы обычно публикуют два набора данных (обучающий набор данных и тестовый), из которых только обучающий набор данных поставляется с меткой каждого примера – только организаторы знают истинную метку тестового набора данных. После обучения результаты испытания основаны на некоторой количественной оценке производительности инструментов участников на тестовом наборе, хотя производительность на обучающем наборе также может быть сообщена как способ оценки возможностей перетренированности / обобщения.Однако во многих случаях невозможно предоставить «истинную» метку экспериментальных данных, потому что такого золотого стандарта не существует. В этом случае компьютерное моделирование может использоваться для генерации синтетических данных, если это моделирование достаточно реалистично, чтобы производительность алгоритмов не отличалась от их производительности при реальных экспериментальных измерениях. В недавних задачах сверхвысокого разрешения данные для обучения и тестирования представляли собой комбинацию данных, генерируемых компьютером, и экспериментальных данных. Компьютерные данные дают четкий доступ к истине, тогда как экспериментальные данные содержат неописуемые предубеждения, которые могут повлиять на процесс вывода.

Здесь мы предлагаем организовать международную открытую совместную задачу по количественной оценке и анализу движений молекул в живых клетках с помощью SPT и FCS. На сегодняшний день получение реалистичных данных, смоделированных на компьютере, затруднено из-за количества экспериментальных отклонений, которые необходимо учитывать, и из-за разнообразия моделей диффузии, в частности, для аномальной диффузии.Для этой задачи мы сгенерируем данные SPT и FCS из одного и того же набора смоделированных траекторий и в разных модальностях (2D в мембранах и 3D в ядре) с использованием специального программного обеспечения для моделирования с открытым исходным кодом simSPT (https://gitlab.com / tjian-darzacq-lab / simSPT), который бесплатно доступен участникам для создания собственных дополнительных обучающих наборов, если это необходимо.

Задача будет организована вокруг различных подзадач, которые представляют основные классы экспериментальных ситуаций (короткие траектории высокой плотности в мембранах, менее плотные длинные траектории в мембранах, очень короткие траектории в ядре) и основные типы броуновских и аномальных диффузия (броуновское движение, дробное броуновское движение, случайные блуждания в непрерывном времени и диффузия на фракталах) и их смеси.В долгосрочной перспективе мы также предложим дополнительные задачи, в которых динамика молекулы зависит от местоположения, чтобы имитировать локализованную пространственную неоднородность в динамике (локальные потенциалы, зависящие от положения коэффициенты диффузии). Более того, мы будем постепенно предлагать две категории задач. В задачах вывода параметров будут представлены модели, используемые для генерации траекторий (броуновское движение, аномальная диффузия,…), и задача будет заключаться в том, чтобы как можно точнее вывести значение параметров, используемых для генерации. В задачах выбора модели цель будет заключаться в том, чтобы сделать вывод, какая модель использовалась для генерации данных с учетом известного ограниченного списка моделей.

Наконец, мы понимаем, что вполне возможно, что ни один универсальный инструмент не сможет решить все подзадачи, упомянутые выше. Мы также понимаем, что сложность каждой подзадачи может быть весьма различной. Поэтому мы предлагаем начать с простых задач и работать в сотрудничестве с сообществом, занимающимся анализом молекулярной динамики в живых клетках, чтобы постепенно подниматься по ступеням к более сложным подзадачам.В этой стратегии первостепенное значение имеет поддержание открытого канала связи между организаторами и участниками. С этой целью мы предлагаем начать со списка рассылки, который будет использоваться для поддержки этого общения. Поэтому каждый заинтересованный человек может подписаться на список рассылки проблемы, посетив https://listes.services.cnrs.fr/wws/info/diffusion.challenge. После регистрации в списке рассылки через этот веб-сайт участники смогут обмениваться сообщениями с собой и с организаторами, и они получат инструкции для доступа к наборам данных конкурса.

Авторские взносы

MW, II, CF и HB разработали эти перспективы и написали рукопись.

Финансирование

Эта работа частично финансировалась GDR ImaBio, поддерживаемой CNRS, http://imabio-cnrs.fr.

Конфликт интересов

Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.

Список литературы

1.Аксельрод Д., Коппель Д.Е., Шлессингер Дж., Элсон Э., Уэбб WW. Измерение подвижности путем анализа кинетики восстановления флуоресцентного фотообесцвечивания. Biophys J . (1976) 16 : 1055–69. DOI: 10.1016 / S0006-3495 (76) 85755-4

PubMed Аннотация | CrossRef Полный текст | Google Scholar

2. Магде Д., Уэбб В., Элсон Э. Термодинамические флуктуации в реагирующей системе – измерение с помощью флуоресцентной корреляционной спектроскопии. Phys Rev Lett . (1972) 29 : 705.DOI: 10.1103 / PhysRevLett.29.705

CrossRef Полный текст | Google Scholar

3. Гертс Х., Де Брабандер М., Нюйденс Р., Гойенс С., Моэреманс М., Де Мей Дж. И др. Трекинг нановидов: новый автоматический метод исследования подвижности живых клеток на основе коллоидного золота и видеомикроскопии. Biophys J . (1987) 52 : 775–82. DOI: 10.1016 / S0006-3495 (87) 83271-X

PubMed Аннотация | CrossRef Полный текст | Google Scholar

5. Хейм Р., Прашер округ Колумбия, Цзянь Р. Я.Мутации длины волны и посттрансляционное автоокисление зеленого флуоресцентного белка. Proc Natl Acad Sci USA . (1994) 91 : 12501–4. DOI: 10.1073 / pnas.91.26.12501

PubMed Аннотация | CrossRef Полный текст | Google Scholar

6. Хейм Р., Цзянь Р. Я. Разработка зеленого флуоресцентного белка для повышения яркости, увеличения длины волны и резонансной передачи энергии флуоресценции. Курр Биол . (1996) 6 : 178–82. DOI: 10.1016 / S0960-9822 (02) 00450-5

PubMed Аннотация | CrossRef Полный текст | Google Scholar

7.Мац М.В., Фрадков А.Ф., Лабас Ю.А., Савицкий А.П., Зарайский А.Г., Маркелов М.Л. и др. Флуоресцентные белки небиолюминесцентных видов Anthozoa. Нат Биотехнология . (1999) 17 : 969–73. DOI: 10.1038 / 13657

PubMed Аннотация | CrossRef Полный текст | Google Scholar

8. Hell SW, Wichmann J. Нарушение предела дифракционного разрешения с помощью стимулированного излучения: флуоресцентная микроскопия с истощением стимулированного излучения. Opt Lett . (1994) 19 : 780–2.DOI: 10.1364 / OL.19.000780

PubMed Аннотация | CrossRef Полный текст | Google Scholar

9. Бетциг Э. , Паттерсон Г. Х., Суграт Р., Линдвассер О. В., Оленич С., Бонифачино Дж. С. и др. Визуализация внутриклеточных флуоресцентных белков с нанометровым разрешением. Наука . (2006) 313 : 1642–5. DOI: 10.1126 / science.1127344

PubMed Аннотация | CrossRef Полный текст | Google Scholar

10. Hess ST, Girirajan TP, Mason MD. Получение изображений сверхвысокого разрешения с помощью микроскопии локализации флуоресцентной фотоактивации. Biophys J . (2006) 91 : 02222. DOI: 10.1529 / biophysj.106.0

PubMed Аннотация | CrossRef Полный текст | Google Scholar

11. Клар Т.А., Якобс С., Дыба М., Эгнер А., Hell SW. Флуоресцентная микроскопия с дифракционным барьером разрешения, нарушенным вынужденным излучением. Proc Natl Acad Sci USA . (2000) 97 : 8206–10. DOI: 10.1073 / pnas.97.15.8206

PubMed Аннотация | CrossRef Полный текст | Google Scholar

13.Manley S, Gillette JM, Patterson GH, Shroff H, Hess HF, Betzig E, et al. Картирование траекторий одиночных молекул с высокой плотностью при помощи фотоактивированной локализационной микроскопии. Нат Методы . (2008) 5 : 155–7. DOI: 10.1038 / nmeth.1176

PubMed Аннотация | CrossRef Полный текст | Google Scholar

14. Эггелинг К., Рингеманн С., Медда Р., Шварцманн Г., Сандхофф К., Полякова С. и др. Прямое наблюдение за наноразмерной динамикой мембранных липидов в живой клетке. Природа . (2009) 457 : 1159–62. DOI: 10.1038 / nature07596

PubMed Аннотация | CrossRef Полный текст | Google Scholar

15. Саркар П., Чаттопадхай А. Изучение организации мембран при различных пространственно-временных разрешениях с использованием подходов, основанных на флуоресценции: значение для мембранной биологии. Phys Chem Chem Phys . (2019) 21 : 11554–63. DOI: 10.1039 / C9CP02087J

PubMed Аннотация | CrossRef Полный текст | Google Scholar

17. Прист Д.Г., Солано А., Лу Дж., Хинд Э. Флуоресцентная флуоресцентная спектроскопия: бесценный инструмент микроскопии для раскрытия биофизических правил навигации по ядерному ландшафту. Biochem Soc Trans . (2019) 47 : 1117–29. DOI: 10.1042 / BST20180604

PubMed Аннотация | CrossRef Полный текст | Google Scholar

19. Etoc F, Balloul E, Vicario C, Normanno D, Lie D, Sittner A, et al. Неспецифические взаимодействия регулируют цитозольную диффузию наноразмерных объектов в клетках млекопитающих. Нат Матер . (2018) 17 : 740–6. DOI: 10.1038 / s41563-018-0120-7

PubMed Аннотация | CrossRef Полный текст | Google Scholar

20. Вейгель А.В., Саймон Б., Тамкун М.М., Крапф Д. Эргодические и неэргодические процессы сосуществуют в плазматической мембране, что наблюдается при отслеживании одиночных молекул. Proc Natl Acad Sci USA . (2011) 108 : 6438–43. DOI: 10.1073 / pnas.1016325108

PubMed Аннотация | CrossRef Полный текст | Google Scholar

21.Эрнст Д., Хеллманн М., Кёлер Дж., Вайс М. Дробное броуновское движение в переполненных жидкостях. Мягкое вещество . (2012) 8 : 4886–9. DOI: 10.1039 / c2sm25220a

CrossRef Полный текст | Google Scholar

23. Burnecki K, Kepten E, Janczura J, Bronshtein I., Garini Y, Weron A. Универсальный алгоритм для идентификации дробного броуновского движения. Случай субдиффузии теломер. Biophys J . (2012) 103 : 1839–47. DOI: 10.1016 / j.bpj.2012.09.040

PubMed Аннотация | CrossRef Полный текст | Google Scholar

24.Rcamier V, Izeddin I, Bosanac L, Dahan M, Proux F, Darzacq X. Одноклеточная корреляционная фрактальная размерность хроматина: основа для интерпретации трехмерного сверхразрешения одиночных молекул. Ядро . (2014) 5 : 75–84. DOI: 10.4161 / nucl.28227

PubMed Аннотация | CrossRef Полный текст | Google Scholar

25. Шабани М.Р., Ригер Х. Переходная аномальная диффузия в динамике бега-натыкания. Передняя Физика . (2019) 7 : 120. DOI: 10.3389 / fphy.2019.00120

CrossRef Полный текст | Google Scholar

27. Ревери JF, Jeon JH, Bao H, Leippe M, Metzler R, Selhuber-Unkel C. Супердиффузия доминирует внутриклеточное движение частиц в переполненной цитоплазме патогенной Acanthamoeba castellanii . Научная репутация . (2015) 5 : 11690. DOI: 10.1038 / srep11690

PubMed Аннотация | CrossRef Полный текст | Google Scholar

28. Бруно Л., Леви В., Брунштейн М., Деспозито М.А. Переход к супердиффузионному поведению во внутриклеточном транспорте актина, опосредованном молекулярными моторами. Phys Rev E . (2009) 80 : 011912. DOI: 10.1103 / PhysRevE.80.011912

PubMed Аннотация | CrossRef Полный текст | Google Scholar

30. Метцлер Р., Чон Дж. Х., Черствый А.Г., Баркай Э. Модели аномальной диффузии и их свойства: нестационарность, неэргодичность и старение к столетию отслеживания одиночных частиц. Phys Chem Chem Phys . (2014) 16 : 24128–64. DOI: 10.1039 / C4CP03465A

PubMed Аннотация | CrossRef Полный текст | Google Scholar

31.Павлос Г.П., Каракацанис Л.П., Ксенакис М.Н., Павлос Э.Г., Илиопулос А.С., Сарафопулос Д.В. Универсальность неэквивалентной статистики Цаллиса и анализа временных рядов: теория и приложения. Phys A Stat Mech Appl . (2014) 395 : 58–95. DOI: 10.1016 / j.physa.2013.08.026

CrossRef Полный текст | Google Scholar

32. Лензи Е.К., Рибейро Х.В., Татейши А.А., Зола Р.С., Евангелиста Л.Р. Аномальная диффузия и перенос в гетерогенных системах, разделенных мембраной. Proc R Soc A Math Phys Eng Sci .(2016) 472 : 20160502. DOI: 10.1098 / rspa.2016.0502

PubMed Аннотация | CrossRef Полный текст | Google Scholar

33. Wawrezinieck L, Rigneault H, Marguet D, Lenne PF. Законы диффузии флуоресцентной корреляционной спектроскопии для исследования субмикронной организации клеточной мембраны. Biophys J . (2005) 89 : 4029–42. DOI: 10.1529 / biophysj.105.067959

PubMed Аннотация | CrossRef Полный текст | Google Scholar

34. Петрек З., Швилле П.Точное измерение коэффициентов диффузии с помощью сканирующей флуоресцентной корреляционной спектроскопии. Biophys J . (2008) 94 : 1437–48. DOI: 10.1529 / biophysj.107.108811

PubMed Аннотация | CrossRef Полный текст | Google Scholar

35. Хонигманн А., Мюллер В., Та Х., Шенле А., Сезгин Е., Хелл С.В. и др. Сканирование STED-FCS выявляет пространственно-временную неоднородность липидного взаимодействия в плазматической мембране живых клеток. Нац Коммуна . (2014) 5 : 5412.DOI: 10.1038 / ncomms6412

PubMed Аннотация | CrossRef Полный текст | Google Scholar

36. Дигман М.А., Браун С.М., Сенгупта П., Вайзман П.В., Хорвиц А.Р., Граттон Э. Измерение быстрой динамики в растворах и клетках с помощью лазерного сканирующего микроскопа. Biophys J . (2005) 89 : 1317–27. DOI: 10.1529 / biophysj.105.062836

PubMed Аннотация | CrossRef Полный текст | Google Scholar

37. Каннан Б., Хар Дж. Й., Лю П., Маруяма И., Динг Дж. Л., Уоланд Т. Электронно-умножающее устройство с зарядовой связью на основе флуоресцентной корреляционной спектроскопии на основе камеры. Анальный Химик . (2006) 78 : 3444–51. DOI: 10.1021 / ac0600959

PubMed Аннотация | CrossRef Полный текст | Google Scholar

40. Гуо С.М., Хе Дж., Монье Н., Сан Дж., Воланд Т., Бат М. Байесовский подход к анализу данных флуоресцентной корреляционной спектроскопии II: применение к смоделированным данным и данным in vitro . Анальный Химик . (2012) 84 : 3880–8. DOI: 10.1021 / ac2034375

PubMed Аннотация | CrossRef Полный текст | Google Scholar

41.Lenne PF, Wawrezinieck L, Conchonaud F, Wurtz O, Boned A, Guo XJ и др. Динамическое ограничение молекул в плазматической мембране микродоменами и сеткой цитоскелета. EMBO J . (2006) 25 : 3245–56. DOI: 10.1038 / sj.emboj.7601214

PubMed Аннотация | CrossRef Полный текст | Google Scholar

42. Favard C, Wenger J, Lenne PF, Rigneault H. Законы диффузии FCS в двухфазных липидных мембранах: определение среднего размера домена с помощью экспериментов и моделирования Монте-Карло. Biophys J . (2011) 100 : 1242–51. DOI: 10.1016 / j.bpj.2010.12.3738

PubMed Аннотация | CrossRef Полный текст | Google Scholar

43. Бэнкс Д.С., Тресслер С., Петерс Р.Д., Хфлинг Ф., Фрадин С. Характеристика аномальной диффузии в плотных полимерных растворах и гелях в течение пяти десятилетий во времени с помощью флуоресцентной корреляционной спектроскопии с переменным масштабом длины. Мягкое вещество . (2016) 12 : 4190–203. DOI: 10.1039 / C5SM01213A

PubMed Аннотация | CrossRef Полный текст | Google Scholar

44.Масуда А., Ушида К., Окамото Т. Прямое наблюдение пространственно-временной зависимости аномальной диффузии в неоднородной жидкости с помощью флуоресцентной корреляционной спектроскопии с контролем объема проб. Phys Rev E . (2005) 72 : 060101. DOI: 10.1103 / PhysRevE.72.060101

PubMed Аннотация | CrossRef Полный текст | Google Scholar

45. Шнайдер Ф., Вайте Д., Галиани С., Бернардино де ла Серна Дж., Сезгин Э., Эггелинг С. Наноуровневые пространственно-временные режимы диффузии, измеренные с помощью одновременной конфокальной и индуцированной наноскопии истощения излучения. Nano Lett . (2018) 18 : 4233–40. DOI: 10.1021 / acs.nanolett.8b01190

PubMed Аннотация | CrossRef Полный текст | Google Scholar

48. Изеддин I, Рекамье V, Босанак Л., Сиссе II, Бударен Л., Дугаст-Дарзак К. и др. Отслеживание одиночных молекул в живых клетках выявляет различные стратегии поиска мишеней факторов транскрипции в ядре. eLife . (2014) 3 : e02230. DOI: 10.7554 / eLife.02230

PubMed Аннотация | CrossRef Полный текст | Google Scholar

51.Флоренс-Змироу Д. Об оценке коэффициента диффузии по дискретным наблюдениям. J Приложение Probab . (1993) 30 : 790. DOI: 10.1017 / S0021

0044570

CrossRef Полный текст | Google Scholar

52. Хоффманн М. Об оценке коэффициента диффузии: параметрический и непараметрический. Ann l’IHP Probab Stat . (2001) 37 : 339–72. DOI: 10.1016 / S0246-0203 (00) 01070-0

CrossRef Полный текст | Google Scholar

53.Цянь Х., Шитц М.П., Элсон Э.Л. Отслеживание одиночных частиц. Анализ диффузии и течения в двумерных системах. Biophys J . (1991) 60 : 910–21. DOI: 10.1016 / S0006-3495 (91) 82125-7

PubMed Аннотация | CrossRef Полный текст | Google Scholar

56. Михале X. Анализ среднеквадратичного смещения траекторий одиночных частиц с ошибкой локализации: броуновское движение в изотропной среде. Phys Rev E . (2010) 82 : 041914. DOI: 10.1103 / PhysRevE.82.041914

PubMed Аннотация | CrossRef Полный текст | Google Scholar

57. Бойер Д., Дин Д.С., Мехиа-Монастерио С., Ошанин Г. Оптимальные оценки коэффициента диффузии одной броуновской траектории. Phys Rev E . (2012) 85 : 031136. DOI: 10.1103 / PhysRevE.85.031136

PubMed Аннотация | CrossRef Полный текст | Google Scholar

58. Хансен А.С., Ворингер М., Гримм Дж. Б., Лавис Л.Д., Тьян Р., Дарзак Х. Надежный модельный анализ экспериментов по отслеживанию одиночных частиц с пятном. eLife . (2018) 7 : e33125. DOI: 10.7554 / eLife.33125

PubMed Аннотация | CrossRef Полный текст | Google Scholar

59. Monnier N, Guo SM, Mori M, He J, Lénárt P, Bathe M. Байесовский подход к основанному на MSD анализу движения частиц в живых клетках. Biophys J . (2012) 103 : 616–26. DOI: 10.1016 / j.bpj.2012.06.029

PubMed Аннотация | CrossRef Полный текст | Google Scholar

60. Monnier N, Barry Z, Park HY, Su KC, Katz Z, English BP, et al.Выявление транзиторной динамики переноса частиц в живых клетках. Нат Методы . (2015) 12 : 838–40. DOI: 10.1038 / nmeth.3483

PubMed Аннотация | CrossRef Полный текст | Google Scholar

61. Slator PJ, Каир CW, Берроуз, штат Нью-Джерси. Обнаружение диффузионной неоднородности в траекториях слежения за одиночными частицами с использованием скрытой марковской модели с измерением распространения шума. PLOS ONE . (2015) 10 : e0140759. DOI: 10.1371 / journal.pone.0140759

PubMed Аннотация | CrossRef Полный текст | Google Scholar

63.Blei DM, Kucukelbir A, McAuliffe JD. Вариационный вывод: обзор для статистиков. arXiv . (2016) 112 : 859–77. DOI: 10.1080 / 01621459.2017.1285773

CrossRef Полный текст | Google Scholar

64. Перссон Ф., Линдн М., Юносон С., Эльф Дж. Извлечение внутриклеточных диффузионных состояний и скоростей переходов из данных отслеживания одиночных молекул. Нат Методы . (2013) 10 : 265–9. DOI: 10.1038 / nmeth.2367

PubMed Аннотация | CrossRef Полный текст | Google Scholar

66.Masson JB, Casanova D, Türkcan S, Voisinne G, Popoff MR, Vergassola M и др. Составление карт сил внутри микродоменов клеточной мембраны. Phys Rev Lett . (2009) 102 : 048103. DOI: 10.1103 / PhysRevLett.102.048103

PubMed Аннотация | CrossRef Полный текст | Google Scholar

68. Флодерер К., Массон Дж. Б., Бойли Е., Джорджо С., Мерида П., Эль Бехейри М. и др. Микроскопия локализации одной молекулы показывает, как Gag-белки ВИЧ-1 воспринимают мембранные сайты сборки вируса в живых CD4 Т-клетках хозяина. Научная репутация . (2018) 8 : 16283. DOI: 10.1038 / s41598-018-34536-y

PubMed Аннотация | CrossRef Полный текст | Google Scholar

70. Шкилев В.П. Кинетическая модель для экспериментов флуоресцентной микроскопии в неупорядоченных средах, содержащих сайты связывания и препятствия. Phys Rev E . (2018) 98 : 032140. DOI: 10.1103 / PhysRevE.98.032140

CrossRef Полный текст | Google Scholar

71. Крог Дж., Якобсен Л. Х., Лунд Ф. В., Встнер Д., Ломхольт Массачусетс.Выбор байесовской модели с дробным броуновским движением. J Stat Mech Theory Exp . (2018) 2018 : 093501. DOI: 10.1088 / 1742-5468 / aadb0e

CrossRef Полный текст | Google Scholar

72. Бойер Д., Дин Д.С., Мехиа-Монастерио С., Ошанин Г. Об эргодических оценках методом наименьших квадратов обобщенного коэффициента диффузии для дробного броуновского движения. Biophys J . (2013) 87 : 030103. DOI: 10.1103 / PhysRevE.87.030103

CrossRef Полный текст | Google Scholar

73.Робсон А., Беррейдж К., Лик М.С. Делая вывод о диффузии в отдельных живых клетках на уровне одной молекулы. Philos Trans R Soc B Biol Sci . (2012) 368 : 20120029. DOI: 10.1098 / rstb.2012.0029

PubMed Аннотация | CrossRef Полный текст | Google Scholar

74. Hellmann M, Klafter J, Heermann DW, Weiss M. Проблемы определения аномальной диффузии в переполненных флюидах. Дж. Phys Condens Matter . (2011) 23 : 234113. DOI: 10.1088 / 0953-8984 / 23/23/234113

PubMed Аннотация | CrossRef Полный текст | Google Scholar

75.Магдиарц М., Верон А., Бурнеки К., Клафтер Дж. Дробное броуновское движение в сравнении со случайным блужданием в непрерывном времени: простой тест на субдиффузионную динамику. Phys Rev Lett . (2009) 103 : 180602. DOI: 10.1103 / PhysRevLett.103.180602

PubMed Аннотация | CrossRef Полный текст | Google Scholar

77. Кондамин С., Техедор В., Войтуриес Р., Бенишоу О., Клафтер Дж. Исследование микроскопического происхождения ограниченной субдиффузии с помощью наблюдений первого прохода. Proc Natl Acad Sci USA .(2008) 105 : 5675–80. DOI: 10.1073 / pnas.0712158105

PubMed Аннотация | CrossRef Полный текст | Google Scholar

78. Thapa S, Lomholt MA, Krog J, Cherstvy AG, Metzler R. Байесовский анализ данных слежения за отдельными частицами с использованием алгоритма вложенной выборки: выбор модели максимального правдоподобия применяется к данным стохастической диффузии. Phys Chem Chem Phys . (2018) 20 : 29018–37. DOI: 10.1039 / C8CP04043E

PubMed Аннотация | CrossRef Полный текст | Google Scholar

79.Вебер С.К., Томпсон М.А., Моернер В.Е., Спаковиц А.Дж., Териот Дж.А. Аналитические инструменты, позволяющие различать влияние ошибки локализации, ограничения и упругости среды на функцию автокорреляции скорости. Biophys J . (2012) 102 : 2443–50. DOI: 10.1016 / j.bpj.2012.03.062

PubMed Аннотация | CrossRef Полный текст | Google Scholar

80. Вестергаард К.Л., Блейни П.С., Фливбьерг Х. Оптимальная оценка коэффициентов диффузии по траекториям одиночных частиц. Phys Rev E . (2014) 89 : 022726. DOI: 10.1103 / PhysRevE.89.022726

PubMed Аннотация | CrossRef Полный текст | Google Scholar

82. Хансен А.С., Амитаи А., Каттольо С., Тьянь Р., Дарзакк X. Управляемая ядерная разведка повышает эффективность поиска целей CTCF. bioRXiv . (2018) 495457. DOI: 10.1101 / 495457

PubMed Аннотация | CrossRef Полный текст

83. Türkcan S, Alexandrou A, Masson JB. Схема байесовского вывода для извлечения коэффициента диффузии и потенциальных полей из ограниченных траекторий одиночных молекул. Biophys J . (2012) 102 : 2288–98. DOI: 10.1016 / j.bpj.2012.01.063

PubMed Аннотация | CrossRef Полный текст | Google Scholar

84. Массон Дж. Б., Дионн П., Сальватико К., Реннер М., Шпехт К. Г., Триллер А. и др. Картирование энергетических и диффузионных ландшафтов мембранных белков на поверхности клетки с использованием высокоплотной визуализации одиночных молекул и байесовского вывода: приложение к многомасштабной динамике рецепторов глицина в нейрональной мембране. Biophys J .(2014) 106 : 74–83. DOI: 10.1016 / j.bpj.2013.10.027

PubMed Аннотация | CrossRef Полный текст | Google Scholar

86. Chenouard N, Smal I., de Chaumont F, Maka M, Sbalzarini IF, Gong Y, et al. Объективное сравнение методов отслеживания частиц. Нат Методы . (2014) 11 : 281–9. DOI: 10.1038 / Nmeth.2808

PubMed Аннотация | CrossRef Полный текст | Google Scholar

87. Сейдж Д., Фам Та, Бэбкок Х., Лукес Т., Пенго Т., Чао Дж. И др.Бойцовский клуб сверхвысокого разрешения: оценка программного обеспечения для 2D и 3D микроскопии локализации одиночных молекул. Нат Методы . (2019) 16 : 387–95. DOI: 10.1101 / 362517

PubMed Аннотация | CrossRef Полный текст | Google Scholar

88. Муньос-Хиль Дж., Вольпе Дж., Гарсия-Марч М.А., Мецлер Р., Левенштейн М., Манзо К. Анди: проблема аномальной диффузии. arXiv. (2020) ArXiv: 2003.12036 .

Google Scholar

(PDF) Супердиффузионное движение нацеленных на мембрану доменов C2

www.nature.com/scientificreports/

НАУЧНЫЕ ОТЧЕТЫ | 5: 17721 | DOI: 10.1038 / srep17721

температура в течение 30 минут, затем поместили при 4 ° C на ночь. Образцы диализовали против 1 л 50 мМ

HEPES, pH 7,0, 75 мМ NaCl, 4 мМ MgCl

и 5% глицерина в течение ночи при 4 ° C, затем концентрировали до 10 мкМ.

Imaging. Белки добавляли в буфер для визуализации до конечной концентрации 75 пМ. Затем камера слияния per

была заполнена раствором, и после короткого периода инкубации в 10 минут мы начали формирование изображений

.Используемые перфузионные камеры имели диаметр 9 мм и глубину 0,9 мм, вмещая объем

≈ 60 мкл. Визуализацию проводили без замены раствора, так что всегда было давление белка в основной массе раствора, а концентрация на поверхности могла достигать устойчивого состояния.

Все изображения были получены с использованием люминесцентного микроскопа полного внутреннего отражения объективного типа

(TIRFM). Микроскоп был построен на основе корпуса Olympus IX71

18,36

с лазерной линией 561 нм

в качестве источника возбуждения.Использовалась камера

(Andor iXon DU-888) устройства электронного умножения с зарядовой связью (EMCCD) с задней подсветкой, жидкостное охлаждение до -85 ° C, с электронным усилением 300. Чтобы

поддерживать постоянную фокусировку в течение всего времени визуализации, мы использовали систему автофокусировки (CRISP,

Applied Scientic Instrumentation, Евгений, Орегон) в сочетании с пьезоэлектрическим столиком (Z-100, Mad

City Labs, Мэдисон, Висконсин). Видео были получены с частотой кадров 20 кадров / с.

Обработка изображений и отслеживание отдельных частиц. Изображения были получены с использованием программного обеспечения Andor IQ 2.3

и сохранены в виде 16-битных файлов. Затем изображения были отфильтрованы с использованием ядра Гаусса со стандартным отклонением

на 1,0 пиксель в ImageJ. Одночастичное отслеживание Atto-C2 и Atto-GST-C2 было выполнено в

MATLAB с использованием алгоритма U-track, разработанного Jaqaman et al.

при тщательной ручной проверке

обнаружения и отслеживания.

Ссылки

1. Херли, Дж. Х. Мембранные связывающие домены. Биохим. Биофиз. Acta 1761, 805–811 (2006).

2. Леммон, М. А. Распознавание мембраны фосфолипид-связывающими доменами. Nat. Ev. Мол. Cell Biol. 9. С. 99–111 (2008).

3. Леммон М. и Фергюсон Э. Сигнал-зависимое нацеливание на мембрану доменами гомологии плекестрина (PH). Биохим. J. 350,

1–18 (2000).

4. Cho, W. & Stahelin,. V. Связывание с мембраной и субклеточное нацеливание доменов C2.Биохим. Биофиз. Acta 1761, 838–849 (2006).

5. Letunic, I., Doers, T. & Bor, P. SMAT 7: последние обновления ресурса аннотации белкового домена. Нуклеиновые кислоты es. 40,

D302 – D305 (2012). http://smart.embl-heidelberg.de/.

6. Найт, Дж. Д. и Фалке, Дж. Дж. Исследования флуоресценции одиночных молекул домена PH: новые взгляды на мембрану, регистрирующую реакцию

. Биофиз. J. 96, 566–582 (2009).

7. Ясуи, М., Мацуога, С. и Уэда, М.Прыжки PTEN на клеточной мембране регулируются положительно заряженным доменом C2. PLoS

Вычисл. Биол. 10, e1003817 (2014).

8. Gerice, A., Munson, M. & oss, A.H. Регулирование фосфатазы PTEN. Gene 374, 1–9 (2006).

9. Дас, С., Диксон, Дж. Э. и Чо, В. Механизм связывания с мембраной и активации PTEN. Proc. Natl. Акад. Sci. США. 100,

7491–7496 (2003).

10. Barai, E., Garini, Y. & Metzler,. Странная кинетика одиночных молекул в живых клетках.Phys. Сегодня 65, 29–35 (2012).

11. Höing, F. & Franosch, T. Аномальный транспорт в переполненном мире биологических клеток. Ep. Прог. Phys. 76, 046602 (2013).

12. Метцлер Э., Чон Дж.-Х., Черствы А.Г., Баркаи Э. Модели аномальной диффузии и их свойства: нестационарность, не-

эргодичность и старение 100-летие отслеживания одиночных частиц. Phys. Chem. Chem. Phys. 16. С. 24128–24164 (2014).

13. rapf, D. Механизмы, лежащие в основе аномальной диффузии в плазматической мембране.Curr. Верхний. Membr. 75, 167–207 (2015).

14. Голдинг И. и Кокс Э. С. Физическая природа цитоплазмы бактерий. Phys. Ev. Lett. 96, 098102 (2006).

15. Толич-Норрелиже, И. М., Мунтяну, Э.-Л., Эон, Г., Оддершеде, Л., и Берг-Соренсен,. Аномальная диффузия в живых дрожжах

клеток. Phys. Ev. Lett. 93, 078102 (2004).

16. Jeon, J.-H. и другие. In vivo аномальная диффузия и нарушение эргодичности липидных гранул. Phys. Ev. Lett. 106, 048103 (2011).

17. Бронштейн И. и др. Временная аномальная диффузия теломер в ядре клеток млекопитающих. Phys. Ev. Lett. 103, 018102

(2009).

18. Вейгель, А. В., Тамун, М. М. & rapf, Д. Количественная оценка динамических взаимодействий между ямой, покрытой клатрином, и молекулами груза

. Proc. Natl. Акад. Sci. США. 110, E4591 – E4600 (2013).

19. Heinemann, F., Vogel, S.. & Schwille, P. Боковая мембранная диффузия, модулируемая минимальной актиновой корой.Биофиз. J. 104,

1465–1475 (2013).

20. Torreno-Pina, J. A. et al. Усиление взаимодействий рецептор-клатрин, индуцированное N-гликаном-опосредованным мембранным микропроцессором.

Proc. Natl. Акад. Sci. США. 111. С. 11037–11042 (2014).

21. Bans, D. S. & Fradin, C. Аномальная диффузия белков из-за молекулярного скопления. Биофиз. J. 89, 2960–2971 (2005).

22. Szymans J.i, J. & Weiss, M. Выяснение происхождения аномальной диффузии в плотных жидкостях.Phys. Ev. Lett. 103, 038102 (2009).

23. Horton, M.., Höing, F., ädler, J. O. & Franosch, T. Развитие аномальной диффузии среди белков краудинга. S o

Matter 6, 2648–2656 (2010).

24. Jeon, J.-H., Monne, H. M.-S., Javanainen, M. & Metzler,. Аномальная диффузия фосфолипидов и холестеринов в липидный бислой

и его происхождение. Phys. Ev. Lett. 109, 188103 (2012).

25. Bursac, P. et al. Динамика цитоскелетов: «колебания в сети».Биохим. Биофиз. es. Comm. 355. С. 324–330 (2007).

26. Шахана А., Шенан Г., Фейнгольд М., Эльбаум М. и Гране Э. Активный транспорт по неупорядоченным сетям микротрубочек: e

обобщенная модель случайных скоростей. Phys. Ev. Е 78, 051912 (2008).

27. Бруно, Л., Леви, В., Брунштейн, М. и Деспозито, М. Переход к сверхдиагностическому поведению при внутриклеточном транспорте на основе актина

, опосредованном молекулярными моторами. Phys. Ev. Е 80, 011912 (2009).

28.Aimoto, T. Распределительный ответ на предубеждения в детерминированной сверхдиффузии. Phys. Ev. Lett. 108, 164101 (2012).

29. Шлезинджер, М. Ф. и Шладер, Дж. Леви Валес против Леви Райта. В Стэнли, Х. Э. и Островски, Н. (ред.) О росте и форме: фрактал

и нефрактальные паттерны в физике. 279–283 (Springer, 1986).

30. laer, J., Shlesinger, M. F. & Zumofen, G. За пределами броуновского движения. Phys. Сегодня 49, 33–39 (1996).

31. Saug, M. J., Мабри Дж. И Шварц Д. Э. Прерывистые молекулярные прыжки на границе твердое тело-жидкость. Phys. Ev. Lett. 110, 256101

(2013).

32. Yu, C., Guan, J., Chen,., Bae, S.C., Granic, S. Наблюдение длинных скачков адсорбции полимера с помощью одной молекулы. АСУ Нано

7, 9735–9742 (2013).

33. Bouchaud, J.-P. Нарушение эргодичности тела и старение в неупорядоченных системах. J. Physique I 2, 1705–1713 (1992).

Автоматическое определение режимов диффузии в биологических мембранах с помощью нейронной сети обратного распространения | BMC Bioinformatics

A.Архитектура и алгоритм нейронных сетей обратного распространения

BPNN была создана с одним скрытым слоем между модулями ввода и вывода (рис. 1). Все узлы слоя были связаны со всеми узлами соседних слоев. BPNN включала две рабочие фазы: этап обучения и этап отзыва. На этапе обучения известные наборы данных использовались в качестве обучающего сигнала на входном и выходном уровнях. Первой операцией на этапе обучения является операция прямой связи. Во время этой операции каждый входной нейрон получает входной сигнал и передает этот сигнал подключенным нейронам в скрытом слое.m {W} _ {ij} {X} _i} \ right) \ right) $$

(1)

O _к – расчетный выход k ^{-й нейрон} в выходном слое, X _и входные значения сети, Вт _ij вес соединения от узла i (входной уровень) до узла j (скрытый слой), W _jk – вес соединения от узла j (скрытый слой) к узлу k (выходной слой), f – это функция активации нейрона, которая классически является сигмоидной функцией, как определено в уравнении.2} $$

(3)

p – количество выходных нейронов, O _к и T _к – это расчетный выход и целевой выход, соответственно, k ^{-й нейрон} в выходном слое.

Вторая операция фазы обучения – это обратный проход, в котором метод градиентного спуска используется для минимизации ошибки в обучающем наборе. Начиная с выходного уровня, ошибка распространяется в обратном направлении по сети, слой за слоем, путем рекурсивного вычисления локальной градиентной ошибки каждого нейрона. Затем вес соединения изменяется пропорционально отрицательному значению производной ошибки с помощью следующего уравнения:

$$ \ varDelta {W} _ {i, j} \ left (t + 1 \ right) = – \ eta \ frac {\ partial E} {\ partial {W} _ {i, j}} + \ alpha \ varDelta {W} _ {i, j} (t) $$

(4)

ΔW _{и , и} ( t + 1) – приращение веса, минимизирующее E между j ^{-й нейрон} и -й ^{-й нейрон} на (t + 1) ^{-й итерации}. η – скорость обучения, а α – параметр импульса. α выбирается между 0 и 1, обычно 0,9, значение, обеспечивающее высокую скорость обучения [24]. Использование импульсного члена – это самый простой способ избежать проблем с колебаниями при поиске минимального значения поверхности ошибки. Этот процесс вперед-назад повторяется для каждого входного сигнала.

BPNN обучается путем многократного представления серии наборов шаблонов ввода / вывода для минимизации среднеквадратичной ошибки (MSE) (уравнение. 2} \ right \}} $$

(6)

, где δt – временной интервал между двумя последовательными кадрами, x (t) и y (t) – координаты частицы в момент времени t , N – общее количество кадров, а n – количество временных интервалов [25] (подробнее см. Раздел «Методы»).Для броуновского движения кривая MSD линейно увеличивается с шагом времени δt . Кривая имеет изгиб вверх или вниз для направленных или ограниченных движений соответственно. В нашей системе 3 типа движений, описанных выше, различаются путем анализа траектории с помощью алгоритма с использованием скользящего окна размером S1 (рис. 1b). Была построена трехслойная BPNN с тремя выходными узлами, по одному для каждого типа движения, а именно броуновского, направленного и ограниченного.Мы выбрали один скрытый слой с пятью скрытыми узлами (подробнее см. В разделе «Материалы и методы»). Входные переменные были нормализованы и преобразованы в значения в диапазоне 0,0–1,0). Каждому режиму движения присваиваются и нормализуются три выходных значения.

Процедура обучения и наборы проверки

Сеть была обучена с использованием наборов данных смоделированных траекторий. Тысяча траекторий продолжительностью 3,1 с (31 кадр, размер скользящего окна в этом примере) были смоделированы для каждого типа диффузионного режима с шагом времени 100 мс.Для ограниченной диффузии частица демонстрирует броуновскую диффузию в ограниченной области с переменным диаметром L . Для направленной диффузии к броуновскому движению добавляется член постоянной скорости дрейфа V в одном направлении по всей траектории. Одна часть наборов данных используется для обучения, другая – для перекрестной проверки с разными параметрами (см. Материалы и методы).

Производительность обученной BPNN была сначала оценена с использованием новых наивных смоделированных шаблонов и путем вычисления процентной ошибки между рассчитанными выходными и ожидаемыми значениями (вероятность обнаружения).Он увеличивается для данного коэффициента диффузии, когда размер удержания уменьшается для ограниченных траекторий (рис. 2a) или когда скорость увеличивается для направленных траекторий (рис. 2b). Процедура обучения проводилась с 3 различными наборами данных траекторий длительностью 2,1, 3,1 и 4,1 с. В наших условиях аналогичная вероятность обнаружения направленных диффузионных мод была получена для 31 и 41 кадра. Таким образом, размер скользящего окна был зафиксирован на 31 кадре (синяя кривая на рис.2), значение, при котором вероятность обнаружения ограничения диаметром 1 мкм (разумный размер ограничения в клеточных мембранах) все еще возможна и, очевидно, позволяет обнаруживать меньшие сегменты по сравнению с 41 кадром. Учитывая 2 направленные траектории T ₀ и T ₁ с соответствующим коэффициентом диффузии D ₀ и D ₁ и скорость В ₀ и В ₁, нормализованные кривые МСД будут аналогичными, если:

Рис.2

Процент обнаружения ограниченных и направленных режимов диффузии в зависимости от размера скользящего окна S1. Вероятность обнаружения ограничения или направленного движения на смоделированных траекториях была рассчитана для различной длины сегмента, используемого для расчета MSD (S1 равно 21 (красный), 31 (синий) или 41 (зеленый) кадр). Вероятность обнаружения удержания на траекториях выражается как функция удержания диаметра L ( a ), тогда как вероятность обнаружения направленного движения выражается как функция скорости ( b )

$$ {V} _1 = {V} _0 \ sqrt {\ frac {D_1} {D_0}} $$

(7)

Точно так же нормализованные кривые MSD будут подобны для двух ограниченных траекторий T ₀ и T ₁ с соответствующим коэффициентом диффузии D ₀ и D ₁ и ограничивающий диаметр L ₀ и L ₁, если:

$$ {L} _1 = {L} _0 \ sqrt {\ frac {D_1} {D_0}} $$

(8)

Определение порога обнаружения ограниченного и направленного движения в пределах траектории

Описанное выше скользящее окно из 31 кадра используется для разделения траектории на разные сегменты и располагается в точке i = (S ₁ -1) / 2 траектории, чтобы определить первый сегмент, содержащий первые 31 точку.Кривая MSD рассчитывается для этой траектории из 31 кадра и представляется в качестве входных данных для нейронной сети после нормализации. 3 выходных значения нейронной сети O _В, O _С и O _D соответствуют вероятности диффузии частицы в соответствии с одним из трех режимов диффузии (броуновской, ограниченной и направленной соответственно).Эти 3 значения присваиваются каждой раме раздвижных окон. Затем скользящее окно переводится в точку i + 1 , чтобы проанализировать следующий сегмент траектории, и процедура повторяется до точки i + n = N – [(S ₁ -1) / 2] . Для каждого кадра траектории среднее из выходных значений ( O _В , О _С и O _D), соответствующие вероятности назначения одного из 3 режимов распространения каждого кадра во время анализа BPNN, наносятся на график как функция времени (несколько выходных значений предоставляются для данного кадра из-за скользящих окон).Однако статистически некоторые чисто броуновские траектории могут временно демонстрировать поведение, подобное ограниченным или направленным. Поэтому мы определили пороговое значение, чтобы отличить истинную ограниченную или направленную часть траектории от той, что вызвана броуновскими флуктуациями. Для этого было сгенерировано 100 броуновских траекторий из 1000 кадров (приращение времени 100 мс; D, 0,25 мкм ² / с) и проанализировано. Затем мы построили график пороговых значений выходных значений BPNN Y _C (или Y _D) как функцию количества последовательных кадров (от 5 до 45 кадров), для которых процент ошибочно отнесенных к ограниченным (или направленным) сегментам нейросеть не превышала 5% от общего количества кадров броуновской траектории (достоверность 95%) (рис.3). Эти пороговые значения используются для идентификации сегментов, которые ограничены или направлены в пределах траектории (см. Пример на рис. 4c).

Рис. 3

Определение порога обнаружения ограниченных и направленных мод диффузии. Пороги вывода BPNN для режима ограниченной диффузии Y _С (пустые кружки) и мода направленной диффузии Y _D (пустые квадраты) были рассчитаны для ограниченной диффузии ( Y _С) (пустые кружки) и режим направленной диффузии (пустые квадраты) путем построения графика как функции количества последовательных кадров (длины обнаруженного сегмента) выхода BPNN, для которого нейронная сеть неверно указала, в 5% случаев , ограниченное или направленное движение для броуновской траектории

Фиг.4

Анализ режимов движения по синтетическим траекториям. a Вероятность обнаружения с использованием BPNN. 200 траекторий из 400 кадров, включая один сегмент направленного движения со скоростью 1,2 мкм / с и один сегмент ограничения диаметром 1 мкм, были проанализированы с помощью BPPN (ограничены светло-серым, направленным темно-серым цветом; D = 0,25 мкм ² / с , время интегрирования = 100 мс; каждый сегмент из 50 кадров всегда локализован в одной и той же позиции). Процент решения, основанный на BPNN, соответствует количеству положительных решений для определенного режима движения, обнаруженного для данного кадра по 200 траекториям и нормализованных до 1 или -1 для ограниченных или направленных траекторий, соответственно (черный – ограниченные траектории; серый – направленные траектории).Алгоритм также был протестирован с шумом локализации 30 нм (пунктирные линии на графике). b На верхней панели показана синтетическая траектория продолжительностью 40 с (400 кадров), включая переходное удержание (от 10 до 15 с) диаметром 1 мкм (красный след, увеличенный в красном круге) и переходное направленное движение ( От 30 до 35 с) со скоростью В = 1,2 мкм / с (синяя кривая). Броуновская часть – черным. Коэффициент диффузии D составляет 0,25 мкм ² / с, а время интегрирования 100 мс.Масштабная линейка, 1 мкм. c Нижняя панель представляет собой график зависимости вероятности обнаружения режима движения (выходные значения BPNN) от продолжительности траектории для ограниченного (красный) или направленного (синий) движения. Ограниченные (жирная красная кривая) и направленные (жирная синяя кривая) сегменты обнаруживаются соответственно между 10,0 и 14,6 с и между 30,6 и 35,3 с, как показано серыми линиями. Значения порога обнаружения соответствуют вероятности обнаружения с доверительной вероятностью 95% (см.рис.4). Расчетный диаметр удержания 1,06 мкм

B. Валидация алгоритма

Алгоритм сначала был проверен с использованием 200 синтетических траекторий из 400 кадров, содержащих один сегмент из 50 кадров и удержания, и направленного движения (1 мкм для диаметра ограничения и 1,2 мкм / с для скорости, соответственно ; 100 мс для временного приращения и 0,25 мкм ² / с для коэффициента диффузии), протестировано с или без шума локализации 30 нм.Процент принятия решения на основе BPNN соответствует количеству положительных решений для определенного режима движения, обнаруженного для данного кадра и нормализованного до 1 или -1 для ограниченных или направленных траекторий, соответственно (рис. 4a). Ограниченные и направленные сегменты были обнаружены BPNN с хорошей точностью (99 и 78% обнаружение ограниченных и направленных сегментов в пределах сегмента из 50 кадров). Пример траектории показан на рис. 4b и c. Продолжительность удержания и направленных сегментов были немного недооценены BPNN, соответственно 4.6 с и 4,7 с вместо 5 с. Данные для части траектории, обозначенной как направленная или ограниченная, были соответственно подогнаны с помощью уравнений 2 и 3, описанных в разделе “Методы”. Диаметр удержания и скорость были оценены как 1,06 мкм и 1,2 мкм / с соответственно. Эти значения хорошо согласуются с параметрами моделирования. Как и ожидалось, кажущиеся коэффициенты диффузии из броуновских сегментов оцениваются примерно в 0,25 мкм ² / с. Никаких изменений в решении на основе BPNN при добавлении шума позиционирования 30 нм не наблюдалось.

Мы также оценили способность BPNN обнаруживать небольшие сегменты в пределах траектории. Было создано 200 смоделированных траекторий из 300 кадров, содержащих ограниченные сегменты различной длины, и была рассчитана вероятность обнаружения названного решения на основе BPNN как функция длины сегмента. Аналогичный процесс использовался для режима направленного движения (Дополнительный файл 1: Рисунок S1). Наши результаты показывают, что наш алгоритм способен обнаруживать 99 и 90% ограниченных или направленных режимов движения в пределах сегмента из 40 кадров соответственно.Эти значения упали до 74 и 72% для сегмента из 30 кадров и до 27 и 43% для сегмента из 20 кадров. Процент обнаружения упал ниже 10%, когда длина сегмента меньше 10 кадров. Важно указать, что эта оценка проводилась с параметрами диффузии, близкими к параметрам, часто встречающимся в биологических мембранах (интегрирование по времени 100 мс, коэффициент диффузии частиц 0,25 мкм ² / с, скорость в диапазоне от 1 до 3 мкм / s для направленных траекторий и диаметра удержания от 0.От 5 до 1,2 мкм). Процент обнаружения может быть значительно улучшен для более высокой скорости (60% и 100% обнаружение для V = 4 мкм / с с использованием 10 и 20 кадров соответственно; данные не показаны). Аналогичным образом уменьшение скользящего окна повышает точность обнаружения ограниченных траекторий. Наша цель здесь заключалась в том, чтобы предоставить в качестве доказательства концепции инструмент с эффективным обнаружением как направленных, так и ограниченных участков в пределах одной и той же траектории.

C. Сравнение с другими методами

Как упоминалось во введении, было разработано несколько алгоритмов для сегментации различных типов движения в пределах траекторий.Затем мы сравнили наш метод на основе BPNN с 3 свободно доступными алгоритмами. Два метода основаны на байесовском анализе и специализируются на обнаружении ограниченных (байесовские информационные критерии, названные BIC [16]) или направленных (скрытое марковское моделирование (HMM) -Bayes [17]) сегментов внутри траектории. Третий метод – это метод машинного обучения, основанный на сегментации траектории с использованием классификации контролируемых опорных векторов (SVM) [18]. Сравнение было выполнено с использованием параметров настройки и смоделированных траекторий, аналогичных описанным выше, а именно траектории 300 кадров, включая один сегмент направленного движения и один сегмент ограничения, всегда локализованные в одном и том же положении, оба длиной 50 кадров, скорость изменяется случайным образом. от 1 до 3 мкм / с для направленного движения и одного участка удержания диаметром от 0.5 и 1,2 мкм для ограниченного движения (дополнительный файл 2: рисунок S2). В этих условиях четыре метода оказались очень специфичными с точностью обнаружения более 95% (метод SVM был наиболее специфичным с точностью обнаружения 99,9%). Большие различия наблюдались с точки зрения чувствительности, и наш алгоритм смог обнаружить соответственно 75,3 и 83,1% ограниченных и направленных сегментов из 50 кадров в пределах траектории из 300 кадров (дополнительный файл 2: рисунок S2). Мы также оценили время расчета, которое важно учитывать, поскольку SPT требует большой выборки для получения значимых результатов.Скорее всего, из-за того, что наш алгоритм был разработан в среде Visual C ++, время вычислений было очень низким, обычно менее 1 с для анализа траектории из 300 кадров ( D , 0,25 мкм ² / с; время интегрирования 100 мс) с использованием ПК Windows 7 Intel (R) Core 5TM) i7-2640 M CPU 2,8 ГГц (данные не показаны).

D. Сегментация реальных траекторий

Затем алгоритм был использован для сегментации траекторий, восстановленных из фильмов, записанных в живых клетках. BPNN использовался в контексте отслеживания YFP-меченных вирусов мышиного лейкоза Молони (MLV) в клетках эмбриональной почки человека (HEK) с использованием флуоресцентной микроскопии полного внутреннего отражения (TIRF) (см. Раздел «Методы»).Поведение такой вирусной частицы может быть броуновским, ограниченным, когда она захвачена мембраной клетки-хозяина, или направленным, когда частица экспортируется из цитоплазмы в плазматическую мембрану [26, 27]. Пример такой сложной траектории, чередующейся между различными режимами движения, показан на рис. 5a, а анализ нейронной сетью – на рис. 5b. Алгоритм определяет три различных режима движения по траектории. Ограничение было обнаружено в течение 6,1 с в зоне диаметром 170 нм, что хорошо согласуется с предыдущим отчетом о мышиных вирусоподобных частицах полиомы [28].Направленное движение также наблюдалось в течение 4 с со скоростью 0,38 мкм / с, что хорошо сравнимо с ранее сообщенным для MLV (0,57 мкм / с в [29]). Остальная траектория была броуновской. Мы также протестировали алгоритм BPNN, проанализировав набор траекторий тетраспанина CD9, записанный в клетках HeLa (рис. 6). Эта молекула представляет собой трансмембранный белок, экспрессируемый в плазматической мембране, который, как было продемонстрировано, диффундирует в основном по броуновскому типу, но может временно или постоянно ограничиваться участками мембраны, обогащенными тетраспанинами и их партнерами (rev. [30]).Траектории, включающие временное удержание молекул CD9, называются «смешанными траекториями» из-за комбинации броуновского и ограниченного поведения. Кажущийся коэффициент диффузии 1000 молекул CD9 был сначала определен с использованием первых точек (D _1-4) графика MSD как функции времени (верхняя часть графика разброса на фиг.6, каждая точка представляет одну молекулу). ), а среднее значение кажущегося коэффициента диффузии CD9 (0,23 ± 0,04 мкм ² / с) было аналогично тому, которое ранее сообщалось в плазматической мембране клеток HeLa [31].Интересно, что BPNN смогла непосредственно обнаружить смешанные траектории (синие точки на диаграмме рассеяния на рис. 6) в дополнение к чисто броуновским (зеленый) и чисто ограниченным (красный) траекториям (38,5, 45,6 и 15,9% от общего числа траекторий, соответственно). Эти проценты также хорошо сравниваются с описанными в [31]. Подобно тому, что описано на рис. 6, BPNN предоставил количество кадров каждого идентифицированного сегмента и соответствующий кажущийся коэффициент диффузии (D _1-4).Диаметр удержания, связанный с этими сегментами, был рассчитан на основе анализа MSD, и, в соответствии с предыдущим отчетом, диаметр удержания был меньше для чисто замкнутых траекторий по сравнению с диаметром замкнутого сегмента в смешанных траекториях (215 ± 68 нм против 273 нм). ± 89 нм).

Рис. 5

Анализ режимов движения в пределах реальной траектории частицы вируса мышиного лейкоза Молони (MLV) в клетках HEK. На верхней панели показана траектория частицы MLV, содержащей YFP-меченные белки Gag, записанная в инфицированных клетках 293 HEK, отслеженная с помощью микроскопии TIRF и записанная при времени интеграции 100 мс.Область заключения увеличена красным кружком. Нижняя панель представляет собой график вероятности обнаружения режима движения (выходные значения BPNN) в зависимости от продолжительности траектории. Зона удержания обнаруживается в течение 6,1 с (жирная красная линия) с коэффициентом диффузии 0,01 мкм ² / с и диаметром 170 нм. Направленное движение отображается в течение 4 с с коэффициентом диффузии 0,012 мкм ² / с и скоростью 0,38 мкм / с. Масштабная шкала, 500 нм

Фиг.6

Отслеживание одной молекулы тетраспанина CD9 в клетках HeLa. Панель ( a ) представляет собой DIC-изображение одной клетки HeLa, а красные линии представляют некоторые записанные траектории одиночных молекул (масштабная линейка составляет 5 мкм). Нижняя панель ( b ) представляет графики разброса кажущихся коэффициентов диффузии CD9, рассчитанных на основе анализа MSD 1000 траекторий в клетках HeLa. Каждая точка представляет одну траекторию, а поведение диффузии, которое было определено с помощью нейронной сети BPNN, обозначено цветовым кодом (красный, ограниченный с именем ( c ) зеленый, броуновский с именем ( b ) синий, смешанный с именем M ).Верхний график разброса соответствует совокупности траекторий (названных все). На панели ( c ) показан диаметр удержания, рассчитанный из сегментов удержания, идентифицированных с использованием BPNN для замкнутых и смешанных траекторий

Динамические взаимодействия между мембранно-связывающим белком и липидами вызывают колеблющуюся диффузию

Abstract

Домены гомологии плэкстрина (PH) – это мембранно-связывающие белки распознавания липидов, которые взаимодействуют с молекулами фосфатидилинозитолфосфата (PIP) в мембранах эукариотических клеток.Диффузия доменов PH играет решающую роль в биологических реакциях на поверхности мембран. Хотя коэффициент диффузии можно оценить с помощью длительных измерений, информация о кратковременной диффузной природе отсутствует. Мы выявили два диффузионных свойства домена PH, связанного с поверхностью PIP-содержащей мембраны, с помощью моделирования молекулярной динамики. Одним из них является фракционное броуновское движение, связанное с движением липидов, с которыми взаимодействует домен PH. Другой – изменяющийся во времени коэффициент диффузии; то есть кратковременная диффузия связанного белка существенно изменяется со временем.Более того, коэффициент диффузии для кратковременных измерений существенно отличается от коэффициента диффузии для длительных измерений. Этот колеблющийся коэффициент диффузии является результатом динамических изменений во взаимодействиях между доменом PH и молекулами PIP. Наши результаты свидетельствуют о том, что сложность белок-липидных взаимодействий играет решающую роль в диффузии белков на поверхности биологических мембран. Изменения диффузии PH-доменов и связанных с ними мембраносвязанных белков могут, в свою очередь, способствовать образованию / растворению белковых комплексов в мембранах.

Ключевые слова

Аномальная диффузия
Белки периферической мембраны
Домены гомологии плекстрина
Фосфатидилинозитолфосфат
Моделирование молекулярной динамики

ВВЕДЕНИЕ

Уникальные биологические реакции в клеточных мембранах и комплексах клеток, обеспечивающих как биологические реакции, так и комплексы клеток -липидные и белок-белковые взаимодействия внутри мембран играют ключевую роль ( 1 – 3 ). Диффузия биомолекул внутри мембран имеет решающее значение для регулирования многих аспектов функции клеток.Сложность макромолекул и скученность вызывают пространственно-временную неоднородность и, таким образом, влияют на процесс диффузии в среде клеточных мембран.

Белки периферических мембран присутствуют в цитоплазме клеток и связываются с поверхностями клеточных мембран липид-зависимым образом. Они играют ключевую роль во многих событиях трафика и сигнализации внутри клеток. Ассоциация периферических белков на поверхности мембран определяется липид-связывающими модулями, из которых домены гомологии плекстрина (PH) представляют собой хорошо изученное семейство.Домены PH представляют собой структурно консервативное семейство белков, которые связываются со специфическими липидами [фосфатидилинозитолфосфатами (PIPs)], которые присутствуют в клеточных мембранах ( 4 , 5 ). Хотя структуры и мембранные взаимодействия были изучены для различных PH-доменов ( 6 – 8 ), понимание диффузионного поведения PH-доменов, связанных с поверхностью клеточной мембраны, остается сложной задачей ( 9 – 11 ). Недавно в ряде исследований было высказано предположение, что молекулы PIP группируются вокруг мембраносвязанных периферических белков ( 12 , 13 ).Эта кластеризация может влиять на диффузию периферических белков на поверхности мембран и, таким образом, вероятно, играет роль в регуляции их функции.

Используя методы отслеживания одиночных частиц, можно получить траектории биомолекул. Диффузия часто характеризуется усредненными по времени среднеквадратичными смещениями (TAMSD) (1), где и Δ ( t ) – положение отслеживаемой частицы и время запаздывания, соответственно. В простых процессах диффузии коэффициент диффузии характеризуется наклоном TAMSD для длительных измерений, то есть, где d – размер, а D – коэффициент диффузии.В этом случае коэффициент диффузии определяется однозначно в зависимости от вязкости среды и / или формы броуновской частицы. Однако в живых клетках белки могут менять свою форму, и свойства окружающей среды меняются со временем. Следовательно, коэффициент диффузии, полученный с помощью длительных измерений, не может уловить кратковременный коэффициент диффузии, определяемый как коэффициент диффузии, полученный с помощью кратковременных измерений, который, как считается, по своей природе колеблется в процессе диффузионных процессов.Более того, аномальная диффузия, рассматриваемая как сублинейная зависимость TAMSD от времени, не является чем-то необычным, а скорее повсеместно наблюдается для обоих белков клеточных мембран ( 14 , 15 ) и, например, мРНК ( 16 ), хромосомных локусов ( 17 ), липидных гранул ( 18 ) и гранул инсулина ( 19 ) внутри клеток. Более того, с помощью моделирования молекулярной динамики (МД) субдиффузионные движения также наблюдались при диффузии липидов ( 20 – 23 ), трансмембранных белков ( 24 ) и молекул воды на поверхности мембран ( 25 ).

Различные стохастические модели аномальной диффузии были предложены для интерпретации физического происхождения процесса диффузии в предположении, что окружающая среда однородна ( 26 , 27 ). Однако это предположение маловероятно для клеточной мембраны, которая представляет собой гетерогенную среду ( 3 ). Более того, модель гашеной ловушки, то есть диффузия на случайном энергетическом ландшафте, обеспечивает богатое поведение, которое отличается от поведения однородной среды ( 28 , 29 ).Выявление происхождения диффузии важно, потому что это позволит нам понять физические свойства ряда процессов, например, вязкоупругости при скоплении макромолекул ( 16 , 18 , 20 – 23 , 25 ), кратковременная иммобилизация при наличии препятствий с тяжелым захватом ( 14 , 19 , 25 ) и заклинивание при наличии препятствий ( 14 , 19 ).Диффузия также может изменяться во времени из-за изменений в окружающей среде или из-за динамически изменяющихся форм биомолекул ( 30 , 31 ). Стохастические модели для процессов гетерогенной диффузии, в которых коэффициент диффузии является пространственно-временной случайной величиной, были недавно разработаны для интерпретации аномальной диффузии биомолекул в гетерогенных средах скопления людей [например, пространственная неоднородность ( 32 ) и временная неоднородность ( 33 – 38 )].

Здесь, используя моделирование методом МД, мы исследуем диффузионное поведение PH домена DAPP1 на поверхности липидной мембраны, исследуя, как диффузия белка изменяется во времени. Более того, мы показываем, что флуктуирующая диффузия связанного белка возникает из-за лежащих в основе белок-липидных взаимодействий, которые, в свою очередь, динамически меняются во времени, и что этот процесс является эргодическим.

РЕЗУЛЬТАТЫ

Моделирование взаимодействий PH домена с мембраной

Для исследования процесса диффузии периферического белка на поверхности мембраны мы выполнили крупнозернистое моделирование MD (CG-MD) ( 39 ) DAPP1 PH домен, взаимодействующий с PIP-содержащей двухслойной липидной мембраной.В начальной конфигурации каждой симуляции домен PH был смещен примерно на 100%. 9 нм от поверхности липидного бислоя. Была проведена сотня симуляций, каждое по 10 мкс, начиная с различных начальных ориентаций домена PH относительно бислоя, что привело к общему времени моделирования 1 мс. Мы отслеживали белок на поверхности мембраны и анализировали диффузию домена PH для последних 8 мкс каждой траектории, по которой белок был связан с мембраной (см. Рис. S1). Обратите внимание, что 3 траектории были удалены из первоначального ансамбля из 100, поскольку молекула белка, связавшись, впоследствии диссоциировала от бислоя.Кроме того, мы вычли центр масс (COM) связанного двухслойного листочка из траекторий белка, чтобы устранить эффекты движения COM мембраны в целом ( 20 , 22 , 24 , 25 ). TAMSD домена PH на поверхности липидной мембраны обнаруживает временную субдиффузию, то есть при более коротких временах задержки переключение на более длительные времена задержки (см. Рис. 1). Показатель степени α изменяется от 0,7 до 1,0 в точке кроссовера около 10 нс, что соответствует точке кроссовера для аномальной диффузии липидов внутри чистых липидных бислоев ( 20 – 24 ).Обратите внимание, что коэффициент диффузии имеет тот же порядок величины, что и экспериментально измеренный коэффициент диффузии PH домена GRP1 ( 9 , 10 , 13 ). Подобная временная субдиффузия наблюдается и для других PH доменов ( 13 ). Более того, мы подтвердили, что нет старения TAMSD, то есть, и что существует эргодичность процесса диффузии, то есть усредненное по ансамблю MSD согласуется с TAMSD (см. Рис. S2).

Инжир.1 TAMSD 97 траекторий домена PH на поверхности мембраны.

Время измерения для каждой траектории t составляет 8 мкс. Сплошные черные линии показаны для справки.

Антикоррелированное движение домена PH в более коротких временных масштабах

Известно, что диффузионные свойства липидов демонстрируют коррелированные движения, соответствующие фракционному броуновскому движению (FBM) ( 20 – 23 ). Было также показано, что коррелированные движения липидов влияют на динамику межфазных молекул воды на поверхности мембраны ( 25 , 40 ).Чтобы исследовать влияние FBM липидных молекул на домен PH, мы рассчитали автокорреляционную функцию смещения (DAF) белка (2)

На рисунке 2A показано нормализованное DAF C _Δ ( t ) / C _Δ (0) для Δ = 0,1 и 2 нс. DAF свободных FBM затухает от отрицательных значений до нуля по степенному закону ( 41 ), C _Δ ( t ) / C _Δ (0) ~ – (α – α ²) (Δ / t ) ^{2 – α}/2.Нормированный DAF для Δ = 0,1 нс хорошо согласуется с теоретическим поведением свободного FBM с α = 0,7 ( 41 ). Хотя нормализованный DAF для Δ = 2 нс не согласуется с FBM, мы можем ясно видеть отсечку около 10 нс, что означает, что TAMSD соответствуют нормальной диффузии для Δ> 10 нс. Поведение белка демонстрирует антикорреляцию, сравнимую с антикоррелированными движениями липидов ( 20 – 23 ). Таким образом, процесс диффузии периферического белка PH на поверхности мембраны в более коротких временных областях зависит от FBM липидов, с которыми он взаимодействует.

Рис. 2 Антикоррелированное движение и негауссовость домена PH, диффундирующего по поверхности мембраны.

( A ) Нормализованный DAF C _Δ ( t ) / C _Δ (0) белка для Δ = 0,1 нс (черный) и 2 нс (желтый). На вставке показан график журнала. Сплошные и пунктирные голубые линии обозначают теорию FBM. ( B ) Зависимость пропагатора от нормализованного положения, определяемого как, где SD σ равны 0.1, 0,6 и 5,4 нм для Δ = 10 ⁻⁴, 10 ⁻² и 1 мкс соответственно. Каждый другой символ представляет различное время задержки Δ. Пунктирная линия – гауссово распределение с единичной дисперсией. Пропагаторы отклоняются от гауссовости при x > 4σ.

Чтобы подтвердить, хорошо ли описываются диффузионные особенности FBM, мы исследовали гауссовость смещения. В частности, мы вычислили пропагатор, то есть вероятность того, что частица будет найдена в ( x , x + dx ) во время задержки Δ.Однако нормализованный пропагатор P ( x , Δ) имеет негауссову форму (см. Рис. 2B). Следовательно, аномальная диффузия домена PH может быть объяснена сосуществованием с другими диффузионными свойствами.

Неустойчивая диффузия домена PH

Взаимодействия между белком и молекулами PIP в бислое имеют решающее значение для локализации домена PH на поверхности мембраны. Как показано на фиг. 3A, количество молекул PIP, взаимодействующих со связанным доменом PH, изменяется со временем.Ожидается, что эти динамические взаимодействия будут влиять на диффузионность белка, потому что диффузия в значительной степени зависит от свойств комплекса PH / PIP, включая количество PIP, присутствующих в этом комплексе. Другими словами, кратковременный коэффициент диффузии (соответствующий краткосрочному, то есть субнаносекундному, субдиффузионному режиму) может изменяться со временем по мере изменения количества связанных PIP. Чтобы лучше охарактеризовать диффузионное поведение домена PH, мы предлагаем новый метод оценки кратковременной диффузии.Насколько нам известно, в настоящее время не существует метода оценки кратковременного коэффициента диффузии без знания моментов, в которые коэффициент диффузии существенно изменяется. Используя наш метод оценки (см. «Материалы и методы» для более подробной информации), мы можем обнаружить вариации кратковременной диффузии в зависимости от времени на траектории (см. Рис. 3B). Здесь мы получили пять различных диффузионных состояний за время моделирования. Таким образом, мы успешно обнаружили флуктуирующий коэффициент диффузии домена PH.Чтобы исследовать влияние кластеризации PIP вокруг домена PH на диффузионную способность белка, мы рассчитали количество PIP, связанных доменом PH в каждом диффузионном состоянии (см. Рис. 3B). Затем мы исследовали корреляцию между зависящим от времени коэффициентом диффузии [ D ( t )] и количеством связанных PIP во всем ансамбле из 97 проанализированных симуляций [см. Рис. 3C; функции плотности вероятности (PDF) D ( t ) и показаны на рис.S3]. Очевидно, что коэффициент диффузии белка ниже, когда связано больше PIP, чем когда связано меньше PIP. Существует отрицательная корреляция (коэффициент корреляции = -0,42) между кратковременной диффузией и количеством связанных молекул PIP. На рис. 3D мы показываем типичную траекторию домена PH, связанного с поверхностью мембраны, соответствующую рис. 3B. Хотя домен PH диффундирует в одном и том же месте, коэффициент кратковременной диффузии отличается. Это означает, что кратковременная диффузия домена PH претерпевает временные колебания, зависящие не от пространственной неоднородности, а вместо этого от временных изменений количества связанных молекул PIP.

Рис. 3. Неоднородный во времени процесс диффузии домена PH.

( A ) Снимки домена PH в состоянии, связанном с множеством PIP (вверху) и состоянии, связанным с несколькими PIP (внизу). Домен PH, липидный бислой и связанный PIP окрашены в желтый, серебристый и голубой / красный цвета соответственно. ( B ) Временные ряды кратковременной диффузии, оцененные нашим методом, и усредненное по времени количество связанных PIP, соответствующих диффузному состоянию. ( C ) Корреляция между коэффициентом кратковременной диффузии и количеством связанных PIP в каждом состоянии.( D ) Боковая траектория домена PH на поверхности мембраны. Цвета траектории соответствуют каждому состоянию в (B). Черные треугольники указывают начальную и конечную точки.

Неоднородная диффузия с флуктуирующим коэффициентом диффузии

Если система неэргодична и / или среднее значение по времени не берется в течение достаточно длительного периода времени, TAMSD не совпадает с MSD. В этом случае TAMSD демонстрирует широкое рассеяние. Величину флуктуаций TAMSD можно количественно оценить с помощью относительного стандартного отклонения (RSD) ( 36 – 38 , 42 – 44 ) (3)

В случае неэргодических процессов диффузии Например, случайное блуждание в непрерывном времени ( 42 – 44 ) и модели с отожженным временем прохождения ( 35 ), RSD TAMSD сходится к ненулевому значению для всех Δ ≪ t как t → ∞.Это полностью отличается от процессов эргодической диффузии, например, броуновского движения и FBM в случае субдиффузии ( 45 ), для которых RSD сходится к 0 со степенной формой t ^−0,5. В этом случае не было бы существенных различий между коэффициентами диффузии для кратковременных и длительных измерений. Другими словами, колебания TAMSD происходят из-за конечного времени измерения. Однако отличие от масштабирования t ^−0.5 подразумевает возможность того, что коэффициент кратковременной диффузии по своей природе колеблется. На рис. 4 показано RSD TAMSD мембраносвязанного домена PH. Сходимость RSD к 0 происходит очень медленно, то есть показатель степени ниже -0,5, хотя процесс диффузии является эргодическим, как показано соглашением между усредненными по времени и усредненными по ансамблю MSD (см.рис. S2).

Рис. 4 RSD TAMSD белка (обозначено «•»).

Сплошная красная линия представляет RSD TAMSD модели LEFD с γ = 0.6, τ _c = 10 мкс, D _F = 17 мкм ² / с и D _S = 14 мкм ² / с. Сплошная черная линия показана для справки.

Чтобы интерпретировать это, мы рассматриваем уравнение Ланжевена с моделью флуктуирующей диффузии (LEFD) ( 36 – 38 ) как неоднородный во времени процесс диффузии, где ω ( t ) – белый гауссов шум с 〈ω ( t )〉 = 0, а 〈ω ( t ) ω ( t ′)〉 = δ ( t – t ′).Модель LEFD является разумной, поскольку было показано, что домен PH демонстрирует быструю и медленную диффузионную способность в зависимости от количества связанных PIP (см. Выше), а процесс диффузии в этой модели является эргодическим. Чтобы уловить существенные особенности наблюдаемой гетерогенной диффузии, мы считаем, что коэффициент диффузии D ( t ) изменяется дихотомически, то есть D _S для медленного состояния и D _F для быстрого состояния ( D _S < D _F).Из PDF коэффициента диффузии для Δ = 0,1 мкс и t = 1 мкс мы использовали D _F = 17 и D _S = 14 мкм ² / с (см. рис. S4). В LEFD с моделью с двумя состояниями время пребывания для каждого состояния является случайной величиной, и мы предполагаем, что эти распределения следуют степенным распределениям с экспоненциальными отсечениями, ρ (τ) ~ τ ^{−1 − γ} exp (- τ / τ _c), а γ = 0,6 было взято из предыдущего исследования ( 13 ) (см.рис.S5), который исследовал состояния, связанные с множеством PIP и с несколькими состояниями, связанными с PIP. Как видно из рис. 4, RSD модели LEFD неожиданно согласуется с RSD моделированием MD домена PH (τ _c = 10 мкс было подогнано с RSD домена PH) . Более того, PDF коэффициента диффузии и негауссовский пропагатор модели LEFD аналогичны таковым для области PH (см. Рис. S6). Это еще одно свидетельство того, что коэффициент кратковременной диффузии по своей природе колеблется со временем.Во многих процессах передачи сигналов могут потребоваться динамические взаимодействия периферических и интегральных мембранных белков. Таким образом, флуктуирующая диффузия PH-доменов и изменения в их локальном липидном окружении могут вносить вклад в динамику образования / растворения сигнальных комплексов и / или рекрутирования / отсоединения других периферических мембранных белков на мембране.

ОБСУЖДЕНИЕ

Таким образом, мы использовали обширное (1 мс) моделирование MD для исследования диффузионных свойств PH домена DAPP1, связанного с поверхностью модельной клеточной мембраны.Хотя лежащий в основе процесс диффузии является эргодическим, коэффициент диффузии белка аномально колеблется, что может быть связано с динамическим взаимодействием между доменом PH и молекулами PIP, с которыми он связан.

Клеточные мембраны представляют собой пространственно и временно неоднородную среду вследствие образования липидных (нано) доменов, скопления различных видов липидов и белков и взаимодействия с цитоскелетными компонентами клетки ( 3 ).Эти компоненты мембранной среды регулируются во времени и пространстве. Динамические взаимодействия мембранных белков с липидами добавляют дополнительный уровень сложности, что, как ожидается, сделает процесс диффузии мембранных белков еще более гетерогенным. В нашем исследовании мы показали, что эта гетерогенность определяет диффузионную природу ключевых периферических белков на поверхности мембран. В частности, количество молекул PIP, которые связаны с доменом PH, изменяет его коэффициент диффузии.Также вероятно, что события ассоциации / диссоциации могут добавить дополнительный уровень сложности к динамике белка на поверхности мембраны. Однако, поскольку мы наблюдали только три таких события в ансамбле 100 × 10 мкс, мы не можем надежно количественно оценить последствия процесса диссоциации / ассоциации. Эти гетерогенные диффузионные процессы могут иметь решающее значение для множества биологических процессов ( 46 , 47 ). Наши результаты также предполагают, что липидные молекулы не только действуют как якоря для доменов PH, но также могут обеспечивать механизм, который регулирует их функцию, контролируя их диффузию и, таким образом, потенциально модулируя их взаимодействия с другими белками и рецепторами.Возможно, что другие классы периферических белков, которые взаимодействуют со специфическими липидами [например, домены C2 ( 48 ) и PTEN ( 49 )] могут демонстрировать сравнимое диффузионное поведение.

МАТЕРИАЛЫ И МЕТОДЫ

Моделирование методом МД

Моделирование методом КГ-МД было выполнено с использованием GROMACS 4.5.5 ( 50 ) с силовым полем Мартини 2.1 ( 51 , 52 ). Используемый в моделировании бислой состоял из POPC (1-пальмитоил-2-олеоил- sn -глицеро-3-фосфохолин) / POPS (1-пальмитоил-2-олеоил- sn -глицеро-3-фосфо-1 -серин) / PIP ₂ (фосфатидилинозитол-4,5-бисфосфат) / PIP ₃ (фосфатидилинозитол-3,4,5-трифосфат) [259 POPC (73%), 71 POPS (20%), 18 PIP ₂ (5%) и 8 молекул PIP ₃ (2%)].Системы сольватировали 14000 молекул воды CG и добавляли ионы NaCl в концентрации 150 мМ для нейтрализации системы. Все системы были минимизированы по энергии на 200 шагов и уравновешены в течение 1 нс с удерживаемыми частицами белковой цепи. Для каждого повторения симуляции в ансамбле белок произвольно вращался вокруг осей x , y и z , чтобы сформировать новую начальную конфигурацию. Для динамики диффузии белка было выполнено 100 симуляций по 10 мкс (общее время моделирования 1 мс) с доменом DAPP1 PH [код банка данных белка: 1FAO ( 53 )] с шагом по времени 20 фс, траектории были сохраняется каждые 0.1 нс. Для каждого моделирования данные от 0 до 2 мкс отбрасывались перед сбором данных от 2 до 10 мкс для анализа диффузии домена PH. Таким образом, каждый анализ моделирования начинается с различного распределения молекул PIP вокруг домена PH (см. Рис. S7). Модель упругой сети была применена ко всем частицам основной цепи в пределах расстояния отсечки 0,7 нм для моделирования вторичных и третичных структур ( 54 ). Длины связей были ограничены до равновесных длин с использованием алгоритма LINCS (Linear Constraint Solver) ( 55 ).Взаимодействия Леннарда-Джонса были сдвинуты к нулю между 0,9 и 1,2 нм, а кулоновские взаимодействия были сдвинуты к нулю между 0 и 1,2 нм. Давление 1 бар и температура 323 К контролировались с помощью алгоритма Берендсена ( 56 ) со временем взаимодействия 1 пс. Вышеупомянутый метод предсказывает правильный DAPP1 PH / двухслойный комплекс, как мы показали в предыдущей работе ( 8 ). В этой работе мы исследовали локализацию 13 различных доменов PH на поверхности модельной липидной мембраны с использованием подхода многомасштабного моделирования.Поразительно, что комплексы PH / PIP, полученные с помощью нашего моделирования, аналогичны комплексам, полученным с помощью рентгеновской кристаллографии или ядерного магнитного резонанса.

Оценка кратковременного коэффициента диффузии

Здесь мы ввели метод оценки для определения кратковременного коэффициента диффузии. Этапы нашего метода были следующими: Сначала мы рассчитали TAMSD, ограниченный временным окном [ t , t + T – Δ], и, таким образом, мы получили временные коэффициенты диффузии как функцию t (4) где T – параметр, который мы должны были определить соответствующим образом.Здесь мы использовали Δ = 0,1 мкс и T = 1 мкс, которые были теми же значениями, которые использовались для расчета коэффициента диффузии на рис. S3. Однако при этом не удалось уловить кратковременный коэффициент диффузии, потому что некоторое временное окно [ t , t + T – Δ] содержало точку, в которой кратковременный коэффициент диффузии существенно изменился. По этой причине мы ввели время обновления, при котором изменяется коэффициент диффузии. Время обновления определялось как временные коэффициенты диффузии, пересекающие его среднее значение.Мы разделили полученную траекторию D ( t ; Δ, T ) на два состояния: быстрое состояние F и медленное состояние S , используя среднее значение, рассчитанное по всей траектории. Точка перехода t _i каждого состояния была оценена как S → F [ρ _S ( t _i) <ρ _F ( t _i)] или F → S [ρ _F ( t _i) <ρ _S ( t _i) )], где (5) (6) использовали среднее значение D _a, а мы использовали T _c = 10 нс.Время обновления определяет точку перехода от быстрого диффузионного состояния к медленному или наоборот. Поскольку мы знали время обновления t ₁, ⋯, t _i, мы рассчитали кратковременный коэффициент диффузии во временном окне [ t _i, t _{i +1}] (7) где t _i – время восстановления i -е, и мы использовали Δ = 0,1 нс.

ДОПОЛНИТЕЛЬНЫЕ МАТЕРИАЛЫ

Дополнительные материалы к этой статье доступны по адресу http: // advance.sciencemag.org/cgi/content/full/3/1/e1601871/DC1

рис. S1. Расстояние между COM белка и бислоем для 100 повторений моделирования.

рис. S2. Эргодичность диффузионного процесса.

рис. S3. Кратковременная диффузия домена PH и количество связанных молекул PIP.

рис. S4. PDF коэффициента диффузии, рассчитанный для Δ = 0,1 мкс и t = 1 мкс.

рис. S5. PDF времен нахождения состояний, связанных с множеством PIP и с несколькими состояниями, связанными с PIP.

рис. S6. Стохастическое моделирование модели LEFD.

рис. S7. Молекулы PIP вокруг домена PH.

Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии правильного цитирования оригинальной работы.

Благодарности: Финансирование: Эта работа была поддержана грантом MEXT (Министерство образования, культуры, спорта, науки и технологий) для «Программы для ведущих аспирантур» и грантом докторантуры Университета Кейо. Программа помощи.A.C.K. и M.S.P.S. были профинансированы Wellcome Trust, номер гранта WT092970MA. Вклад авторов: E.Y. и Т.А. выполнил расчет и анализ. Представленное здесь исследование явилось результатом оживленных дискуссий между всеми авторами. Все авторы внесли свой вклад в написание рукописи. Конкурирующие интересы: Авторы заявляют, что у них нет конкурирующих интересов. Доступность данных и материалов: Все данные, необходимые для оценки выводов в статье, представлены в документе и / или дополнительных материалах.Дополнительные данные, относящиеся к этой статье, могут быть запрошены у авторов.

Фрактальная модель аномальной диффузии

Проанализируем фрактальную размерность траектории случайного блуждания частицы. Фрактальная размерность траектории в полностью развитом броуновском движении равна 2. Если мы рассмотрим случайное блуждание, длина свободного пробега которого не пренебрежимо мала, траекторию можно охарактеризовать фрактальной размерностью, зависящей от масштаба. Наблюдая в масштабе, намного меньшем, чем длина свободного пробега, можно обнаружить, что траектория почти прямая (Kneller 2011).В противном случае случайное блуждание может быть сведено к броуновскому движению при достаточно большом анализе (Bujan-Nuňez 1998; Matsuura et al. 1986; Rapaport 1984, 1985; Такаясу 1990).

Зависящая от масштаба ( s ) фрактальная размерность для траектории случайного блуждания, заданная в общем виде для трехмерного пространства (Bujan-Nuňez 1998), составляет:

$$ D_ {w} \ left (s \ right) = 2 – \ frac {1} {1 + s / k \ varLambda} $$

(2)

, где k – константа пропорциональности, являющаяся подгоночным членом, а Λ – длина свободного пробега частицы.Соответственно, D _w ( s ) изменяется от 1, если \ (s / k \ varLambda \ to 0 \), и 2, если \ (s / k \ varLambda \ to \ infty \). Чем больше масштаб наблюдения, тем ближе случайное движение к броуновскому движению.

Первый член в правой части уравнения. (2) – асимптотическая фрактальная размерность броуновской траектории. В очень маленьком масштабе наблюдения фрактальная размерность равна единице, потому что знаменатель второго члена равен единице, а затем увеличивается, приближаясь к своему асимптотическому значению, когда знаменатель второго члена стремится к бесконечности.Таким образом, первый член равен D . _w, асимптотическое значение фрактальной размерности траектории, а начальное значение дроби – D _w – 1. Это налагает форму обобщенной формулы.

Формула теперь обобщена для описания зависящей от масштаба фрактальной размерности с скорректированным асимптотическим значением

$$ D _ {\ text {w}} \ left (s \ right) = D _ {\ text {w}} – \ гидроразрыв {{D _ {\ text {w}} – 1}} {1 + s / k \ varLambda} $$

(3)

дает то же значение, 1, характерное для баллистического движения, если \ (s / k \ varLambda \ to 0 \), но требуемое значение D _w, вместо 2, если \ (s / k \ varLambda \ to \ infty \).Эта формула должна описывать переход характера траектории частицы от баллистической к характеристике аномальной диффузии. Этот подход рассматривает броуновское движение как частный случай, для которого фрактальная размерность траектории стремится к 2 для больших масштабов наблюдения. Это означает, что поставив D _w = 2 в уравнение. (3) дает уравнение. (2). Путь Д _w = 1 в уравнение. (3) получается D _w ( s ) = 1, что подтверждает баллистический характер движения во всем диапазоне шкалы наблюдения.{{D _ {\ text {w}} – 1}}}} $$

(6)

L (0) – длина контура траектории, равная сумме длин отрезков линии. Частица или молекула движется по отрезку с постоянной скоростью V ₀. {1/2} = \ lambda \ frac {t} {\ tau} = v_ {0} t , $$

(14)

независимо от значения фитинга к .{{\ frac {2 – \ alpha} {\ alpha}}} \ cdot \ frac {t} {\ tau} $$

(22)

Среднеквадратичные смещения положения молекулы, нормированные квадратом длины свободного пробега как функция нормированного времени, показаны на рис. 1 для различных показателей аномальной диффузии. Это уравнение, дающее взаимозависимость 〈 r ²〉 / λ ² и t / τ , также позволяет изобразить нормированное среднеквадратичное смещение положения молекулы в двух измерениях 〈 r ²〉 / 4 Γ t как функция нормированного времени.{- \ alpha} $$

(23)

Это сделано на рис. 2 для различных показателей субдиффузии.

Рис. 1

Среднеквадратичные смещения положения молекулы, нормированные квадратом длины свободного пробега в зависимости от нормированного времени, изображенные для различных показателей аномальной диффузии в соответствии с формулой. (22). Прямые соответствуют асимптотическому броуновскому и баллистическому движениям

Фиг.{2 – \ alpha} $$
(26)
Уравнение (25) дает полное описание траектории аномально диффундирующей молекулы, независимо от стадии движения. In может использоваться в качестве детерминанта развития аномальной диффузии и может использоваться для определения коэффициента переноса Γ и показателя аномальной диффузии α из экспериментальных 〈 r ²〉 данные.{1/2}}} {{v_ {0} t}} = 1 $$
(27)
Уравнение (26) описывает изменение во времени среднего квадрата смещения положения частицы или молекулы в двух измерениях в зависимости от значений коэффициента переноса, показателя аномальной диффузии и значения средней скорости частицы в два измерения.