Теплопроводность особенности – – 20108-4

Теплопроводность и другие характеристики строительных материалов в цифрах

Л юбые строительные работы начинаются с создания проекта. При этом планируется как расположение комнат в здании, так и рассчитываются главные теплотехнические показатели. От данных значений зависит, насколько будущая постройка будет теплой, долговечной и экономичной. Позволит определить теплопроводность строительных материалов – таблица, в которой отображены основные коэффициенты. Правильные расчеты являются гарантией удачного строительства и создания благоприятного микроклимата в помещении.

Чтобы дом был теплым без утеплителя потребуется определенная толщина стен, которая отличается в зависимости от вида материала

Теплопроводность представляет собой процесс перемещения тепловой энергии от прогретых частей к холодным. Обменные процессы происходят до полного равновесия температурного значения.

Процесс теплопередачи характеризуется промежутком времени, в течение которого выравниваются температурные значения. Чем больше времени проходит, тем ниже теплопроводность строительных материалов, свойства которых отображает таблица. Для определения данного показателя применяется такое понятие как коэффициент теплопроводности. Он определяет, какое количество тепловой энергии проходит через единицу площади определенной поверхности. Чем данный показатель больше, тем с большей скоростью будет остывать здание. Таблица теплопроводности нужна при проектировании защиты постройки от теплопотерь. При этом можно снизить эксплуатационный бюджет.

Полезный совет! При постройке домов стоит использовать сырье с минимальной проводимостью тепла.

От чего зависит величина теплопроводности?

От множества факторов зависит значение теплопроводности строительных материалов. Таблица коэффициентов, представленная в нашем обзоре, это наглядно показывает.

На данный показатель оказывают влияние следующие параметры:

• более высокая плотность способствует прочному взаимодействию частиц друг с другом. При этом уравновешивание температур производится более быстро. Чем плотнее материал, тем лучше пропускается тепло;
• пористость сырья свидетельствует о его неоднородности. При перемещении тепловой энергии через подобную структуру охлаждение будет небольшим. Внутри гранул находится только воздух, который обладает минимальным количеством коэффициента. Если поры маленькие, то при этом затрудняется передача тепла. Но повышается значение теплопроводность;
• при повышенной влажности и промокании стен здания показатель прохождения тепла будет выше.

Использование значений теплопроводности на практике

Материалы, используемые в строительстве, могут быть конструкционными и теплоизолирующими.

Самое большое значение теплопроводности у конструкционных материалов, которые используются при возведении перекрытий, стен и потолков. Если не использовать сырье с теплоизолирующими свойствами, то для сохранения тепла потребуется монтаж толстого слоя .

Поэтому при возведении постройки стоит использовать дополнительные материалы. При этом значение имеет теплопроводность строительных материалов, таблица показывает все значения.

Полезная информация! Для построек из древесины и пенобетона не обязательно использовать дополнительное утепление. Даже применяя низкопроводной материал, толщина сооружения не должна быть менее 50 см.

Особенности теплопроводности готового строения

Планируя проект будущего дома, нужно обязательно учесть возможные потери тепловой энергии. Большая часть тепла уходит через двери, окна, стены, крышу и полы.

Если не выполнять расчеты по теплосбережению дома, то в помещении будет прохладно. Рекомендуется постройки из , бетона и камня дополнительно утеплять.

Полезный совет! Перед тем как утеплять жилище, необходимо продумать качественную гидроизоляцию. При этом даже повышенная влажность не повлияет на особенности теплоизоляции в помещении.

Разновидности утепления конструкций

Теплое здание получится при оптимальном сочетании к

ruscos.ru

9. Теплопроводность

1. /4 курс/Mенеджмент.doc 2. /4 курс/_стор_я _нженернох д_яльност_.doc 3. /4 курс/Безпека життєд_яльност_.doc 4. /4 курс/Г_дравл_ка, г_дро- та пневмопривод.doc 5. /4 курс/Детал_ машин.pdf 6. /4 курс/Електротехн_ка, електрон_ка _ м_кропроцесорна техн_ка.doc 7. /4 курс/Конструкц_х кол_сних та гусеничних транспортних засоб_в.doc 8. /4 курс/М_кроеконом_ка.rtf 9. /4 курс/Основи еколог_х.doc 10. /4 курс/Основи наукових досл_джень.doc 11. /4 курс/Основи технолог_х виробництва кол_сних та гусеничних транспортних засоб_в.doc 12. /4 курс/Теоретические основы теплотехники/Конспект лекций/ОТТ. Тема 10c. Кратко.doc 13. /4 курс/Теоретические основы теплотехники/Конспект лекций/ОТТ. Тема 11c. Кратко.doc 14. /4 курс/Теоретические основы теплотехники/Конспект лекций/ОТТ. Тема 12c. Кратко.doc 15. /4 курс/Теоретические основы теплотехники/Конспект лекций/ОТТ. Тема 13с. Кратко.doc 16. /4 курс/Теоретические основы теплотехники/Конспект лекций/ОТТ. Тема 14с. Кратко.doc 17. /4 курс/Теоретические основы теплотехники/Конспект лекций/ОТТ. Тема 15с Кратко.doc 18. /4 курс/Теоретические основы теплотехники/Конспект лекций/ОТТ. Тема 1с. Кратко моя.doc 19. /4 курс/Теоретические основы теплотехники/Конспект лекций/ОТТ. Тема 1с. Кратко.doc 20. /4 курс/Теоретические основы теплотехники/Конспект лекций/ОТТ. Тема 2с. Кратко.doc 21. /4 курс/Теоретические основы теплотехники/Конспект лекций/ОТТ. Тема 3с. Кратко.doc 22. /4 курс/Теоретические основы теплотехники/Конспект лекций/ОТТ. Тема 4c. Кратко.doc 23. /4 курс/Теоретические основы теплотехники/Конспект лекций/ОТТ. Тема 5c. Кратко.doc 24. /4 курс/Теоретические основы теплотехники/Конспект лекций/ОТТ. Тема 6с. Кратко.doc 25. /4 курс/Теоретические основы теплотехники/Конспект лекций/ОТТ. Тема 7c. Кратко.doc 26. /4 курс/Теоретические основы теплотехники/Конспект лекций/ОТТ. Тема 8c. Кратко.doc 27. /4 курс/Теоретические основы теплотехники/Конспект лекций/ОТТ. Тема 9с. Кратко.doc 28. /4 курс/Теоретические основы теплотехники/Метод. ТОТзаочн.doc 29. /4 курс/Теоретические основы теплотехники/Раб. пр. ТОТ.doc

10. Конвективный теплообмен Методичні вказівки та індивідуальні завдання Програма навчальної дисципліни Основи наукових дослiджень та технiка експерименту Методичні вказівки та контрольні завдання для студентів заочної Методичні вказівки до виконання індивідуальних робіт з дисципліни «Мікроекономіка» Тематика індивідуальних завдань з дисципліни «Мікроекономіка» Методичні вказівки та індивідуальні завдання до вивчення дисципліни «Конструкції колісних та гусеничних транспортних засобів» для студентів напряму 050503 машинобудування /Укл.: В. К. Сидоренко, О. М. Лосіков. Дніпропетровськ: нметАУ, 2012. 50 с Методичні вказівки до вивчення дисципліни «Електротехніка, електроніка і мікропроцесорна техніка», література, пояснення до виконання індивідуальних завдань Методичні вказівки до вивчення матеріалу кожної теми та наводяться запитання для контролю якості засвоєння тем. Даються методичні вказівки до виконання контрольної роботи, а також варіанти вихідних даних для неї Методичні вказівки і індивідуальні завдання з дисципліни «Історія інженерної діяльності» для студентів спеціальностей 090202, 090218, 092301 Методичні вказівки до самостійного вивчення тем, передбачених програмою дисципліни «Mенеджмент», завдання до контрольної роботи та методичні вказівки до її виконання Тема 14. Газообразное топливо и его сжигание 11. Теплообмен излучением 12. Сложный теплообмен Топливо и его характеристики 13 Виды топлива и их особенности Закон термодинамики Тема термодинамические процессы Тема основные термодинамические понятия и законы Тема основные термодинамические понятия и законы Тема теплоёмкость газов Тема 15. Твердое и жидкое топливо и их сжигание >15 Расчет горения твердого и жидкого топлива Для расчета процессов горения твердого и жидкого топлива составляют материальный баланс процесса горения Закон термодинамики 6. Теоретические основы теплотехники 1998г 7. Тепловые двигатели 8. Теоретические основы теплотехники 1998г 9. Теплопроводность Методичні вказівки та індивідуальні завдання до вивчення дисципліни “Теоретичні основи теплотехніки” для студентів спеціальностей 090202, 090218 Національна металургійна академія україни

Тема 9. Теоретические основы теплотехники 1998г.
9. Теплопроводность

9.1. Основные понятия и определения

Теория теплопередачи, или теплообмена, представляет собой учение о процессах распространения теплоты в пространстве с неоднородным полем температур.

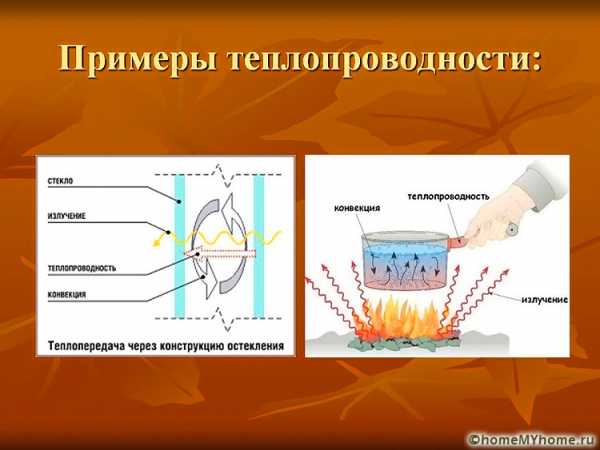
Существуют три основных вида теплообмена: теплопроводность, конвекция и тепловое излучение.

Теплопроводность — это молекулярный перенос теплоты между непосредственно соприкасающимися телами или частицами одного тела с различной температурой, при котором происходит обмен энер­гией движения структурных частиц (молекул, атомов, свободных электронов).

Конвекция осуществляется путем перемещения в пространстве не­равномерно нагретых объемов среды. При этом перенос теплоты не­разрывно связан с переносом самой среды.

Тепловое излучение характеризуется переносом энергии от одного тела к другому электромагнитными волнами.

Часто все способы переноса теплоты осуществляются совместно. Например, конвекция всегда сопровождается теплопроводностью, так как при этом неизбежно соприкосновение частиц, имеющих различные температуры.

Совместный процесс переноса теплоты конвекцией и теплопроводностью называется конвективным теплообменом. Частным случаем конвективного теплообмена является теплоотдача — конвективный теп­лообмен между твердой стенкой и движущейся средой. Теплоотдача может сопровождаться тепловым излучением. В этом случае перенос теплоты осуществляется одновременно теплопроводностью, конвек­цией и тепловым излучением.

Многие процессы переноса теплоты сопровождаются переносом вещества — массообменном, который проявляется в установлении рав­новесной концентрации вещества.

Совместное протекание процессов теплообмена и массообменна называется тепломассообменном.

Теплопроводность определяется тепловым движением микрочастиц тела. В чистом виде явление теплопроводности наблюдается в твердых телах, неподвижных газах и жидкостях при условии невозможности возникновения в них конвективных токов.

Передача теплоты теплопроводностью связана с наличием разности температур тела. Совокупность значений темпера­тур всех точек тела в данный момент времени называется температур­ным полем. В общем случае уравнение температурного поля имеет вид:

, (9.1)

где t — температура тела; х, у, z — координаты точки;  — время. Такое температурное поле называется нестационарным и отвечает неустановившемуся режиму теплопроводности. Если температура тела не изменяется с течением времени, то температурное поле называется стационарным. Тогда

, . (9.2)

Температура может быть функцией одной, двух и трех координат, соответственно температурное поле будет одно-, дву- и трехмерным. Наиболее простой вид имеет уравнение одномерного стационарного температурного поля:

; ; .

Если соединить все точки тела с одинаковой температурой, то полу­чим поверхность равных температур, называемую изотермической. Так как в определенной точке тела в данный момент времени может быть только одна температура, изотермические поверхности не пересекаются; все они либо замыкаются на себя, либо заканчиваются на границе тела. Пере­сечение изотермных поверхностей плоскостью дает на ней семейство изотерм. Интенсивность изменения температуры в каком-либо направлении характеризуется производной , принимающей наибольшее значение в направлении нормали к изотермической поверхности

. (9.3)

Вектор называется температурным градиентом и является мерой интенсивности изменения температуры в направлении по нормали к изотермной поверхности. Направлен он в сторону возрастания температуры.

9.2. Закон Фурье

Согласно гипотезе Фурье, количество теплоты d²Q_, проходящее через элемент изотермической поверхности dF за промежуток времени d, пропорционально температурному градиенту :

. (9.4)

Здесь множитель  называется коэффициентом теплопроводности. Знак минус указывает на то, что теплота передается в направлении умень­шения температуры. Количество теплоты, прошедшее в единицу вре­мени через единицу изотермической поверхности, называется плотностью теплового потока:

. (9.5)

Проекции вектора q на координатные оси соответственно:

; ; .

Уравнения (9.4) и (9.5) являются математическим выражением основного закона теплопроводности — закона Фурье.

Количество теплоты, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком:

. (9.6)

Полное количество теплоты, прошедшее через эту поверхность за время , определится из уравнения

. (9.7)

9.3. Коэффициент теплопроводности

Коэффициент теплопроводности является физическим параметром вещества, характеризующим его способность проводить теплоту. Коэф­фициент теплопроводности определяется из уравнения (9.4):

. (9.8)

Численно коэффициент теплопроводности равен количеству тепло­ты, проходящему в единицу времени через единицу изотермической поверхности при условии gradt=1. Его размерность Вт/(мК). Значе­ния коэффициента теплопроводности для различных веществ опреде­ляются из справочных таблиц, построенных на основании экспери­ментальных данных. Для большинства материалов зависимость коэф­фициента теплопроводности от температуры приближенно можно выразить в виде линейной функции

, (9.9)

где ₀ — значение коэффициента теплопроводности при температуре t₀=0 ⁰С; b — постоянная, определяемая опытным путем.

Наихудшими проводниками теплоты являются газы. Коэффициент теплопроводности газов возрастает с увеличением температуры и со­ставляет 0,0060,6 Вт/(мК). Следует отметить, что верхнее значение относится к гелию и водороду, коэффициент теплопроводности которых в 5—10 раз больше, чем у других газов. Коэффициент теплопроводности воздуха при 0 ⁰С равен 0,0244 Вт/(мК).

Для жидкости =0,070,7 Вт/(мК) и, как правило, умень­шается с увеличением температуры. Коэффициент теплопроводности воды с увеличением температуры возрастает до максимального значе­ния 0,7 Вт/(мК) при t=120 ⁰С и дальше уменьшается.

Наилучшими проводниками теплоты являются металлы, у которых =20418 Вт/(мК). Самый теплопроводный металл — серебро. Для большинства металлов коэффициент теплопроводности убывает с возрастанием температуры, а также при наличии разного рода при­месей. Поэтому коэффициент теплопроводности легированных сталей значительно ниже, чем чистого железа.

Материалы с 

9.4. Дифференциальное уравнение теплопроводности в плоской стенке при граничных условиях первого рода

9.4.1. Дифференциальное уравнение теплопроводности

Решение задач теплопроводности связано с определением поля тем­ператур и тепловых потоков. Для установления зависимости между величинами, характеризующими явление теплопроводности, восполь­зуемся методом математической физики, который рассматривает проте­кание физических процессов в произвольно выделенном из всего рассматриваемого пространства элементарном объеме и в течение беско­нечно малого промежутка времени. Это позволяет пренебречь изменением некото­рых величин и существенно упростить выкладки.

При выводе дифференциального урав­нения теплопроводности считаем, что те­ло однородно и изотропно (то есть физические свойства тела не зависят от выбранного в нём направления), физические параметры , с (теплоемкость), и  (плотность) постоянны, внутренние источники теплоты равномерно распределены в теле. Под внутренними источниками теплоты понимаются тепловыделения, например, в тепловыделяющих элементах атомных реакторов, или при прохожде­нии тока в электрических проводниках. Внутренние источники теплоты характеризуются величиной q_v — ко­личеством теплоты, которое выделяется в единице объема в единицу времени.

В основу вывода положен закон сохранения энергии, согласно которому вся теплота, выделенная внутренними источниками dQ_вн и внесенная извне в элементарный объем путем теплопроводности dQ_m за время d, идет на изменение внутренней энергии вещества, содержа­щегося в этом объеме:

. (9.10)

Выделим в теле элементарный параллелепипед с ребрами dx, dy, dz (рис. 9.1). Количество теплоты, которое проходит путем тепло­проводности внутрь выделенного объема в направлении оси Ох через элементарную площадку dydz за время d:

.

На противоположной грани параллелепипеда температура получит приращение и будет составлять .

Количество тепла, отведенного через эту грань:

.

Разница количества теплоты, подведенного к элементарному паралле­лепипеду и отведенного от него, представляет собой теплоту, внесен­ную путем теплопроводности в направлении оси Ох:

.

Аналогично:

;

Полное количество теплоты внесено в элементарный параллелепипед путем теплопроводности:

.

Здесь произведение dxdydz представляет собой объем элементарного параллелепипеда dv. Количество теплоты, которое выделилось в эле­ментарном объеме за счет внутренних источников:

.

Приращение внутренней энергии можно выразить через массу параллелепипеда dv, теплоемкость с и приращение температуры :

.

Подставляя выражения для dQ_m, dQ_вн и dU в уравнение (9.10), после соответствующих сокращений получаем:

. (9.11)

Сумма вторых частных производных любой функции в математи­ческом анализе носит название оператора Лапласа и обозначается следующим образом:

.

Величину называют коэффициентом температуропроводности и обозначают буквой a. В указанных обозначениях уравнение (9.11) примет вид:

. (9.12)

Это уравнение называется дифференциальным уравнением тепло­проводности или уравнением Фурье и лежит в основе математической теории теплопроводности. Коэффициент температуропроводности а является физическим параметром вещества. Из уравнения (9.12) следует, что изменение температуры во времени для любой точки тела пропорционально величине а.

9.4.2. Краевые условия

Дифференциальное уравнение (9.12) описывает в самом общем виде все без исключения задачи теплопроводности. Для решения конкретной задачи необходимо к диффе­ренциальному уравнению присоединить математическое описание частных ее особенностей. Эти дополнительные данные, которые ха­рактеризуют конкретное единичное явление, называются краевыми условиями, или условиями однозначности.

Существуют различные условия однозначности: геометрические — характеризующие форму и размеры тела, в котором протекает про­цесс теплопроводности; физические — характеризующие физические свойства тела; временные — характеризующие распределение темпера­туры тела в начальный момент времени; граничные — характеризую­щие взаимодействие тела с окружающей средой. Граничные условия в свою очередь бывают трех родов:

1) первого рода, задается распределение температуры на поверх­ности тела в функции времени;

2) второго рода, задается плотность теплового потока для всей поверхности тела в функции времени;

3) третьего рода, задаются температура окружающей среды t_ж и закон теплоотдачи между поверхностью тела и окружающей средой — закон Ньютона—Рихмана:

, (9.13)

где t_c — температура поверхности тела;  — коэффициент пропорцио­нальности, называемый коэффициентом теплоотдачи, Вт/(м²К). Коэф­фициент теплоотдачи численно равен количеству теплоты, отдаваемому или воспринимаемому единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой в один градус. Этот коэффициент учитывает все особенности явлении теплообмена, происходящие между поверхностью тела и окружающей средой. Плотность теплового потока, передаваемого от поверхности тела в окружающую среду,

. (9.14)

Согласно закону сохранения энергии, эта теплота равна теплоте, под­водимой к поверхности изнутри тела путем теплопроводности:

.

Переписав последнее уравнение в виде:

, (9.15)

получаем математическую формулировку граничных условий третьего рода. В результате решения дифференциального уравнения тепло­проводности совместно с условиями однозначности можно найти темпе­ратурное поле, а на основании закона Фурье — соответствующие тепловые потоки.

9.4.3. Теплопроводность через плоскую стенку при граничных условиях первого рода

Рассмотрим однородную плоскую стенку толщиной  (рис. 9.2). На наружных поверхностях стенки поддерживаются постоянные тем­пературы t_с1 и t_с2. Коэффициент теплопроводности стенки постоянен и равен . При стационарном режиме () и отсутствии внутренних источников теплоты (q_v=0) дифференциальное уравнение теплопро­водности примет вид:

. (9.16)

При заданных условиях температура будет изменяться только в на­правлении, перпендикулярном плоскости стенки (ось Оx). В этом случае

,

и дифференциальное уравнение теплопроводности перепишется в виде:

. (9.17)

Граничные условия первого рода запишутся следующим образом: при x=0 t=t_c1; при x= t=t_c2. Интегрируя уравнение (9.17), находим

.

После второго интегрирования получаем

. (9.18)

Постоянные С₁ и С₂ определим из граничных условий: при x=0 t=t_c1, С₂= t_c1; при x= t=t_c2= С₁+t_c1, отсюда . Подставляя значения С₁ и С₂ в уравнение (9.18), получим уравнение распределения температуры по толщине стенки:

. (9.19)

Для определения плотности теплового потока, проходящего через стенку в направлении оси Оx, воспользуемся законом Фурье, согласно которому .

Учитывая, что , получим

. (9.20)

Общее количество теплоты, которое передается через поверхность стенки F за время ,

. (9.21)

Отношение называют тепловой проводимостью стенки, обратную ей величину – термическим сопротивлением теплопровод­ности. Поскольку величина  зависит от температуры, в уравнения (9.20), (9.21) необходимо подставить коэффициент теплопровод­ности _с, взятый при средней температуре стенки.

zavantag.com

Реферат Теплопроводность

скачать

Реферат на тему:

План:

Введение

• 1 Закон теплопроводности Фурье
  • 1.1 Коэффициент теплопроводности вакуума
  • 1.2 Связь с электропроводностью
• 2 Обобщения закона Фурье
• 3 Коэффициенты теплопроводности различных веществ
Примечания

Введение

Не следует путать с термическим сопротивлением.

Теплопрово́дность — это перенос тепловой энергии структурными частицами вещества (молекулами, атомами, ионами) в процессе их теплового движения. Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. Явление теплопроводности заключается в том, что кинетическая энергия атомов и молекул, которая определяет температуру тела, передаётся другому телу при их взаимодействии или передаётся из более нагретых областей тела к менее нагретым областям. Иногда теплопроводностью называется также количественная оценка способности конкретного вещества проводить тепло.

Численная характеристика теплопроводности материала равна количеству теплоты, проходящей через материал толщиной 1 м и площадью 1 кв.м за единицу времени (секунду) при разности температур на двух противоположных поверхностях в 1 К. Данная численная характеристика используется для расчета теплопроводности для калибрования и охлаждения профильных изделий.

Исторически считалось, что передача тепловой энергии связана с перетеканием теплорода от одного тела к другому. Однако более поздние опыты, в частности, нагрев пушечных стволов при сверлении, опровергли реальность существования теплорода как самостоятельного вида материи. Соответственно, в настоящее время считается, что явление теплопроводности обусловлено стремлением занять состояние более близкое к термодинамическому равновесию, что выражается в выравнивании температуры.

1. Закон теплопроводности Фурье

В установившемся режиме поток энергии, передающейся посредством теплопроводности, пропорционален градиенту температуры:

где  — вектор потока тепла — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси,  — коэффициент теплопроводности (иногда называемый просто теплопроводностью), T — температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad T (то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье.

В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):

где P — полная мощность тепловых потерь, S — площадь сечения параллелепипеда, ΔT — перепад температур граней, h — длина параллелепипеда, то есть расстояние между гранями.

Коэффициент теплопроводности измеряется в Вт/(м·K).

1.1. Коэффициент теплопроводности вакуума

Коэффициент теплопроводности вакуума почти ноль (чем глубже вакуум, тем ближе к нулю). Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тем не менее, тепло в вакууме передаётся с помощью излучения. Поэтому, например, для уменьшения теплопотери стенки термоса делают двойными, серебрят (такая поверхность лучше отражает излучение), а воздух между ними откачивают.

1.2. Связь с электропроводностью

Связь коэффициента теплопроводности K с удельной электрической проводимостью σ в металлах устанавливает закон Видемана — Франца:

где k — постоянная Больцмана, e — заряд электрона.

2. Обобщения закона Фурье

Следует отметить, что закон Фурье не учитывает инерционность процесса теплопроводности, то есть в данной модели изменение температуры в какой-то точке мгновенно распространяется на всё тело. Закон Фурье не применим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т. д. Инерционность в уравнения переноса первым ввел Максвелл^[1], а в 1948 году Каттанео был предложен вариант закона Фурье с релаксационным членом:^[2]

Если время релаксации τ пренебрежимо мало, то это уравнение переходит в закон Фурье.

3. Коэффициенты теплопроводности различных веществ

Цветок на куске аэрогеля над горелкой Бунзена

Материал	Теплопроводность, Вт/(м·K)
Графен	(4840±440) — (5300±480)
Алмаз	1001—2600
Серебро	430
Медь	382—390
Золото	320
Алюминий	202—236
Латунь	97—111
Железо	92
Платина	70
Олово	67
Сталь	47
Кварц	8
Стекло	1-1,15
КПТ-8	0,7
Вода при нормальных условиях	0,6
Кирпич строительный	0,2—0,7
Пенобетон	0,14—0,3
Дерево	0,15
Свежий снег	0,10—0,15
Вата	0,055
Воздух (300 K, 100 кПа)	0,026
Вакуум (абсолютный)	0 (строго)

другие вещества

Материал	Теплопроводность, Вт/(м·K)
Кальций	201
Бериллий	201
Вольфрам	173
Магний	156
Родий	150
Иридий	147
Молибден	138
Рутений	117
Хром	93,9
Осмий	87,6
Титан	21,9
Тефлон	0,25
Бумага	0,14
Полистирол	0,082
Шерсть	0,05
Минеральная вата	0,045
Пенополистирол	0,04
Стекловолокно	0,036
Пробковое дерево	0,035
Пеноизол	0,035
Каучук вспененный	0,03
Аргон	0,0177
Аэрогель	0,017
Ксенон	0,0057

На практике нужно также учитывать проводимость тепла за счет конвекции молекул и проникаемости излучений. Например, при полной нетеплопроводности вакуума, тепло может передаваться за счет излучения (пример — Солнце, установки инфракрасного излучения). А газ или жидкость могут обмениваться нагретыми или охлажденными слоями самостоятельно или искусственно (пример — фен, греющие вентиляторы).

Примечания

1. J. C. Maxwell, Philos. Trans. Roy. Soc. London 157 (1867) 49.
2. C. Cattaneo, Atti Seminario Univ. Modena 3 (1948) 33.

wreferat.baza-referat.ru