Теплопроводность тема: Теплопередача — урок. Физика, 8 класс.

Виды теплопередачи. Теплопроводность. Конвекция. Излучение.

Урок 3. Тема: Виды теплопередачи. Теплопроводность. Конвекция. Излучение.

Примеры теплопередачи в природе и технике.

Цели: Познакомить учащихся с видами теплопередачи и привести примеры теплопередачи в природе и технике

Задачи:

– Образовательная: раскрыть понятия теплопроводность, конвекция, излучение. Познакомить с примерами теплопередачи в природе и технике.

– Развивающая: развивать внимание, воображение и память.

– Воспитательная: воспитывать самостоятельность, любовь к предмету.

Структура урока:

1. Организационный момент.

2. Проверка домашнего задания. (индивидуальные карточки).

3. Актуализация знаний. Объяснение нового материала .

4. Закрепление нового материала .

5. Домашнее задание.

6. Подведение итогов.

7. Рефлексия.

Ход урока.

1. Организационный момент. Приветствие. Выявление отсутствующих. Проверка готовности к уроку.

2. Проверка домашнего задания. Вопросы в конце параграфов 1-3.Карточки. в Приложении 1.

Вопросы:

1. Какие тепловые явления вы знаете? Что характеризует температура? Как связана температура тела со скоростью его молекул? Чем отличается движение молекул в газах, жидкостях и твердых телах?

2. Какие превращения энергии происходят при подъеме шара и при его падении? Как изменяется состояние свинцового шара и свинцовой плиты в результате их соударения? Какую энергию называют внутренней энергией тела? Зависит ли внутренняя энергия тела от его движения и положения относительно других тел?

Проверка упр. 1 №1 и2 стр. 8.

3. Пользуясь рисунком 3, расскажите, как изменяется внутренняя энергия тела, когда над ним совершают работу. Опишите опыт, показывающий, что за счет внутренней энергии тело может совершить работу.

4. Объясните на основе молекулярного строения вещества нагревание спицы, опущенной в горячую воду.

5. Что такое теплопередача? Какими двумя способами можно изменить внутреннюю энергию.

3. Актуализация знаний. Объяснение нового материала.

Вспомним что называется теплопередачей? (Из прошлого урока вам известно, что процесс изменения внутренней энергии при теплообмене без совершения работы над телом или самим телом называется теплопередачей.)

Запишем тему урока. ( Слайд 1).

Частицы более нагретого тела, имея большую кинетическую энергию, при контакте с менее нагретым телом передают энергию непосредственно частицам менее нагретого тела.

Существуют 3 вида теплопередачи: теплопроводность, конвекция и излучение. ( Слайд 2).

1) Рассмотрим 1 вид теплопередачи, теплопроводность. Запишем определение для теплопроводности. 

Явление передачи энергии от более нагретой части тела к менее нагретой или от более нагретого тела к менее нагретому через непосредственный контакт или промежуточные тела. В различных веществах(твердых, жидких, газообразных) она различна. Рассмотрим примеры на слайдах 2-7.

Прочитать два последних абзаца из параграфа 4 на странице 13 и ответить на вопрос.

Почему мех, пух, перья на теле животных и птиц, а также одежда человека защищают от холода? (слайд 8)

Ответим на вопросы: (слайд 9).

1. В стакан налит горячий чай. Как осуществляется теплообмен между чаем и стенками стакана?

2. Почему нагретые детали охлаждаются в воде быстрее, чем на воздухе?

3. Зачем ствол винтовки покрывают деревянной накладкой?

4. Почему вы обжигаете губы, когда пьете чай из металлической кружки, и не обжигаете, когда пьете чай из фарфоровой кружки? (Температура чая одинаковая.)

5. Если температура в комнате 16 °С, то нам не холодно, но если войти в воду, температура которой 20 °С, то мы ощущаем довольно сильный холод. Почему?

2) Еще один вид теплопередачи это конвекция. (слайд 11)

Конвекция – это процесс теплопередачи, при котором энергия переносится струями жидкости или газа. Она отсутствует в твердых телах и не имеет места в вакууме. 

Различают два вида конвекции: естественную ( или свободную) и вынужденную.

3) Излучение. Процесс передачи энергии от одного тела к другому с помощью электромагнитных волн. Интенсивность излучения зависит от температуры, чем выше температура тела, тем больше излучение.

В каких средах происходит излучение? Привести примеры. Происходит во всех средах.

1. 4. Закрепление материала.

      1. Теплопередача это?

      2. Виды теплопередач?

      3. Примеры теплопроводности.

      4. Объяснить процесс конвекция и излучения

      5. Примеры теплопередачи в природе и технике.

   5. Д/з параграф 4-6, упражнения в конце параграфов ( устно). Доклады или презентации по темам: «Устройство термоса», и «Теплопередача и растительный мир».

   6. Подведение итогов. Выставление оценок за работу на уроке.

   7. Рефлексия. Что нового, вы узнали сегодня на уроке? Какие были трудности? Удалось ли их преодолеть? Пригодятся ли вам знания, полученные сегодня на уроке

Резервное время. Самостоятельно ответим на вопросы. ( слайд 10 )

1. Какое из перечисленных ниже веществ имеет наибольшую теплопроводность?

А. Мех. Б. Дерево. В. Сталь.

1. Какое из перечисленных ниже веществ имеет наименьшую теплопроводность?

А. Воздух. Б. Чугун. В. Алюминий.

2. Какое из перечисленных ниже веществ имеет наименьшую теплопроводность?

А. Опилки. Б. Свинец. В. Медь.

2. Какое из перечисленных ниже веществ имеет наибольшую теплопроводность?

А. Солома. Б. Вата. В. Железо.

3.В каком доме теплее зимой при одинаковой толщине стен: деревянном или кирпичном?

3. В какой одежде человеку теплее: хлопчатобумажной или шерстяной?

Приложение 1.

СР-1 Тема: Тепловое движение. Температура.

Вариант 1.

1. Какие явления называются тепловыми?

2. Какие из перечисленных ниже явлений относятся к тепловым явлениям:

а) таяние снега под лучами солнца;

б) движение автомобиля по дороге;

в) нагревание воды в электрическом чайнике;

г) появление радуги на небе?

3. Имеется три сосуда с холодной, теплой и горячей водой. Сравните скорости движения молекул воды в этих сосудах.

СР-1 Тема: Тепловое движение. Температура.

Вариант 2.

1. Какое из перечисленных ниже движений является тепловым:

а) движение Луны вокруг Земли;

б) беспорядочное движение молекул тела;

в) движение фигуриста на льду;

г) полет воздушного шара?

2. Как изменяется скорость движения молекул при повышении температуры?

3. Имеется два сосуда с водой. В одном сосуде температура воды 20 С, в другом – 100 С. В каком сосуде средняя кинетическая энергия молекул воды больше?

СР-1 Тема: Тепловое движение. Температура.

Вариант 1.

1. Какие явления называются тепловыми?

2. Какие из перечисленных ниже явлений относятся к тепловым явлениям:

а) таяние снега под лучами солнца;

б) движение автомобиля по дороге;

в) нагревание воды в электрическом чайнике;

г) появление радуги на небе?

3. Имеется три сосуда с холодной, теплой и горячей водой. Сравните скорости движения молекул воды в этих сосудах.

СР-1 Тема: Тепловое движение. Температура.

Вариант 2.

1. Какое из перечисленных ниже движений является тепловым:

а) движение Луны вокруг Земли;

б) беспорядочное движение молекул тела;

в) движение фигуриста на льду;

г) полет воздушного шара?

2. Как изменяется скорость движения молекул при повышении температуры?

3. Имеется два сосуда с водой. В одном сосуде температура воды 20 С, в другом – 100 С. В каком сосуде средняя кинетическая энергия молекул воды больше?

Теплопроводность. Передача теплоты от одних частей тела к другим. Методические материалы

Цифровой ресурс может использоваться для обучения в рамках программы основной и средней школы (базового уровня).

Компьютерная модель представляет собой иллюстрацию явления передачи теплоты от одних частей тела к другим на примере опытов, в которых нагреву подвергаются стержни из различных металлов.

Краткая теория

Различные вещества имеют разную теплопроводность.

Теплопроводность – это один из видов теплообмена, при котором происходит непосредственная передача энергии от частиц более нагретой части тела к частицам его менее нагретой части. При теплопроводности само вещество не перемещается вдоль тела, происходит лишь перенос энергии.

Работа с моделью

Демонстрация состоит из трех экранов. Нагреваются стержни из различных по теплопроводности металлов, к которым прикреплены кнопки с помощью пластилина. По мере нагрева пластилин плавится и кнопки падают на подставку. Модель может быть использована в режиме ручного переключения кадров и в режиме автоматической демонстрации (). Пользователь может приостановить или возобновить демонстрацию процесса с помощью кнопки .

Рекомендации по применению модели

Данная модель может быть применена в качестве иллюстрации на уроках изучения нового материала в 8 классе по теме «Теплопроводность». На примере этой модели можно рассмотреть с учащимися процесс передачи энергии от более нагретой части тела к менее нагретой, зависимость теплопроводности тел от вещества.

Пример планирования урока с использованием модели

Тема «Теплопроводность»

Цель урока: рассмотреть такой вид теплопередачи как теплопроводность; установить зависимость теплопроводности разных тел от вещества, агрегатного состояния, дать этому объяснение с точки зрения строения вещества; обсудить применение разной теплопроводности тел в быту и технике.

№ п/п Этапы урока Время, мин Приемы и методы 1 Организационный момент 2 2 Проверка домашнего задания по теме «Способы изменения внутренней энергии» 5 Тест 3 Объяснение нового материала с использованием компьютерных моделей «Передача теплоты от одних частей тела к другим», «Явление теплопроводности». 20 Объяснение нового материала с применением компьютерных моделей «Передача теплоты от одних частей тела к другим», «Явление теплопроводности» 4 Решение качественных задач 10 Фронтальная работа 5 Объяснение домашнего задания 3

Таблица 1.

Примеры вопросов и заданий

Сковорода стоит на горячей плите. Каким способом происходит в основном теплопередача от нижней стороны сковороды к верхней ее стороне?

Урок 02. теплопроводность. конвекция. излучение – Физика – 8 класс

Конспект объясняющего модуля

Цели урока:

– познакомить с тремя способами теплопередачи, сформировать представление о механизмах и особенностях передачи энергии путём теплопроводности, конвекции и излучения;

– научить наблюдать, описывать и объяснять физические явления на основе представлений об изменении внутренней энергии при теплопередаче.

Планируемые результаты обучения учащегося:

– даёт определения теплопроводности, конвекции и излучения, приводит примеры передачи энергии перечисленными способами;

– демонстрирует знание механизмов и особенностей передачи энергии путём теплопроводности, конвекции и излучения;

– сравнивает значения теплопроводности различных веществ;

– приводит примеры и объясняет физические явления на основе полученных знаний о различных способах теплопередачи.

В окружающем нас мире происходят различные физические явления, некоторые из них связаны с изменением внутренней энергии тел.

Внутреннюю энергию можно изменить за счет совершения механической работы и теплопередачи.

Рассмотрим способ изменения внутренней энергии тела путем теплопередачи. Введем определение. Теплопередача – это процесс изменения внутренней энергии без совершения работы над телом или самим телом.

У теплопередачи есть три разновидности: теплопроводность, конвекция, излучение. Каждый вид теплопередачи имеет свои особенности, присущие только ему. Рассмотрим первый вид- теплопроводность.

Теплопроводность – это явление, при котором энергия передаётся от одной части тела к другой посредством движения частиц или при непосредственном контакте двух тел.

Разные тела обладают разной теплопроводностью, так как молекулярное строение и скорость движения молекул в разных веществах разная.

У металлов самая высокая (хорошая) теплопроводность, у жидкостей меньше, а у газов самая маленькая ( плохая) теплопроводность.

Важно отметить, что при теплопроводности не происходит переноса вещества и если нет частиц, то нет теплопроводности. Следующий вид теплопередачи- конвекция.

Конвекция – это явление переноса энергии слоями жидкостей или газов.

Конвекция , что следует из определения, может быть только при наличии вещества, а конкретно – жидкости или газа, если же вещества нет, то и не имеет смысла говорить о явлении конвекции. Конвекцией, например, объясняются бризы – ночные и дневные ветры, возникающие на берегах морей и больших озер.

В летние дни суша прогревается солнцем быстрее, чем вода, поэтому и воздух над сушей нагревается больше, чем над водой. При этом воздух над сушей расширяется, после чего его давление становится меньше давления более холодного воздуха над морем. В результате холодный воздух понизу с моря (где давление больше) перемещается к берегу (где давление меньше) -дует ветер. Это и есть дневной (или морской) бриз.

Ночью вода охлаждается медленнее, чем суша, и над сушей воздух становится более холодным, чем над водой. Теперь более высокое давление оказывается над сушей, и потому воздух начинает перемещаться от берега к морю. Это ночной (или береговой) бриз.

Различают два вида конвекции: естественная и вынужденная.

Естественная конвекция происходит сама по себе без внешнего воздействия.

В вынужденной перемещение вещества обусловлено действием внешних сил (насос, лопасти вентилятора и т. п.). Рассмотрим еще один вид теплопередачи- излучение, который может осуществляться в вакууме.

Под излучением, понимают перенос энергии в виде электромагнитных волн.

У излучения есть свои особенности- темные тела быстрее поглощают и излучают энергию, у светлых поглощение и испускание энергии происходит гораздо медленнее.

Кроме того, все нагретые тела, по сравнению с температурой окружающего пространства, испускают энергию. Чем сильнее нагрето тело, тем больше энергии оно испускает.

Это можно увидеть с помощью термоскопа.

Подборка опытов к теме «Виды теплопередачи» (УМК любой, ФГОС)

Опыты по теме «Виды теплопередачи»

1. Возьмите учебные весы и уравновесьте их. Поднесите горящую спичку под чашку весов снизу на расстоянии 10—12 см.
Почему они выходят из равновесия?
Оказывается, при горении спички возникают восходящие конвекционные потоки, которые вызывают подъем чашки.

2. Как можно нарушить равновесие учебных весов с помощью горящей свечи и с помощью льда, не прикасаясь к чашам весов? Объяснить получившийся результат.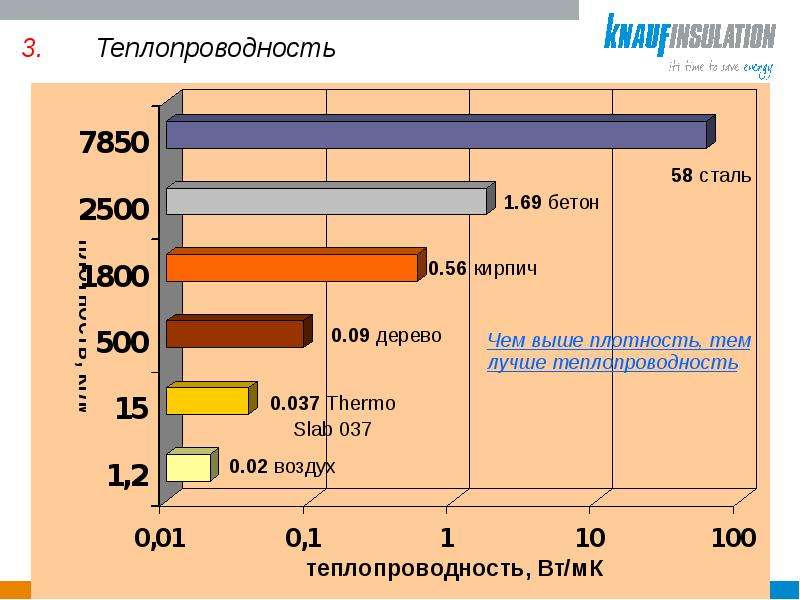 Какой вид теплопередачи используется?

 Решение: горящую свечу надо подержать под чашей весов, а лед – над  чашей. Теплый воздух над свечой, расширяясь, поднимается вверх и нарушает равновесие весов. Холодный воздух тяжелее теплого и опускается вниз, нарушая равновесие весов. Вид теплопередачи – конвекция.

3. Фронтальный опыт «Виды теплопередачи»

Оборудование : стакан с горячей водой, термометр.

Ход опыта: 

а) Измеряют температуру воздуха в непосредственной близости обоснования стакана, сбоку и дают ответ на вопрос: «Какой вид теплопередачи имеет место при таком измерении»?

Ответ: Излучение, т.к. между термометром и стаканом имеется воздух, обладающий плохой теплопроводностью, и теплопроводности быть не может. Конвекция же происходит снизу вверх.

б) температуру воздуха над стаканом, на расстоянии около 5 см. дают обоснованный ответ на вопрос: «Какой вид теплопередачи имеет место в данном случае»?

Ответ: Конвекция, т.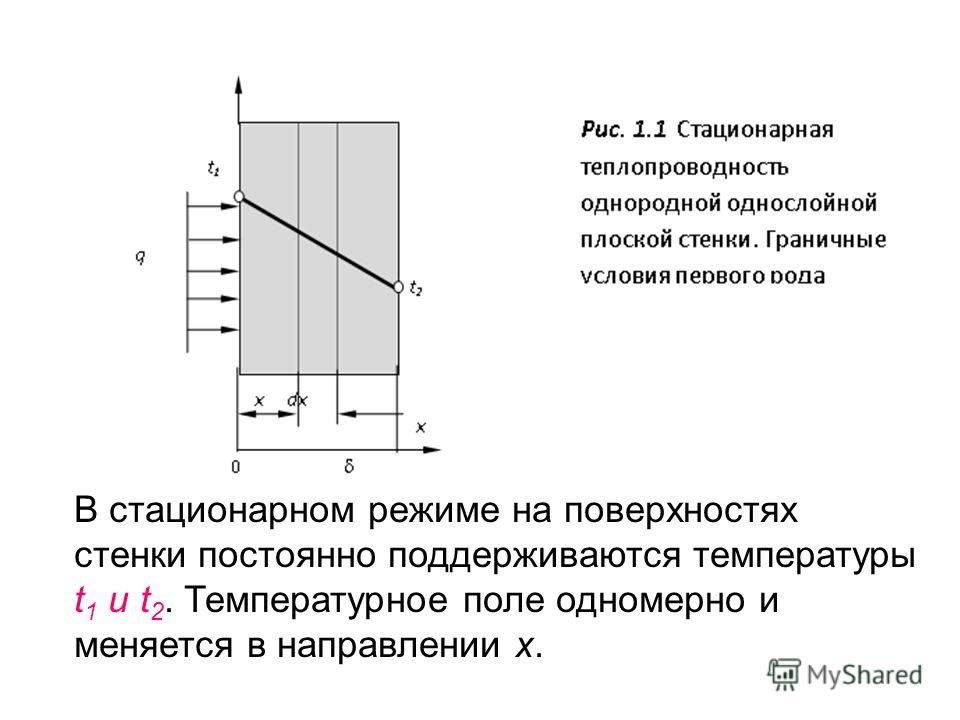 к. тепло от горячей воды передается потоками воздуха снизу вверх.

в) измеряют температуру воды в стакане и дают ответ на вопрос: «Какой вид теплопередачи имеет место в данном случае»?

Ответ: Теплопроводность, т.к. теплопередача происходит при непосредственном контакте.

4. Конвекция в жидкостях. На столе два стакана с горячей водой, один стоит на льду, а на крышке другого лежит лед. Учащиеся объясняют, в каком стакане вода остынет быстрее.

5. Греет ли шуба?

Нам понадобятся:

Кусочки льда, шуба (или другая теплая одежда), фольга, полиэтиленовый пакет, бумага, ткань.

Ход эксперимента:

Если льдинку положить в шубу, она растает быстрее? Попробуйте, и убедитесь сами: возьмите два кусочка льда, положите их в пластиковые пакеты (чтобы тающая вода не замочила шубу). Один из них заверните в шубу, другой оставьте лежать на открытом воздухе (это будет контрольный экземпляр). И наблюдайте, что с ними происходит. Когда лед на открытом воздухе уже заметно подтает, разверните шубу – вы увидите, что льдинка в ней тает гораздо медленнее. У нас льдинка на воздухе растаяла полностью  за полчаса, а льдинка, “одетая в шубу”, сохранялась в течение 3 часов!

Опыт можно продолжить: заверните лед в разные материалы (полиэтилен, газету, фольгу, ткань) и проверьте – в каких лед тает быстрее, а в каких медленнее. Сделайте выводы о теплопроводности этих материалов.

 Здесь можно найти еще 9 опытов со льдом и водой http://www.tavika.ru/2013/12/ice-experiment-part-1.html

Детские, но очень познавательные!

6. Тяга. Зажгите стеариновую свечу, накройте ее стеклянной цилиндрической трубкой. При этом пламя уменьшается и может погаснуть. Почему?

Если трубку приподнять, то свеча горит ярче. Почему?
Когда горящую свечу накрывают стеклянной цилиндрической трубкой, доступ кислорода к свече ухудшается и ее пламя уменьшается.

При подъеме трубки улучшается доступ кислорода к горящей свече, улучшается тяга.

Еще несколько опытов на конвекцию http://class- fizika.spb.ru/index.php/opit/678-op-konv

7. Де­мон­стра­ция яв­ле­ния кон­век­ции в воз­ду­хе. Для на­гляд­но­го на­блю­де­ния кон­век­ции в воз­ду­хе возь­мем све­тиль­ник из 4 све­чей и кры­лат­ки, ко­то­рая может сво­бод­но вра­щать­ся, рас­по­ло­жен­ной ввер­ху. За­жжем все свечи и сразу же по­лу­чим воз­мож­ность на­блю­дать вра­ще­ние уста­нов­лен­ной на све­тиль­ник кры­лат­ки. По­че­му так про­ис­хо­дит? Воз­дух на­гре­ва­ет­ся пла­ме­нем каж­дой свечи и рас­ши­ря­ет­ся, вслед­ствие этого умень­ша­ет­ся его плот­ность, и по за­ко­ну Ар­хи­ме­да он на­чи­на­ет под­ни­мать­ся вверх и вра­щать вер­туш­ку. При этом, хо­лод­ный воз­дух, рас­по­ло­жен­ный во­круг, опус­ка­ет­ся, за­ни­мая место на­гре­то­го, на­гре­ва­ет­ся сам и под­ни­ма­ет­ся, об­ра­зуя так на­зы­ва­е­мые кон­век­тив­ные по­то­ки. Таким об­ра­зом, мы можем на­блю­дать яв­ле­ние кон­век­ции в воз­ду­хе для ис­сле­ду­е­мо­го све­тиль­ни­ка.

Ин­те­рес­но то, что при ту­ше­нии све­чек по оче­ре­ди, ско­рость вра­ще­ния кры­лат­ки по­сте­пен­но умень­ша­ет­ся, т. к. умень­ша­ет­ся объем цир­ку­ли­ру­ю­ще­го воз­ду­ха, и мы можем на­блю­дать, что яв­ле­ние кон­век­ции может быть раз­лич­ным по своей эф­фек­тив­но­сти в за­ви­си­мо­сти от усло­вий про­ве­де­ния опыта.

Ана­ло­гич­но более про­стой экс­пе­ри­мент можно про­ве­сти и прак­ти­че­ски без до­пол­ни­тель­но­го обо­ру­до­ва­ния, имея толь­ко ка­ран­даш и вы­ре­зан­ные бу­маж­ные ло­па­сти (см. рис.).

8.

Методическая разработка урока по теме «Теплопроводность».

Методическая разработка урока по теме «Теплопроводность». Класс: 8 Учебник: Физика. 8 кл.:учеб. для общеобразоват. учреждений /  А.В.Перышкин. – М.:Дрофа, 2013. – 237.  Тема урока: Теплопроводность Тема предыдущего урока: Способы изменения внутренней энергии тела. Тема следующего урока: Конвекция. Цели урока:  Образовательные: сформировать знания обучающихся о теплопроводности;  сформулировать определение понятия теплопроводность; выяснить как  происходит передача энергии по металлической проволоке; выяснить какие из веществ обладают большей, а какие меньшей теплопроводностью; объяснить  почему пух, мех и перья обладают плохой теплопроводностью; объяснить  практическое применение полученных знаний (теплопроводность в жизни). Развивающие: развитие памяти, логического мышления, умения сравнивать,  обобщать, самостоятельно делать выводы; развитие речевой деятельности;  умений работать самостоятельно Воспитательные: воспитывать аккуратность и точность при выполнении  заданий; самостоятельность и самоконтроль; формирование культуры  учебного труда; продолжить формирование устойчивого познавательного  интереса к предмету.  Тип урока: комбинированный Оборудование: компьютер, мультимедийный проектор, интерактивная доска,  презентация (приложение на диске). Оборудование для проведения опытов: пробирки, спиртовка, штатив,  проволока, спички, пластилин, лед Структура урока: I. Актуализация знаний. 1. Мобилизующее начало урока (30 сек) 2. Индивидуальный опрос с целью проверки домашнего задания (5 мин) 3. Выполнение теста с целью определения уровня усвоения темы (7 мин) 4. Постановка проблемы, с целью проведения мотивации к изучению  новой темы (1 мин 30 сек) Формирование новых знаний и способов действий II. 1. Эвристическая беседа с целью формулировки определения понятия  теплопроводности;(5 мин)  2. Проведение опытов с целью выяснения особенностей явления  теплопроводности в твердых телах (6 мин)  3. Физкультминутка (1 мин) 4. Проведение опытов с целью выяснения особенностей явления  теплопроводности в жидкостях, газах; (5 мин) 5. Рассказ учителя с целью выяснения особенностей явления  теплопроводности в вакууме (2 мин) 6. Постановка целей на следующий этап урока (1 мин) III. Формирование умений и навыков 1. Выполнение упражнения с целью применения знаний, полученных на  уроке (5 мин) 2. Постановка домашнего задания (2 мин) 3. Подведение итогов урока (4мин) Описание хода проведения урока  (в приложение – технологическая карта урока, даны примерные ответы  обучающихся) I. Актуализация знаний. 1.Мобилизующее начало урока (30 сек) Приветствие класса. Проверка готовности обучающихся к занятию. 2. Индивидуальный опрос с целью проверки домашнего задания (5 мин) ­ Давайте вспомним что мы с вами изучали на прошлом уроке? ­ Что такое внутренняя энергия? ­ От чего зависит внутренняя энергия? От чего она не зависит?  ­ Внутренняя энергия тела — это величина постоянная? ­ Каким образом можно изменить внутреннюю энергию?  ­ Какими способами можно изменить скорость движения молекул? ­ Опишите опыт, показывающий, что внутренняя энергия увеличивается.  ­ Пример опыта, подтверждающего   уменьшение внутренней энергии? ­ Какими еще способами можно изменить внутреннюю энергию тела? ­ Что такое теплопередача?  ­ Что мы ещё узнали о теплопередаче?  3. Выполнение теста с целью определения уровня усвоения темы (8 мин) После того, как мы повторили с вами теоретический материал, я хочу вам  предложить выполнить тест по теме «Внутренняя энергия и способы её  изменения».  Обучающиеся берут нетбуки (ими оснащен кабинет физики) и  приступают к выполнению теста. Тест (№6) выполняет в интерактивном  приложении к учебнику (Физика.8 класс. Дрофа) Время выполнения теста – 6 мин. Критерии оценивания теста. 6 правильных ответов –  отметка «5», 5  правильных ответов – отметка «4», 4 правильных ответа – отметка «3».  Отметки за тест учащиеся выставляют себе в оценочных листах.  4.Постановка проблемы, с целью проведения мотивации к изучению новой  темы (1 мин 30 сек) Как вы думаете, чем мы займемся сегодня на уроке? Что мы будем изучать? Вы правы, мы перейдем к изучению способов теплопередачи, а именно мы  познакомимся с теплопроводностью.  Какая тема сегодняшнего урока? Что мы должны будем сделать на уроке, какие цели нашего урока? II. Формирование новых знаний и способов действий 1.Эвристическая беседа с целью формулировки определения понятия  теплопроводности;(5 мин)  Запишите тему урока «Теплопроводность». Давайте вспомним, на прошлом уроке мы с вами рассмотрели опыт.  При  опускании металлической спицы в стакан с горячей воды очень скоро конец  спицы становится тоже горячим.  О чем свидетельствует этот опыт? Приведите ещё один пример, при котором внутренняя энергия передается от  одной части тела к другой.  Явление, которое рассмотрено в этих опытах и есть теплопроводность.  Давайте попробуем сформулировать определение теплопроводности.  Вы правы. Давайте запишем определение. Теплопроводность – явление  передачи внутренней энергии от одного тела к другому или от одной его  части к другой. 2.Проведение опытов с целью выяснения особенностей явления  теплопроводности в твердых телах (6 мин)  Запишите тему урока «Теплопроводность». Давайте вспомним, на прошлом уроке мы с вами рассмотрели опыт. При  опускании металлической спицы в стакан горячей воды очень скоро конец  спицы становится тоже горячим.  О чем свидетельствует этот опыт? Приведите ещё один пример, при котором внутренняя энергия передается от  одной части тела к другой.  Явление, которое рассмотрено в этих опытах и есть теплопроводность.   Давайте попробуем сформулировать определение теплопроводности.  Вы правы. Давайте запишем определение. Теплопроводность – явление  передачи внутренней энергии от одного тела к другому или от одной его  части к другой. Давайте теперь рассмотрим и проведем ряд опытов.  1)Стеклянную палочку держим над пламенем спиртовки.  Что произойдет?  (проводит обучающийся) 2) Если таким же образом нагреть металлический стержень. Быстрее он  нагреется или нет? 3) Возьмем три различные металлических спицы. К спицам прикрепим на  пластилине спички. Начнем нагревать конец спиц, что мы наблюдаем.  Почему спички начали падать? (опыт помогает проводить обучающийся) Если мы держим над пламенем спиртовки деревянную и стеклянную палочку,  металлическую спицу.  Наша рука почувствует, что спица или палочка  нагрелись одновременно или нет? Это значит, что дерево и стекло обладают плохой теплопроводностью.  А  металл обладает хорошей теплопроводностью.  Самая большая  теплопроводность у серебра и меди.  Разберемся теперь как происходит передача энергии по проволоке? В той  части проволоки, которая ближе к спиртовке, скорость колебательного  движения частиц металла увеличивается.  Частицы постоянно  взаимодействуют друг с другом, увеличивается скорость движения соседних  частиц.  Постепенно растет температура следующей части проволоки и т.д.  При теплопроводности не происходит перенос вещества от одного конца тела  к другому.  3.Физкультминутка (1 мин) Отложите ручки в сторону, положите руки на парту. Поверните голову  вправо, влево, повторите упражнение 10 раз. Наклоните голову вперед, назад,  повторите 10 раз. 4.Проведение опытов с целью выяснения особенностей явления  теплопроводности в жидкостях, газах; (5 мин) Давайте теперь рассмотрим, как происходит теплопроводность жидкостей. Пробирка с водой.  Положим в неё кусочек льда. Начнем нагревать верхнюю  часть пробирки. (опыт помогает проводить обучающийся) Что мы наблюдаем? Если лед не растаял, о чем это свидетельствует? Правильно, вода обладает плохой теплопроводностью.  Следовательно, и  жидкости обладают плохой теплопроводностью, за исключением ртути и  расплавленных металлов. Связано это с тем, что в жидкостях молекулы расположены на больших  расстояниях друг от друга, чем в твердых телах.    Мы с вами рассмотрели теплопроводность твердых тел и жидкостей. Что ещё  нам осталось сделать?  5)Сухую пробирку надеваем на палец и нагреваем в пламени спиртовки  донышком вверх. Палец не чувствует тепла.  О чем свидетельствует данный опыт? С чем это связано?  5.Рассказ учителя с целью выяснения особенностей явления  теплопроводности в вакууме (2 мин) Давайте теперь рассмотрим, как происходит теплопроводность жидкостей. Пробирка с водой.  Положим в неё кусочек льда. Начнем нагревать верхнюю  часть пробирки.  Что мы наблюдаем? Если лед не растаял, о чем это свидетельствует?  Правильно, вода обладает плохой теплопроводностью.  Следовательно, и  жидкости обладают плохой теплопроводностью, за исключением ртути и  расплавленных металлов. Связано это с тем, что в жидкостях молекулы расположены на больших  расстояниях друг от друга, чем в твердых телах.   Мы с вами рассмотрели теплопроводность твердых тел и жидкостей. Что ещё  нам осталось сделать?  5)Сухую пробирку надеваем на палец и нагреваем в пламени спиртовки  донышком вверх.  Палец не чувствует тепла.  О чем свидетельствует данный опыт? С чем это связано? У разных веществ теплопроводность различна.  Плохой теплопроводностью обладают шерсть, волосы, перья птиц, бумага,  пробка и другие пористые тела. Связано это с тем, что между волокнами этих  веществ содержится воздух.  Самой низкой теплопроводностью обладает вакуум. Связано это с тем, что  теплопроводность – перенос энергии от одной части тела к другой, который  происходит при взаимодействии молекул или других частиц.  В пространстве,  где нет частиц, теплопроводность осуществляться не может.  Чтобы предохранить тело от охлаждения или нагревания, необходимо  применять вещества с малой теплопроводностью.  Например, для кастрюль и сковородок ручки изготавливают из пластмассы.  Дома строят из бревен или кирпича, так как они обладают плохой  теплопроводностью, следовательно, предохраняют помещение от охлаждения 6.Постановка целей на следующий этап урока (1 мин) Мы с вами сегодня хорошо поработали, изучили явление теплопроводности.   Что нам еще осталось сделать?  Вы правы, давайте попробуем применить полученные сегодня знания. III.Формирование умений и навыков 1.Выполнение упражнения с целью применения знаний, полученных на уроке  (5 мин) Откройте свои учебники на странице 14. Давайте выполним упражнение 3.  Прочитайте первое задание.  Почему глубокий рыхлый снег предохраняет озимые хлеба от вымерзания? Теплопроводность сосновых досок в 3,7 раза больше, чем сосновых опилок.   Чем объясняется эта разница?  Почему вода не замерзает под толстым слоем льда?  Почему шуба не греет?  2.Постановка домашнего задания (2мин) Откройте дневники запишите домашнее задание: п.4, ответить на вопросы  устно, задание после параграфа. Рабочая тетрадь – задание 4,2;4,3 Подготовить небольшое сообщение по теме «Использование явления  теплопроводности в различных областях человеческой деятельности».  3.Подведение итогов урока (4мин) Давайте вспомним, какова была цель урока, чему мы должны были научиться  за урок, всех ли целей мы достигли? Что такое теплопроводность?  Как протекает теплопроводность в газах, жидкостях и твердых телах? Методические рекомендации по проведению урока Разработанный урок по теме «Теплопроводность» предназначен для  проведения в 8 классе.  Уровень изучения физики – базовый (2 часа в неделю).  В ходе урока учитель подводит обучающихся к проблемным ситуациям,  сталкиваясь с которыми дети понимают необходимость изучения темы и  отдельных моментов тем. Первая проблемная ситуация – перейдем к изучить  способ теплопередачи, а именно теплопроводность; вторая – научиться  применять свои знания при решении заданий.  В ходе урока предполагается самостоятельная работа обучающихся с  дальнейшим самооцениванием. Обучающиеся выполняют работу на нетбуках.  Кабинет физики оборудован нетбуками, их количества достаточна для того  чтобы каждый ребенок работал за своим компьютером. В таком режиме  работать привыкли, поэтому не тратиться времени на инструктаж. Нетбуки  включены заранее на перемене, обучающиеся выбирают только номер  необходимого теста и начинают работу.  При выставлении отметок учитывается работа обучающихся на протяжении  всего урока, а именно устные ответы на вопросы учителя, помощь учителю при проведении опытов, самостоятельная работа с дальнейшей  самопроверкой, решение заданий на закрепление материала.  Отметка может  выводиться как среднее арифметическое всех отметок, полученных на  каждом этапе урока. В ходе урока обучающиеся заполняют листы  самооценивания. С листом самооценивания обучающиеся работают  практически на каждом уроке.  Приложением к разработанному уроку является технологическая карта. Список литературы:   1. Волков В.А. Поурочные разработки по физике:8класс. – 3 –е изд., перераб.  и доп. – М.:ВАКО,2009.­368с. 2. Гутник Е.М. Физика. 8 кл.: тематическое и поурочное планирование к  учебнику А.В.Перышкина «Физика. 8 класс»/ Е.М.Гутник, Е.В. Рыбакова,  Е.В. Шаронина: под ред. Е.М.Гутник.­ 3­е изд., стереотип._М.: Дрофа,  2005.­95с. 3. Марон Е.А. Опорные конспекты и разноуровневые задания. К учебнику для общеобразовательных учебных заведений А.В.Перышкин «Физика. 8  класс». ­ СПб.: ООО «Виктория плюс», 2009. ­ 96 4. Перышкин  А.В. Физика. 8 кл.:учеб. для общеобразоват. учреждений /  А.В.Перышкин. – М.:Дрофа, 2013. – 237. 5. Чеботарева А.В. Тесты по физике. 8 класс: к учебнику А. В. Перышкина  «Физика. 8 кл.»/­8­е изд., перераб. и доп.­М.:Издательство  «Экзамен»,2014.­222 с.

ЛЕКЦИЯ 06 Тема: Теория теплообмена. Теплопроводность.

ЛЕКЦИЯ  06

Тема: Теория теплообмена. Теплопроводность.

План лекции: 1. Введение в теорию теплообмена.

2.Теплопроводность. Основные понятия и определения.

3. Основной закон и уравнение теплопроводности.

4. Условия однозначности.

1. Введение в теорию теплообмена

В теории теплообмена изучаются закономерности переноса теплоты из одной области пространства в другую, которые представляют собой процессы обмена внутренней энергией между элементами рассматриваемой системы в форме теплоты.

Существует три различных по своей природе элементарных вида теплообмена: теплопроводность, конвективный теплообмен и лучистый теплообмен.

Теплопроводность в чистом виде, как правило, встречается только в твердых телах. Так, в диэлектриках перенос теплоты осуществляется за счет распространения упругих волн колеблющихся атомов и молекул, в металлах он связан с перемещением свободных электронов и колебаниями атомов кристаллической решетки.

Конвективный теплообмен может иметь место в движущихся средах (жидкостях и газах). При наличии разности температур в различных точках среды перемещение макрочастиц в процессе конвекции всегда сопровождается теплопроводностью.

Теплоотдача – наиболее распространенный случай конвективного теплообмена. Чаще всего конвективный теплообмен в процессе теплоотдачи осуществляется между движущейся средой и поверхностью обтекаемого средой твердого тела, например, процесс теплоотдачи при течении жидкости в трубах, внешнем обтекании тел газом.

Лучистый теплообмен между телами может осуществляться и при отсутствии промежуточной среды (в вакууме). Он обусловлен только температурой и оптическими свойствами тел, участвующих в теплообмене.

Массообмен характерен для процессов теплообмена в многокомпонентных средах. Аналогично процессам переноса теплоты перенос вещества в смеси может быть обусловлен тепловым движением микрочастиц (диффузия) и движением макроскопических элементов среды (конвективный массообмен).

Теплообмен – самопроизвольный необратимый процесс переноса теплоты в пространстве с неоднородным распределением температуры.

Теплопроводность – молекулярный перенос теплоты в сплошной среде, обусловленный наличием градиента температуры.

Конвективный теплообмен – перенос теплоты, обусловленный перемещением макроскопических элементов среды в пространстве, сопровождаемый теплопроводностью.

Теплоотдача – конвективный теплообмен между движущейся средой и поверхностью ее раздела с другой средой (твердым телом, жидкостью или газом).

Лучистый теплообмен – теплообмен, обусловленный превращением внутренней энергии вещества в энергию электромагнитных волн, распространением их в пространстве и поглощением энергии этих волн веществом.

Массообмен – самопроизвольный необратимый процесс переноса массы данного компонента в пространстве с неоднородным полем концентрации (химического потенциала).

2. Теплопроводность

Аналитическая теория теплопроводности применима только к сплошной среде, поэтому при расчете процессов теплопроводности не учитывается дискретное строение тел, принимается, что тела гомогенны и изотропны, а размеры их велики по сравнению с расстоянием между молекулами.

Температурное поле может быть нестационарным и стационарным. В первом случае поле изменяется во времени, во втором – нет. В соответствии с этим процесс считается стационарным или нестационарным.

Поверхность, во всех точках которой температура одинакова, называется изотермой. Такие поверхности не пересекаются между собой. Они могут быть замкнутыми или кончаются на границах тела. Наиболее резкое изменение температуры в теле с неоднородным температурным полем наблюдается в направлении нормали к изотермной поверхности.

Градиент температуры направлен в сторону повышения температуры

grad T=ÑT = lim(DT/Dn) = dT/dn , где Ñ – символический вектор

Dn®0 (оператор Гамильтона), заменяющий символ градиента (а также дивергенции и ротации).

Поле температурного градиента является векторным, поэтому

(*)

где координаты градиента; i, j, k – единичные векторы, имеющие направление координатных осей.

Тепловой поток, отнесенный к единице площади поверхности, называется плотностью теплового потока q. Плотность теплового потока может быть местной (локальной) и средней по поверхности; является вектором, направленным в сторону падения температуры. Совокупность значений плотности теплового потока во всех точках тела в данный момент времени образует векторное поле плотности теплового потока. Линия, в каждой точке которой вектор плотности теплового потока направлен по касательной к ней, называется линией теплового тока.

3. Основной закон и уравнение теплопроводности

Опытным путем установлено, что плотность теплового потока, передаваемого теплопроводностью, прямо пропорциональна градиенту температуры:

(1)

где l – коэффициент теплопроводности, определяемый опытным путем и зависящий от агрегатного состояния вещества, температуры, давления, структуры, плотности, пористости и влажности. Знак минус указывает на то, что векторы q и grad T имеют противоположное направление.

Уравнение (1) является математическим выражением закона теплопроводности ФУРЬЕ, а значение l характеризует интенсивность процесса теплопроводности и числено равно плотности теплового потока при градиенте температуры, равном единице. Количество теплоты Q_t, теряемое произвольным объемом V внутри тела, можно определить путем интегрирования плотности теплового потока q по замкнутой поверхности S, ограничивающей этот объем так, что

где – единичный вектор, направленный по нормали к поверхности; t – время.

Используя формулу Остроградского-Гаусса, получим:

. (2)

В соответствии с первым законом термодинамики это количество теплоты может появиться лишь за счет уменьшения внутренней энергии единицы объема тела в единицу времени

, а также за счет действия внутренних источников теплоты мощностью q_V (Вт/м³), которые могут иметь различную физическую природу. Поэтому

(3)

где с – удельная теплоемкость тела.

Левые части выражений (2) и (3) равны, поэтому

Так как объем V выбран произвольно, равенство нулю интеграла означает, что

(4)

Перенос теплоты в твердом теле осуществляется путем теплопроводности, поэтому с учетом уравнения (1) и соотношения уравнение теплопроводности примет вид:

(5)

Уравнение (5) можно записать в виде

(6)

где а – коэффициент температуропроводности, характеризующий скорость выравнивания температуры неравномерно нагретого тела (м²/с). При отсутствии внутренних источников теплоты и с учетом уравнения (*) можно получить

(6a)

Уравнения (6, 6а) выражают зависимость изменения во времени температуры в некоторой точке тела от свойств тела и производительности источников теплоты в окрестности этой точки, т.е. устанавливают связь между пространственными и временными изменениями температуры. Для получения однозначного решения уравнений (6, 6а) необходимо выполнение следующих условий, которые называют условиями однозначности.

4. Условия однозначности

– геометрические, согласно которым задаются форма и размеры твердого тела;

– физические, определяющие физические свойства тела l, с и r или их зависимостями от температуры;

– начальные, устанавливающие распределение температуры в теле в начальный момент времени;

– граничные первого, второго и третьего рода. Граничные условия первого рода определяют температуру на поверхности тела как функцию координат и времени. Согласно граничным условиям второго рода задается плотность теплового потока (или составляющая градиента температуры, нормальная поверхности тела) на поверхности тела в виде функции координат поверхности тела и времени. Граничные условия третьего рода – задание температуры жидкой или газовой среды, окружающей твердое тело, и закона теплообмена между телом и средой.

Аналитическое выражение граничных условий третьего рода может быть получено с помощью закона теплоотдачи НЬЮТОНА

q = a(T_w – T_f). (7)

Коэффициент теплоотдачи a определяет интенсивность теплоотдачи с поверхности. Количество теплоты, соответствующее значению q должно подводиться к поверхности тела путем теплопроводности изнутри, поэтому

q = -l(grad_nT)_w, (8)

где grad_nT – составляющая градиента температуры, нормальная к поверхности тела.

Приравнивая правые части уравнений (7) и (8), получим

a(T_w-T_f) =-l(grad_nT)_w. (9)

В соответствии с граничными условиями третьего рода значения T_f и a должны быть заданы.

Пёрышкин. Решебник по белому учебнику

§ 1. Тепловое движение. Температура

Вопросы

§ 2. Внутренняя энергия

Вопросы

Упражнение 1

Задание

§ 3. Способы изменения внутренней энергии тела

Вопросы

Упражнение 2

Задание

§ 4. Теплопроводность

Вопросы

Упражнение 3

Задание

§ 5. Конвекция

Вопросы

Упражнение 4

Задание

§ 6. Излучение

Вопросы

Упражнение 5

Задание

§ 7. Количество теплоты. Единицы количества теплоты

Вопросы

Упражнение 6

§ 8. Удельная теплоёмкость

Вопросы

Упражнение 7

Задание

§ 9. Расчёт количества теплоты, необходимого для нагревания тела или выделяемого им при охлаждении

Вопросы

Упражнение 8

§ 10. Энергия топлива. Удельная теплота сгорания

Вопросы

Упражнение 9

Задание

§ 11. Закон сохранения и превращения энергии в механических и тепловых процессах

Вопросы

Упражнение 10

§ 12. Агрегатные состояния вещества

Вопросы

§ 13. Плавление и отвердевание кристаллических тел

Вопросы

Упражнение 11

Задание

§ 14. График плавления и отвердевания кристаллических тел

Вопросы

Задание

§ 15. Удельная теплота плавления

Вопросы

Упражнение 12

Задание

§ 16. Испарение. Насыщенный и ненасыщенный пар

Вопросы

Задание

§ 17. Поглощение энергии при испарении жидкости и выделение её при конденсации пара

Вопросы

Упражнение 13

Задание

§ 18. Кипение

Вопросы

Упражнение 14

Задание

§ 19. Влажность воздуха. Способы определения влажности воздуха

Вопросы

Упражнение 15

§ 20. Удельная теплота парообразования и конденсации

Вопросы

Упражнение 16

Задание

§ 21. Работа газа и пара при расширении

Вопросы

§ 22. Двигатель внутреннего сгорания

Вопросы

§ 23. Паровая турбина

Вопросы

§ 24. КПД теплового двигателя

Вопросы

Упражнение 17

Задание

Проверь себя

§ 25. Электризация тел при соприкосновении. Взаимодействие заряженных тел

Вопросы

Упражнение 18

Задание

§ 26. Электроскоп

Вопросы

§ 27. Электрическое поле

Вопросы

Упражнение 19

§ 28. Делимость электрического заряда. Электрон

Вопросы

§ 29. Строение атомов

Вопросы

Упражнение 20

§ 30. Объяснение электрических явлений

Вопросы

Упражнение 21

§ 31. Проводники, полупроводники и непроводники электричества

Вопросы

Упражнение 22

§ 32. Электрический ток. Источники электрического тока

Вопросы

Задание

§ 33. Электрическая цепь и её составные части

Вопросы

Упражнение 23

§ 34. Электрический ток в металлах

Вопросы

Задание

§ 35. Действия электрического тока

Вопросы

Задание

§ 36. Направление электрического тока

Вопросы

§ 37. Сила тока. Единицы силы тока

Вопросы

Упражнение 24

§ 38. Амперметр. Измерение силы тока

Вопросы

Упражнение 25

§ 39. Электрическое напряжение

Вопросы

§ 40. Единицы напряжения

Вопросы

§ 41. Вольтметр. Измерение напряжения

Вопросы

Упражнение 26

§ 42. Зависимость силы тока от напряжения

Вопросы

Упражнение 27

§ 43. Электрическое сопротивление проводников. Единицы сопротивления

Вопросы

Упражнение 28

§ 44. Закон Ома для участка цепи

Вопросы

Упражнение 29

§ 45. Расчёт сопротивления проводника. Удельное сопротивление

Вопросы

§ 46. Примеры на расчёт сопротивления проводника, силы тока и напряжения

Упражнение 30

§ 47. Реостат

Вопросы

Упражнение 31

§ 48. Последовательное соединение проводников

Вопросы

Упражнение 32

§ 49. Параллельное соединение проводников

Вопросы

Упражнение 33

§ 50. Работа электрического тока

Вопросы

Упражнение 34

§ 51. Мощность электрического тока

Вопросы

Упражнение 35

§ 52. Единицы работы электрического тока, применяемые на практике

Вопросы

Упражнение 36

Задание

§ 53. Нагревание проводников электрическим током. Закон Джоуля—Ленца

Вопросы

Упражнение 31

§ 54. Конденсатор

Вопросы

Упражнение 38

Задание

§ 55. Лампа накаливания. Электрические нагревательные приборы

Вопросы

Задание

§ 56. Короткое замыкание. Предохранители

Вопросы

Проверь себя

§ 57. Магнитное поле

Вопросы

Упражнение 39

§ 58. Магнитное поле прямого тока. Магнитные линии

Вопросы

Упражнение 40

§ 59. Магнитное поле катушки с током. Электромагниты и их применение

Вопросы

Упражнение 41

Задание

§ 60. Постоянные магниты. Магнитное поле постоянных магнитов

Вопросы

Упражнение 42

Задание

§ 61. Магнитное поле Земли

Вопросы

Упражнение 43

Задание

§ 62. Действие магнитного поля на проводник с током. Электрический двигатель

Вопросы

Задание

Проверь себя

§ 63. Источники света. Распространение света

Вопросы

Упражнение 44

Задание

§ 64. Видимое движение светил

Вопросы

Задание

§ 65. Отражение света. Закон отражения света

Вопросы

Упражнение 45

§ 66. Плоское зеркало

Вопросы

Упражнение 46

§ 67. Преломление света. Закон преломления света

Вопросы

Упражнение 47

§ 68. Линзы. Оптическая сила линзы

Вопросы

Упражнение 48

§ 69. Изображения, даваемые линзой

Вопросы

Упражнение 49

§ 70. Глаз и зрение

Вопросы

Задание

Проверь себя

Лабораторные работы

Теплопроводность | Образовательные инновации

Автор: Мартин Загендорф

Простой вопрос: Какой теплее – какой кулер ?

В самом строгом смысле это вопрос энергии. И мы используем температуру как меру уровня энергии. Как мы все знаем, чем больше уровень энергии, тем выше температура… Но, хотя это абсолютно верно; иногда это , а не то, что мы воспринимаем в повседневной жизни.Когда нас спрашивают, все мы можем засвидетельствовать, что, когда мы дотрагиваемся до куска металла, мы говорим, что он холодный. Но действительно ли холодно? Это или , не правда ли «холодно»?

Ответ…

… очень просто. Если кусок металла имеет комнатную (окружающую) температуру, он не может быть «холодным» – он должен быть при той же температуре , что и температура в помещении.

Но сначала:

Давайте обсудим «воспринимаемую температуру» : это то, что мы «думаем» , это температура.Это не всегда фактическая температура (объекта, которого мы касаемся). Таким образом, мы вступаем в чудесное сочетание физики и биологии. Физика описывает абсолюты. Биология описывает биологические реакции (интерпретации) нашего физического мира.

Дело в теплопроводности и наших нервов. Некоторые материалы являются хорошими проводниками тепла (энергии), а некоторые – нет. Наши нервы воспринимают только температуру – поэтому, если тепловая энергия быстро отводится от тканей, окружающих наши нервные окончания (например, кончиков пальцев), наши нервы ощущают, что температура, «которую они ощущают», ниже, e.грамм. материал удаляет тепловую энергию из тканей тела, окружающих нервные окончания, быстрее, чем наше тело может повторно поставлять энергию тканям – поэтому наши нервы воспринимают это как «холоднее».

Сейчас:

По-настоящему наглядный и запоминающийся способ постановки вопроса:

Используйте конструкцию, которая позволяет «ощущать» температуру трех различных материалов: всех трех с разной теплопроводностью – низкой, средней и высокой – простой ящик с квадратами из керамики, дерева и алюминия.Керамические и алюминиевые детали имеют почти одинаковую теплопроводность, но алюминий имеет чуть лучшую теплопроводность. Древесина имеет относительно низкую теплопроводность.

Эта коробка имеет ширину 17 дюймов, высоту 8 дюймов и глубину 3 дюйма.

In The Classroom, Обсудить:

Тепловая энергия в материалах

Температура (как мера тепловой энергии)

Электропроводность (тепловой энергии)

[обратите внимание, что вы еще не представили биологический аспект предстоящего измерения учащимися того, что теплее или холоднее]

Упражнение по теплопроводности:

Начните с рисования трех столбцов «Список голосов» на классной доске (АЛЮМИНИЙ – ДЕРЕВО – КЕРАМИКА).

[это немного умышленное отвлечение, но перед запуском переведите переключатель в положение ВКЛ и сосчитайте до пяти секунд]

Попросите учащихся по очереди «протестировать» (прикоснувшись) к трем материалам и отметить свой голос на доске.

Всего голосов.

Спросите класс, имеет ли это смысл … что алюминиевая (или, возможно, керамическая) деталь самая крутая? Спросите: «Почему это так?»… «Это потому, что металл или керамика тяжелее?»… Или: «Это потому, что дерево темнее по цвету?»

Теперь поверните коробку, чтобы показать ее внутренности – внутри коробки ничего .Три куска материала ДОЛЖНЫ быть при одинаковой температуре! – Комнатная температура. Если кто-то из студентов все еще сомневается в вас, используйте ИК-термометр, чтобы доказать свою точку зрения!

И наконец:

Самая интересная часть урока: спросите класс: «Почему так много людей думали, что один материал« круче », чем два других?» Не давайте ответа – ведите обсуждение – позвольте классу найти ответ.

Марти Загендорф – физик и учитель на пенсии; он твердо верит в ценность практического опыта при изучении физики.Он является автором книги «Демонстрационный аппарат физики». Эту удивительную книгу можно приобрести в компании «Образовательные инновации» – она ​​включает в себя идеи и конструктивные детали для создания и использования широкого спектра впечатляющих демонстраций физики и лабораторного оборудования. Включено 49 подробных разделов, описывающих практическое устройство, иллюстрирующее механические, электрические, акустические, тепловые, оптические, гравитационные и магнитные темы. Эта книга также включает разделы, посвященные советам и подсказкам, источникам материалов и воспроизводимым этикеткам.

Эта запись была опубликована в субботу, 26 ноября 2011 г., в 16:02 и находится в разделах «Биология», «Элементарный уровень», «Уровень средней школы», «Уровень средней школы», «Физика». Вы можете следить за любыми ответами на эту запись через канал RSS 2.0. Вы можете оставить отзыв или откликнуться со своего сайта.

Сообщение навигации

” Предыдущий пост Следующее сообщение »

Интегрированный подход к проектированию и разработке высокопроизводительного полимерно-композиционного материала для термоинтерфейса

Abstract

Вычислительная структура, основанная на новой аппроксимации дифференциальной эффективной среды и гомогенизации среднего поля, используется для разработки высокоэффективной термической границы раздела полимеров с наполнителем материалы (ТИМ).Предлагаемая стратегия проектирования позволяет справиться с концентрацией неразбавленного наполнителя в полимерной матрице. Эффективная теплопроводность предполагаемых композитов с термоинтерфейсом может быть адаптирована в широком диапазоне путем изменения атрибутов наполнителя, таких как размер, соотношение сторон, ориентация, а также граница раздела наполнитель-матрица с верхним пределом, налагаемым модулем сдвига. На этапе проектирования учитываются потенциальные полимеры и наполнители сервала. Полиэтилен высокой плотности (HDPE) и термопластичный полиуретан (TPU) с неразбавленной концентрацией (~ 60 об.%) Керамических наполнителей демонстрируют высокую теплопроводность (4–5 Вт · м ⁻¹ K ⁻¹ ) без компромиссов. высокое соответствие ТИМов.Прогнозируемая теплопроводность и коэффициент теплового расширения прекрасно согласуются с данными измерений различных бинарных композитных систем, включая полиэтилен высокой плотности, ТПУ и полипропилен (ПП), наполненные Al ₂ O ₃ и наполнителями AlN различных размеров, форм, и концентрации, полученные посредством смешивания в расплаве и компрессионного формования. Модель также подтверждает, что манипулирование выравниванием наполнителя и соотношением сторон может значительно способствовать созданию теплопроводных сетей в композитах, что приводит к сверхвысокой теплопроводности.

Ключевые слова: интерфейс , конструкция, композиты, полимер, термическое сопротивление

1. Введение

Термоинтерфейсный материал (TIM) является важной частью для эффективного отвода тепла, генерируемого в полупроводниковых микросхемах электронных устройств, которые подвергаются воздействию к термоциклическому процессу. Передача тепла через границы раздела между материалами становится узким местом для теплопроводности, учитывая растущую тенденцию к миниатюризации микроэлектроники [1].В типичном корпусе электроники, как показано на рисунке, модули TIM обычно применяются на стыках между двумя твердыми модулями, как правило, между тепловыделяющим кристаллом и теплораспределителем, а также между теплораспределителем и радиатором. Тепловые характеристики TIM в основном оцениваются по сопротивлению теплового интерфейса ( R _TIM ), которое является мерой общего сопротивления рассеиванию тепла через интерфейс. Это связано с перепадом температуры на границе раздела по закону Фурье.После применения TIM между твердотельными модулями эффективное тепловое сопротивление ( R _TIM ) на границе раздела будет иметь две составляющие, то есть объемное сопротивление TIM, обусловленное его конечной теплопроводностью, λ _eff и контактное сопротивление R _c между TIM и соседними модулями. R _TIM может быть выражено как [2]

где BLT – толщина линии соединения TIM, а R _TIM , R _{c 1} и R _{c 2} измеряются как термические сопротивления, нормированные по площади (K · m ² Вт ^-1 ).Идеальный TIM должен состоять из материала, сочетающего низкий BLT с высокой теплопроводностью и низким тепловым контактным сопротивлением на границах раздела. Целью данной статьи является снижение R _TIM за счет разработки полимерного композита с улучшенными характеристиками λ _eff вместе с улучшенными структурными характеристиками и диэлектрическими характеристиками путем выбора подходящих наполнителей и полимерных матриц. Кроме того, сопротивление теплового контакта между TIM и присоединенными модулями ( R _{c 1} и R _{c 2} ) также является важным фактором, на который существенно влияет тип полимерной матрицы и наполнитель.

Типичная структура материалов термоинтерфейса (ТИМ), используемых в корпусах микроэлектроники.

Тепловые свойства как основная проблема вместе с механикой контакта и электрическими свойствами являются основными соображениями при проектировании TIM в зависимости от области применения. Другим требованием к TIM является соответствующее механическое поведение с точки зрения хорошей механической податливости и смачиваемости или способность заполнять пустоты, ведущие к увеличению площади контакта.Низкая прочность на сдвиг для улучшенной формуемости является фундаментальным требованием, которое обеспечивает необходимое изменение формы и межфазный контакт с сопрягаемыми модулями. Для большинства электронных приложений требуется, чтобы ТИМ имели низкую диэлектрическую проницаемость, высокое электрическое сопротивление и высокую прочность на пробой [3]. Загрузка неорганических наполнителей в полимерные композитные ТИМы приводит к значительному полю пробоя, которое зависит от содержания, формы, размера, смачиваемости матрицей, дисперсии и электрических свойств этих наполнителей.Несоответствие диэлектрической проницаемости (для переменного тока) или электропроводности (для постоянного тока) между наполнителями и полимерными композитами приводит к искажению такого электрического поля. Следовательно, наполнители, имеющие аналогичные электрические характеристики, что и ТИМ с полимерной матрицей, необходимы для снижения интенсивности искажения поля.

Обычный ТИМ состоит из теплопроводных полимерных композитов, которые состоят из полимерных матриц, заполненных теплопроводными частицами (керамика, углеродные материалы или металлы) для достижения необходимой теплопроводности при сохранении типичных вязких свойств полимера. матрица.Кроме того, полимерно-композитный наполнитель обычно используется в качестве ТИМ благодаря его электроизоляции и простоте обработки. Однако его использование в промышленности по-прежнему ограничено из-за низкой теплопроводности полимера в качестве матрицы из-за его высокой формуемости и эффективности упаковки. Чтобы преодолеть проблему низкой теплопроводности, в полимерных матрицах используются наполнители с высокой теплопроводностью, такие как керамика, металлы и материалы на основе углерода, такие как УНТ, алмаз и графит. Более того, многочисленные методы, такие как функционализация поверхности, выравнивание наполнителя и оптимизация структуры, также исследуются для повышения теплопроводности через полимерные композитные ТИМ.

Среди доступных потенциальных наполнителей, используемых в TIM на полимерной основе, керамика, такая как оксид алюминия (Al ₂ O ₃ ), нитрид кремния (Si ₃ N ₄ ), карбид кремния (SiC), нитрид бора. (BN) и нитрид алюминия (AlN) широко используются благодаря их стабильности, желаемой электрической изоляции и достаточно высокой теплопроводности. Глинозем (Al ₂ O ₃ ) является наиболее часто используемым кандидатом в наполнитель из-за его низкой стоимости и относительно высокой теплоизоляции, несмотря на его сравнительно низкую теплопроводность (~ 30 Вт · м ^-1 K ^-1 ) [4 ].Многие другие кандидаты в наполнители, такие как углеродные нанотрубки / нановолокна [5] и графит / графен [6], также используются в качестве наполнителей в ТИМ из-за их чрезвычайно высокой теплопроводности. Несмотря на то, что монослой графена, как сообщается, имеет очень высокую теплопроводность (~ 1000 Вт · м ^-1 K ^-1 ) при комнатной температуре, его теплопроводность сильно ухудшается из-за собственного рассеяния окружающей среды при сборке в жгуты. Значительно изменяющаяся собственная теплопроводность графита из-за его анизотропной природы создает еще одну проблему для его использования в качестве ТИМ.Тепловая граница раздела между матрицей и наполнителями дополнительно приводит к рассеянию и, таким образом, ставит под угрозу преимущества этих наполнителей с высокой теплопроводностью. Например, сообщается, что композиты графен-полимер и УНТ-полимер часто имеют теплопроводность ниже 1 Вт · м ^-1 K ^-1 , несмотря на неразбавленные концентрации, которые связаны со слабой ван-дер-ваальсовой связью в наполнителе. интерфейсы, где транспорт фононов в значительной степени затруднен [3,7]. Хуанг и др. [8] сообщили, что управление ориентацией нанопроволок SiC в эпоксидных композитах может обеспечивать сверхвысокую теплопроводность в плоскости (~ 10 Вт · м ⁻¹ K ⁻¹ ) при очень низкой концентрации наполнителя (5 мас.%) По сравнению с случайная загрузка нанопроволок SiC в эпоксидную смолу, в результате чего только 1.78 Вт · м ⁻¹ K ⁻¹ .

Полимерные композитные ТИМы являются наиболее широко используемыми кандидатами, поскольку они, как правило, мягкие и гибкие, чтобы преодолевать механические проблемы, такие как расслоение, растрескивание и образование пустот, когда электронные блоки подвергаются изменению температуры, ведущему к термическим напряжениям, из-за несоответствия в коэффициенте тепловое расширение (КТР) различных интерфейсов [9]. Следовательно, желательно поддерживать низкий модуль упругости полимерных композитов при нагружении твердых наполнителей, чтобы обеспечить лучшее заполнение пустот между ТИМ и подложками.Более того, пониженный КТР также необходим для уменьшения несоответствия с соседними границами раздела керамических полупроводников, что приводит к снижению уровней индуцированных термических напряжений. Основным ограничением тепловых характеристик в результате использования полимеров в TIM является чрезвычайно низкая теплопроводность (~ 0,1–0,3 Вт м ^-1 K ^-1 ). Чтобы компенсировать это ограничение, значительные усилия прилагаются к использованию полимерных ТИМов с добавлением подходящих наполнителей. Некоторые распространенные наполнители, о которых сообщается в литературе, включают силикон [2], полиэтилен [10], полипропилен [11], полиамид [12], поливинилхлорид и эпоксидные смолы [13].Ральфс и др. [14] сообщили, что магнитно-индуцированная перколяция частиц никеля в силиконовой матрице удваивает теплопроводность композита из-за увеличения контакта между частицами.

Эффективные свойства композитов являются взаимосвязанными функциями их составляющих на атомном и микроструктурном уровнях. Например, эффективная теплопроводность ТИМ типа наполнителя является функцией собственной теплопроводности матрицы и наполнителя, объема наполнителя и сопротивления термоинтерфейса (также называемого сопротивлением капице) между наполнителями и матрицей.Это сопротивление дополнительно зависит от размера, формы и поверхностной проводимости материала наполнителя. Огромные экспериментальные усилия и затраты связаны с выбором правильных комбинаций различных атрибутов этих составляющих для достижения целевых свойств. В настоящее время большое количество исследований сосредоточено на разработке вычислительных инструментов, которые могут предсказывать индивидуальные эффективные функциональные свойства предполагаемых композитов.

Теория эффективной среды была инициирована Максвеллом для оценки свойств композитов с невзаимодействующими сферическими (3D) наполнителями.Поступали сообщения о различных модификациях модели Максвелла. Например, модель Брюггемана [15] была модифицирована, чтобы позволить модели для неразбавленных концентраций наполнителей, Гамильтона и Кроссера [16] модифицировали модель Максвелла, чтобы включить обобщенный фактор формы, а Хассельман и Джонсон (HJ) [17] включают эффект межфазного термического сопротивления (ITR). Позже Every et al. [18] модифицировали модель Брюггемана, включив в нее термическое сопротивление интерфейса HJ, которое затем модифицировали Jiajun et al.[19], чтобы включить фактор, зависящий от сферичности, с возможностью обработки наполнителей различной формы. Nan et al. [20] опубликовали теорию эффективной среды, учитывающую соотношение сторон и ориентацию наполнителей с допущением о правильной форме эллипсоидных наполнителей и разбавленных концентрациях. Впоследствии их модель была модифицирована Сиддики и соавт. [21] и Raza et al. [22] для неравномерно распределенных разбавленных гибридных наполнителей и перколяционных разбавленных гибридных наполнителей соответственно. Исходная модель Нана и ее расширения применимы к широкому диапазону форм частиц наполнителя, но эти модели ограничены разбавленными концентрациями наполнителей.В данной работе модель расширена для рассмотрения неразбавленных концентраций наполнителя (высокая объемная нагрузка) с использованием дифференциальной схемы для прогнозирования эффективной теплопроводности ТИМов с наполнителем.

Настоящая статья сосредоточена на стратегии разработки новых полимерных ТИМов с наполнителем, с повышенной теплопроводностью и заданным коэффициентом теплового расширения (КТР) и модулем сдвига (G) в качестве функциональных свойств. Объясняется реализация схемы вычислительного проектирования на основе модифицированной дифференциальной эффективной среды и усреднения среднего поля.Считается, что несколько комбинаций полимерных матриц и наполнителей с разжиженными или неразбавленными концентрациями, размером частиц и другими характеристиками материалов обеспечивают целевые свойства ТИМов. Некоторые репрезентативные составные образцы синтезируются в соответствии с прогнозами, а полученные свойства измеряются для проверки.

2. Вычислительные модели

2.1. Приближение дифференциальной эффективной среды для определения эффективной теплопроводности

Различные расширения модели Нана [20] были ранее сообщены автором и его сотрудниками [22,23].Исходная модель и ее расширения применимы к широкому диапазону форм частиц наполнителя, но эти модели ограничены разбавленными концентрациями наполнителей. Существующая модель модифицирована на основе дифференциальной теории эффективной среды Бруггемана, в которой неразбавленное согласование наполнителя (более высокая загрузка наполнителя) достигается за счет рассмотрения дифференциальной формы отношения доли низкого объема и интеграции эффектов малых приращений. В дифференциальной схеме более высокие объемные доли или неразбавленные концентрации достигаются путем интеграции эффектов небольших приращений.Следовательно, для малых объемных фракций уравнение эффективной теплопроводности для разбавленной концентрации может быть упрощено для малых φ как

λeff, 11 = λeff, 22 = λm (1 + ∑i = 2Nφi2 [β11i (1+ 〈cos2θ〉 i) + β33i (1− 〈cos2θ〉 i)])

(2)

Для уравнения ( 2), используя аналогию модели Эври [18], дифференциальная форма и ее интегральная форма для одного наполнителя могут быть записаны следующим образом в уравнениях (3) и (4), соответственно.

dλ = (dφ1 − φ) (λ2) (β11 (1+ 〈cos2θ〉) + β33 (1− 〈cos2θ〉))

(3)

∫λmλeff2λ (β11 (1+ 〈cos2θ〉) + β33 (1− 〈cos2θ〉)) dλ = ∫0φ (11 − φ) dφ

(4)

Уравнение (4) может быть решено следующим образом:

(λeff, 11λm) 2 = 1 (1 − φ) (β11 (1+ 〈cos2θ〉) + β33 (1− 〈cos2θ〉))

(5)

Уравнение (5) может быть решено итеративно для λ _{эфф, 11} .Таким же образом можно вывести уравнение (3), чтобы получить уравнение (6), которое также может быть решено итеративно для k _{eff, 33} .

(λeff, 33λm) 2 = 1 (1 − φ) (β11 (1− 〈cos2θ〉) + β33 〈cos2θ〉)

(6)

λ _{eff, kk} в уравнениях (1) – (6) представляет эффективную теплопроводность композита по глобальной оси i ^th ( x , y или z ). λ _м – теплопроводность матрицы, а φ и ⟨cos2θ⟩ – объемная доля и фактор ориентации наполнителей, соответственно.Фактор ориентации ⟨cos2θ⟩ определяется уравнением (7):

〈cos2θ〉 = ∫ψ (θ) cos2θsinθdθ∫ψ (θ) sinθdθ

(7)

где θ – угол между глобальной осью z и локальной осью z заполнителя. ψ (θ) – функция распределения, которая описывает ориентацию частиц наполнителя эллипсоидной формы. βkki – это безразмерный коэффициент усиления вдоль локальной оси i ^th частицы. Это функция некоторых материалов и параметров обработки, описываемых уравнением (8):

βkki = λe, kki − λmλm + Lkki (λe, kki − λm)

(8)

где λe, kki – эквивалентная теплопроводность составной элементарной ячейки вдоль локальной оси частицы i ^th ( x , y или z ), как определено в уравнении (9).λe, kki – это мера эффективности наполнителя для изменения конечной TC композита.

λe, 11i = {λpi / (1 + γ11iL33iλpi / λm), для пластинчатых включений λpi / (1 + γ11iL11iλpi / λm), для других форм λe, 33i = {λpi / (1 + γ33iL11iλpi / λm), для цилиндрических включений λpi / (1 + γ33iL33iλpi / λm), для других форм

(9)

где λ _p – теплопроводность твердых частиц наполнителя, а L _kk – коэффициент деполяризации вдоль локальной оси наполнителя i ^th , как определено уравнением (10) [24].γkki – безразмерный параметр, который включает комбинированный эффект радиуса Каптизы и геометрии частицы, как определено уравнением (11).

L11i = L22i = {ξi22 (ξi2−1) −ξi2 (ξi2−1) 3 / 2cosh − 1ξi, для ξi≥1ξi22 (ξi2−1) + ξi2 (1 − ξi2) 3 / 2cos − 1ξi, для ξi <1

(10)

γkki = {(2 + 1 / ξi) αk, для ξi≥1 (1 + 2ξi) αk, для ξi <1

(11)

При ξi – это соотношение сторон Эллипсоидные частицы наполнителя, принятые как r ₃ / r ₁ , где r ₃ и r ₁ – радиусы вдоль направлений наполнителя z и x соответственно.Кроме того, α _k = (λ _m R _int ) / a _k – радиус Капицы с R _int принимается в качестве сопротивления термоинтерфейса, а – _k – радиус _{i th} эллипсоидный заполнитель вдоль оси k _th . Обратите внимание, что r ₃ представляет толщину для сплюснутых частиц (таких как пластинки или диски) или длину для вытянутых частиц (например, волокон).

2.2. Схема гомогенизации среднего поля для модуля упругости и коэффициента теплового расширения

Akhtar et al. [23] обнаружили хорошее согласие между экспериментально измеренным CTE и предсказанным гомогенизацией среднего поля Мори-Танака. Согласно схеме, эффективный тензор упругости и КТР оцениваются по формулам (12) – (14):

Ceff = piCi: Ai + (1 − pi) Cm: Am

(12)

αeff = αiI2 + pi (Ci − 1 − Cm − 1) W ((1 − pi) I4 + piW) −1

(13)

Am = [(1 − pi) I4 + piBa] −1Ai = Ba: AmBa = [ I4 + S: Cm − 1 (Ci − Cm)] – 1W = CiAiCm − 1

(14)

C _eff и α _eff – тензор гомогенизированной жесткости и эффективный CTE результирующий композит соответственно. C _i и C _m – тензоры жесткости включения и матрицы соответственно. A _m и A _i – тензоры локализации деформации; I ₂ и I ₄ – это идентификаторы 2-го и 4-го порядка соответственно; S – тензор Эшелби.

2.3. Выбор потенциальных наполнителей и полимеров

Полимеры используются в качестве матрицы в композитах в качестве ТИМ из-за их электрической изоляции, формуемости и эффективности заполнения при использовании в качестве интерфейса между модулями.Для увеличения теплопроводности матричного материала необходимы теплопроводящие наполнители. Более того, необходимо выбирать наполнители, имеющие аналогичные электрические характеристики полимерам, чтобы поддерживать высокую прочность на пробой, которая является внутренним свойством полимеров и одной из основных причин их использования в качестве ТИМов. Многочисленные полимеры рассматриваются в текущей работе как потенциальные кандидаты на основании их использования в индустрии TIM. К ним относятся полипропилен (PP), полиэтилен высокой плотности (HDPE), термопластичный полиуретан (TPU), полисульфон (PSU), эпоксидная смола и силикон.Свойства этих полимеров показаны в [25,26,27,28]. Чтобы выполнить требования TIM, несколько традиционных и новых керамических наполнителей и наполнителей на основе углерода рассматриваются в качестве потенциальных кандидатов с учетом их теплопроводности, электрической изоляции, стабильности и диэлектрических свойств. Из-за высокой электропроводности металлические наполнители не рассматриваются в существующей конструкции. Кандидаты в потенциальные наполнители и их свойства перечислены в. Нитрид алюминия (AlN), нитрид кремния (Si ₃ N ₄ ), нитрид бора (BN) и карбид кремния (SiC) включены в качестве наполнителей из-за их электрической изоляции, стабильности и достаточно высокой теплопроводности.Несмотря на относительно низкую теплопроводность, оксид алюминия (Al ₂ O ₃ ) считается из-за его низкой стоимости и высокого удельного электрического сопротивления. Полупроводниковый нитрид галлия (GaN) считается новым материалом с высокой теплопроводностью, что позволяет увидеть его применимость в качестве наполнителя.

Таблица 1

Свойства потенциальных матриц и наполнителей для термоинтерфейсного материала [25,26,27,28].

Рассматриваемые потенциальные полимеры и наполнители	Теплопроводность ( Вт м −1 K −1 )	Коэффициент Пуассона	Модуль упругости (ГПа) Сдвиг (ГПа)	Коэффициент теплового расширения (10 −6 K −1 )
Полимерные матрицы
Термопластический полиуретан (ТПУ)	0.22	0,49	0,0035	0,00112	190
Полиэтилен высокой плотности (HDPE)	0,45	0,46	0,8	0,274	150
Полипропилен (ПП)	0,15	0,43	1,4	0,49	100
полисульфон	0,26	0,37	2,48	0.905	56
Эпоксидная	0,185	0,32	3,45	1,31	55
Силикон	0,2	0,47	0,028	0,0094	270
Наполнители
Глинозем (Al 2 O 3 )	33	0,21	370	88.0	4,6
Нитрид алюминия (AlN)	177	0,23	330	126	4,3
Нитрид галлия (GaN)	130	0,25	306	122,4	3,1
Карбид кремния (SiC)	170	0,21	430	177,7	4,0
Нитрид бора (BN)	52	0.21	41	41,0	6,0
Нитрид кремния (Si 3 N 4 )	43	0,23	310	65,3	1,4
Бриллиант	2000	0,2	850	440	0,8
Графит	180	0,2	21	8,75	4.9

3. Материалы и методы эксперимента

3.1. Материалы

Синтезировано несколько полимерных композитных систем с различными матрицами и атрибутами наполнителя для проверки предложенного расчетного дизайна. Разработка композита включала предварительную обработку частиц наполнителя, смешивание ингредиентов в расплаве, прессование, измерения и микроскопию. Al ₂ O ₃ и AlN выбраны в качестве наполнителей, в то время как HDPE, PP и TPU оказались наилучшей потенциальной матрицей на основе композитной конструкции.Порошки AlN и гранулы HDPE поставляются Surmet Corporation (Берлингтон, Массачусетс, США) и SABIC (Эр-Рияд, KSA) соответственно, а порошки Al ₂ O ₃ , γ-метилакрилоксипропилтриметоксисилан (для обработки поверхности) и PP гранулы приобретаются у Sigma Aldrich (Сент-Луис, Миссури, США). ПУ поставляла компания Taiwan PU Corporation (г. Нью-Тайбэй, Тайвань). Поверхность частиц наполнителя была обработана в соответствии с методом, описанным ранее [29], для улучшения совместимости поверхности раздела с полимерной матрицей.К этанолу добавляли 2 мас.% Γ-метилакрилоксипропилтриметоксисилана и перемешивание проводили в течение 3 минут при комнатной температуре. Затем постепенно по каплям добавляли HCl для доведения pH до значения 5 с последующим перемешиванием в течение 10 минут. Затем к приготовленному раствору добавляли предварительно взвешенные керамические порошки (Al ₂ O ₃ или AlN) и перемешивали в течение 20 минут при комнатной температуре с последующим дополнительным перемешиванием в течение 40 минут при 70 ° C. Затем обработанным частицам давали отстояться в течение 1 ч перед выливанием.Затем проводили ночную сушку частиц при 90 ° C с использованием вакуумной печи. Обработанные порошки затем хранили в вакуумном эксикаторе, чтобы избежать загрязнения пылью или влагой.

3.2. Разработка композитов

Предварительно взвешенные количества полимерных гранул и предварительно обработанных керамических порошков (Al ₂ O ₃ или AlN) смешивали в расплаве в соответствии с проектными объемными долями при 150 ° C со скоростью 60 об / мин в течение 20 минут с использованием измерительного смесителя Brabender. 50 EHT. После достижения заданных температур (диапазон: 150–180 ° C) в смесительной камере гранулы полимера и предварительно взвешенные керамические порошки добавляли при более медленных оборотах (30 об / мин) с последующим смешиванием двух фаз при 60 об / мин в течение 30 мин.Затем эти композитные комки были обработаны, чтобы сделать образцы желаемой формы для измерений. Затем предварительно взвешенные куски подвергаются горячему прессованию в машине для формования под давлением при температуре плавления матрицы для конкретного состава в виде дискообразных образцов (диаметром 31 мм) необходимой толщины.

3.3. Испытания

Теплопроводность образцов измеряется с помощью анализатора теплопроводности TCi производства C-Therm Technologies Ltd., Фредериктон, Северная Каролина, Канада.Это оборудование измеряет теплопроводность на основе метода модифицированного источника переходной плоскости, в котором используется односторонний датчик межфазного теплоотражения с переходным постоянным источником тепла к образцу. Коэффициент теплового расширения композитов измеряется с помощью термомеханического анализатора МЕТТЛЕР ТОЛЕДО (TMA / SDTA 1 LF / 1100, МЕТТЛЕР ТОЛЕДО, Колумбус, Огайо, США). Это оборудование измеряет изменение размеров композита в зависимости от температуры. Возникающее в результате смещение в результате изменения размеров обнаруживается датчиком, помещенным на образец, с помощью датчика линейного переменного дифференциального трансформатора (LVDT), подключенного к другому концу датчика.Очень маленький образец размером 3 мм × 3 мм × 2 мм был вырезан в соответствии с требованиями к размеру оборудования. Морфологию наполнителей, их распределение и состояние границы раздела в композитах наблюдали с помощью сканирующего электронного микроскопа Tescan Lyra 3 (FESEM, Tescan, Брно, Чешская Республика). Порошки и изломанные поверхности для микроскопии покрывают золотом с использованием устройства для нанесения покрытия распылением в течение 20 с, и FESEM работает в режиме BSE при 20 кВ для всех композитных образцов.

4. Результаты и обсуждение

Сначала представлены результаты расчетов для анализа и прогнозирования свойств с различными комбинациями потенциальных полимеров и наполнителей для разработки новых TIM.Цель состоит в том, чтобы выяснить влияние внутренних свойств и атрибутов отдельных фаз в получаемых композитах. Затем методы определения характеристик и измерения свойств используются для подтверждения прогнозов в различных условиях. Результаты представлены здесь для разработки многообещающих эталонных TIM. Для разработки наилучших комбинаций наполнителей и матриц целевые значения свойств устанавливаются на основе требований появляющихся ТИМов. Теплопроводность в диапазоне от 1 до 2 Вт · м ^-1 K ^-1 считается типичным желаемым значением [3] для ТИМ на полимерной основе и, следовательно, значением 1.5 Вт · м ⁻¹ K ⁻¹ устанавливается в качестве порогового значения. Пороговые значения для получения желаемых структурных свойств для TIM определяются на основе свойств материала, взятых из литературы. Максимальное значение модуля сдвига в диапазоне от 0,5 до 0,6 ГПа и минимальное значение CTE менее 100 K ^-1 считаются целевыми значениями в расчетном дизайне для достижения комбинации наполнитель-матрица для удовлетворения структурных свойств предполагаемые TIM.

4.1. Прогноз минимального размера наполнителя

Автор и его сотрудники ранее сообщали [22,29], что размер частиц и сопротивление термической границы раздела между матрицей и наполнителем являются доминирующими и наиболее чувствительными параметрами при управлении эффективной теплопроводностью. конкретного полимерного композита с одним или гибридным наполнителем. Эти два параметра играют важную роль в управлении эффективной теплопроводностью композита через безразмерный параметр α _k , как определено в уравнении (11), также называемый эффектом радиуса Каптизы, где радиус частицы ( a _k ) – параметр принятия решения.Определяется максимально допустимое соотношение термического сопротивления границы раздела и радиуса частицы ( R _int / a _k ), по которому определяется минимальный размер наполнителя. Это зависит от собственной теплопроводности полимерной матрицы и наполнителя. После определения минимального размера частиц изучается влияние загрузки наполнителя для достижения целевых свойств предполагаемых композитов.

Две различные комбинации матриц и наполнителей с наименьшими и наибольшими значениями собственной теплопроводности используются для прогнозирования целевой эффективной теплопроводности композитов как функции объемной нагрузки при различных R _int / a _k соотношения.показывает изменение теплопроводности для этих двух комбинаций. Композитная система с полипропиленом в качестве матрицы и сферическим Al ₂ O ₃ в качестве наполнителя используется с учетом их самой низкой собственной теплопроводности (а), в то время как HDPE, нагруженный сферическим алмазом, рассматривается как вторая комбинация из-за самой высокой теплопроводности. значения (b) для определения порогового размера частиц. Как показано, начало увеличения эффективной теплопроводности предсказывается при максимальном отношении, равном единице в обоих случаях, т.е.е., R _int / a _k = 1. По прогнозам, значение R _int / a _k = 0,1 приведет к значительному увеличению эффективной теплопроводности, поскольку по сравнению с первозданной полимерной матрицей.

Прогнозируемая эффективная теплопроводность с учетом комбинаций самой низкой и самой высокой собственной теплопроводности матриц и наполнителей с различными соотношениями R _int / a _k .( a ) PP со сферическими наполнителями Al ₂ O ₃ . ( b ) HDPE со сферическими алмазными частицами.

Значение R _int для конкретной композитной системы зависит от внутренних свойств матрицы, таких как удельная теплоемкость, плотность и дебаевская скорость, а также от свойств, зависящих от границы раздела, таких как акустический импеданс и критический угол для фонона-фонона. связь. Для полимеров, имеющих меньшую насыпную плотность и большую теплоемкость, значение R _int обычно определяется из отношения скоростей фононов матрицы и наполнителей.На основе фононных скоростей керамики (например, AlN и Al ₂ O ₃ ) и полимеров (например, HDPE и PP) ожидается максимальное изменение R _int для композитных систем керамика-полимер. находиться в диапазоне от 1,15 × 10 ⁻⁷ до 22,5 × 10 ⁻⁷ м ² кВт ⁻¹ [30]. Сообщенные значения R _int в основном основаны на калибровке теоретических моделей с эмпирическими данными, поскольку точные скорости фононов редко доступны.В данной работе принимается значение 3,32 × 10 ⁻⁷ м ² K Вт ⁻¹ , которое приводится для аналогичной композитной системы с учетом обработки поверхности наполнителей в текущей экспериментальной работе. Это приводит к минимально необходимому радиусу частицы 3 мкм на основе R _int / a _k = 0,1.

4.2. Влияние комбинаций полимер-наполнитель на эффективную теплопроводность

Влияние потенциальных наполнителей, загруженных в полимеры-кандидаты (как показано на рисунке), на эффективную теплопроводность получаемых композитных систем изучается на основе установленного минимального размера частиц.a – f показывает прогнозируемое изменение теплопроводности в зависимости от объемной доли выбранных наполнителей в шести типах полимерных матриц в качестве потенциальных TIM. Обратите внимание, что увеличение содержания наполнителей в любой конкретной полимерной матрице имеет тенденцию к увеличению эффективной теплопроводности независимо от типа наполнителя, несмотря на широкий диапазон значений их собственной теплопроводности. Эффективная теплопроводность в основном определяется полимером (проводящей фазой), поэтому можно использовать любой керамический или углеродный наполнитель.Это связано с очень большой разницей значений теплопроводности непрерывной (полимер) и прерывистой (наполнитель) фазы.

Прогнозируемая эффективная теплопроводность композитов с различными комбинациями полимер – наполнитель при R _int / a _k = 0,1.

Из этого очевидно, что HDPE является наиболее подходящим полимером среди доступных кандидатов, где минимальная загрузка наполнителя в 35 об.% Является достаточной для достижения целевой теплопроводности, равной 1.5 Вт м ⁻¹ K ⁻¹ . Сверхвысокая теплопроводность 5 Вт · м ⁻¹ K ⁻¹ возможна в ТИМах на основе HDPE при увеличении загрузки наполнителей до 60 об.%. Следующими лучшими кандидатами в полимеры являются PSU и TPU, у которых прогнозируется теплопроводность ~ 3 Вт · м ^-1 K ^-1 при загрузке наполнителя ~ 60 об.%. Целевое пороговое значение 1,5 Вт · м ⁻¹ K ⁻¹ возможно при содержании наполнителя в этих двух полимерах ~ 45 об.%.Также очевидно, что обычно используемые композиты на основе эпоксидной смолы и силикона в качестве ТИМов ограничены максимальным значением ~ 2 Вт · м ^-1 K ^-1 даже при очень высокой загрузке ~ 50 об.% Из-за их низкая собственная теплопроводность. В полипропилене требуется очень высокая концентрация наполнителей для достижения пороговой эффективной теплопроводности до тех пор, пока не будет использован больший размер частиц и / или высокое соотношение сторон, что подтверждается в разделе валидации. Обратите внимание, что атрибуты наполнителя, такие как больший размер частиц, высокое соотношение размеров и / или гибридные наполнители, могут использоваться для уменьшения требуемой объемной доли для достижения любой конкретной теплопроводности [29,31], и, таким образом, возможна дальнейшая оптимизация конструкции.Помимо теплового отклика, обратите внимание, что другие требования, такие как механическая податливость и диэлектрические характеристики TIM, не должны нарушаться только из-за достижения высокой теплопроводности. Следовательно, необходимы дальнейшие исследования для сравнения комбинаций полимер-наполнитель на основе механических свойств, которые обсуждаются далее.

4.3. Влияние комбинаций полимер-наполнитель на эффективный модуль сдвига и коэффициент теплового расширения

ТИМ, изготовленные из полимерных композитов, должны демонстрировать хорошую механическую податливость, ведущую к заполнению пустот при установке между модулями с низким КТР в электронных корпусах.Это приводит к наиболее фундаментальным инженерным требованиям, а именно: (1) низкий модуль сдвига, позволяющий изменять форму и улучшенную адгезию, и (2) более низкий КТР, чтобы минимизировать несоответствие КТР чипам и теплораспределителям в корпусе, чтобы избежать термосмеханических стрессы. Поэтому влияние выбранных наполнителей, загруженных в потенциальные полимеры, на эффективные G и CTE изучается как функция объемной доли. и показывают эффективные G и CTE как функцию объемной доли выбранных наполнителей в потенциальных полимерных матрицах, соответственно.Из этого видно, что TPU и силикон сохраняют свои низкие значения G, несмотря на добавление очень высокой нагрузки любого типа наполнителя, что связано с очень низким внутренним значением G этих матриц. Однако их относительно более высокий КТР, особенно в случае силикона, имеет тенденцию быть ограничивающим фактором, как показано на рис. Чтобы удовлетворить требованию достижения заданного значения КТР <100 × 10 ^-6 K ^-1 , потребуется очень высокая загрузка (> 50 об.%) Наполнителя в силиконе. Напротив, значение G имеет тенденцию к увеличению в зависимости от объемной доли наполнителя, когда эпоксидная смола, PSU и PP используются в качестве матрицы.Следовательно, предполагаемый композит TIM не сможет поддерживать требуемое максимальное значение 0,5–0,6 ГПа в таких условиях. Эта тенденция к увеличению G относительно меньше в случае наполнителей BN и графита по сравнению с другими наполнителями, что связано с их небольшими внутренними значениями G. Тем не менее, относительно низкие собственные значения CTE, особенно для блоков питания и эпоксидной смолы, являются одними из привлекательных вариантов для использования в качестве TIM. Как показано на фиг.3, эффективный КТР композитов в случае эпоксидной смолы и блока питания имеет тенденцию к снижению, что, как ожидается, приведет к снижению термических напряжений из-за меньшего несоответствия с соседними модулями.Среди всех потенциальных полимеров-кандидатов HDPE, по прогнозам, будет лучшим кандидатом для достижения желаемых CTE и G при загрузке наполнителями с минимум 30 об.% И максимум 45 об.%. Следовательно, существует компромисс между достижением сверхвысокой теплопроводности и поддержанием низкого значения модуля, когда концентрация наполнителя в HDPE превышает 40%.

Прогнозируемый эффективный модуль сдвига композитов с различными комбинациями полимер-наполнитель.

Прогнозируемый эффективный коэффициент теплового расширения композитов с различными комбинациями полимер – наполнитель.

Вышеупомянутое расследование приводит к некоторым важным выводам, которые считаются важными для разработчиков TIM. Эффективные термические и структурные свойства в основном зависят от фазы непрерывной полимерной матрицы, в то время как большинство наполнителей оказывают аналогичное влияние на эффективные свойства. КТР перечисленных полимеров значительно выше по сравнению с потенциальными наполнителями, в то время как в случае G справедливо обратное. деформация локализована в полимерной матрице.В таких ситуациях, как сообщалось ранее [29], основным механизмом упрочнения является ограничение движения молекулярных цепей полимера на межфазной границе с наполнителями, что требует достаточно хорошей межфазной прочности. Что касается выбора наполнителя, решение может быть дополнительно принято на основании других критериев, таких как стоимость, доступность и, что наиболее важно, электрические свойства, аналогичные полимерной матрице, для достижения высокой прочности на пробой в полученных композитах.

4.4. Микроскопический анализ наполнителей и синтезированных композитов

Для подтверждения предсказаний модели разработаны полимерные композиты с наполнителем с низким и большим объемом с использованием различных матриц и атрибутов наполнителя в соответствии с прогнозами. показывает детали этих образцов. показаны некоторые репрезентативные изображения FESEM композитов HDPE с Al ₂ O ₃ и AlN в качестве наполнителей при различных нагрузках и размерах, а также показаны изображения PP, загруженного Al ₂ O ₃ и AlN.Изображения порошков A ₂ O ₃ и AlN, как показано, соответствуют указанным размерам и формам. Более крупные частицы Al ₂ O ₃ размером 45 мкм примерно равноосны, в то время как частицы Al ₂ O ₃ размером 15 мкм в основном сплюснуты с большим аспектным отношением. Режим обратного рассеяния электронов (BSE) используется для захвата изображений композитов для достижения лучшего контраста наполнителей в матрицах. В целом пористость не наблюдается, а частицы равномерно распределены в матрицах, что показывает эффективность технологического маршрута, использованного в данной работе.Цветные изображения BSE позволяют идентифицировать керамические частицы в матрице. Благодаря более высокому среднему атомному весу керамических частиц они выглядят ярче по сравнению с полимерной матрицей. Контурные изображения этих изображений дополнительно проясняют наличие наполнителей в матрице, которая выглядит зеленовато-красной в синеватой матрице из-за более высокой плотности сигнала.

Характеристика керамических наполнителей и трещиноватых композитов на основе полиэтилена высокой плотности. Изображения FESEM HDPE / керамического композита при ( a ) 30 об.% AlN (15 мкм), ( b ) 35 об.% Al ₂ O ₃ (15 мкм) нагрузке и ( c ) ) 20 об.% Al ₂ O ₃ (45 мкм) загрузка.

Характеристика трещиноватых композитов на основе полипропилена. Изображения FESEM ПП / керамического композита при ( a ) 10 об.% AlN (5 мкм), ( b ) 30 об.% Al ₂ O ₃ (15 мкм) нагрузке и ( c ) ) Загрузка 50 об.% AlN (5 мкм).

Таблица 2

Описание полученных образцов полимерных композиционных материалов.

905

Матрица	Наполнители	Средний размер частиц (мкм)	Состав, φ (об.%)
HDPE	9011 9011 9011 905 905 905 31	10, 20, 35, 50
HDPE	Al 2 O 3	45	10, 20, 35, 50
PP	AlN	2	5	5, 10, 15, 20, 30, 40, 50
PP	AlN	15	10, 20, 35, 50
PP	Al 2 O 3	15	10, 30, 50
HDPE	AlN	15	10, 30
TPU	AlN	5	20, TP 25	905 О 3	5	20, 25

4.5. Проверка расчетного дизайна

a – f показывает измеренную и прогнозируемую теплопроводность как функцию загрузки наполнителей от низкой до очень высокой концентрации в различных композитных системах с разными характеристиками. Эти композитные системы включают несколько комбинаций HDPE, TPU и PP в качестве матрицы с Al ₂ O ₃ и AlN в качестве наполнителей с различными размерами частиц, как описано в. Сравнение измеренной и прогнозируемой теплопроводности, в целом, подтверждает, что предложенный метод дифференциальной эффективной среды достаточно точен для прогнозирования теплового отклика полимерных композитов для предполагаемого TIM.Это связано с тем фактом, что взаимодействия между эффективными полями соседних частиц хорошо фиксируются текущей моделью благодаря интеграции бесконечно разбавленных добавок наполнителей в однородные матрицы. Таким образом, результаты показывают, что предложенная модель без разбавления преодолела недостатки, типичные для теории разбавления эффективной среды, которые недооценивают теплопроводность, особенно при более высокой загрузке наполнителя.

Измеренная и прогнозируемая теплопроводность различных типов наполнителей и матричных композитов в зависимости от загрузки наполнителя.( a ) HDPE / Al ₂ O ₃ композиты с 15 мкм Al ₂ O ₃ . ( b ) HDPE / Al ₂ O ₃ композитов с 45 мкм Al ₂ O ₃ . ( c ) Композиты HDPE / AlN с 15 мкм AlN. ( d ) ТПУ с AlN и Al ₂ O ₃ композитов с наполнителем 5 мкм. ( e ) Композиты PP / AlN с 5 мкм AlN. ( f ) PP / Al ₂ O ₃ композитов с 15 мкм Al ₂ O ₃ .

Как показано в а – с, композиты на основе полиэтилена высокой плотности, содержащие Al ₂ O ₃ (размеры: 15 мкм и 45 мкм) и AlN (размер: 15 мкм), демонстрируют более высокую теплопроводность для любой конкретной объемной доли наполнителя. , а проводимость увеличивается с увеличением содержания наполнителя. Напротив, композиты на основе TPU с 5 мкм Al ₂ O ₃ и AlN каждый (d) и композиты на основе PP, содержащие 5 мкм и 15 мкм Al ₂ O ₃ (e, f) , приводят к относительно более низкой теплопроводности по сравнению с композитами на основе HDPE из-за меньшей собственной теплопроводности TPU и PP (непрерывная фаза), как обсуждалось ранее.Влияние размера наполнителя на результирующую теплопроводность также можно понять, если мы сравним мелкие и большие размеры частиц в композитных системах HDPE-Al ₂ O ₃ с двумя разными размерами. Например, композиты HDPE / 45 мкм-Al ₂ O ₃ могут обеспечить более высокую теплопроводность по сравнению с композитами HDPE / 15 мкм-Al ₂ O ₃ для любой конкретной загрузки наполнителя. Обратите внимание, что из d те композиты на основе ТПУ, содержащие 5 мкм Al ₂ O ₃ и AlN, дают почти одинаковую проводимость, что подтверждает, что собственная теплопроводность непрерывной полимерной матрицы играет доминирующую роль в контроле эффективной теплопроводности.Другим важным фактором является соотношение сторон частицы при регулировании эффективной теплопроводности при сравнении композитной системы PP / 5 мкм-AlN (равноосной / почти сферической) с PP / 15 мкм-Al ₂ O ₃ (сплюснутый), как показано на e, f соответственно. Из результатов можно заключить, что относительное увеличение эффективной теплопроводности в случае частицы сплюснутой формы больше, чем у сферической. Это связано с тем фактом, что сплюснутые (или вытянутые) частицы имеют большую тенденцию к образованию взаимосвязанной сети и, следовательно, могут обеспечивать более высокую эффективную теплопроводность, что демонстрируется с помощью уравнения (9).

Как следует из приведенных выше результатов, размер наполнителя и соотношение сторон напрямую влияют на общие тепловые характеристики TIM. Следовательно, эти свойства наполнителя следует выбирать осторожно, чтобы не ухудшить механические характеристики TIM. Большой наполнитель может привести к плохой адгезии с прикрепленными электронными модулями, что приведет к образованию пустот. С другой стороны, очень маленькие наполнители, такие как наночастицы, могут привести к значительному увеличению сопротивления Капице из-за большей площади поверхности и увеличения граничного рассеяния, что приводит к затруднению теплопередачи и, таким образом, к снижению теплопроводности ТИМ, как продемонстрировано измерениями и прогнозами.Также установлено, что эффект сопротивления Капице может быть уменьшен, если использовать наполнитель с высоким коэффициентом формы при одинаковой процентной загрузке.

Для подтверждения теплопроводности подготовленных композитов проводится тепловидение с помощью инфракрасной камеры. Тепловые изображения HDPE / Al ₂ O ₃ (45 мкм Al ₂ O ₃ ) композитов PP / AlN (15 мкм AlN) с загрузкой 10, 20, 35 и 50 об.%, Полученные как функция времени показано в.Как правило, композиты с более высокой нагрузкой имеют тенденцию увеличивать теплопередачу с более высокой температурой с более высокой скоростью. Композит HDPE, содержащий 45 мкм Al ₂ O ₃ , показывает значительно большее повышение температуры по сравнению с композитом PP с 15 мкм AlN при любой конкретной нагрузке и времени. Этот качественный анализ согласуется с измеренной и прогнозируемой теплопроводностью этих композитных систем и подтверждает, что полимерная матрица как непрерывная фаза с большим размером частиц является доминирующим фактором при регулировании эффективной теплопроводности.

Тепловизионные изображения различных композитов, полученные в зависимости от времени. Композиты HDPE / Al ₂ O ₃ (45 мкм Al ₂ O ₃ ) с нагрузкой 10, 20, 35 и 50 об.%. Композиты PP / AlN (15 мкм AlN) с загрузкой 10, 20, 35 и 50 об.%.

Сравнение измеренного и прогнозируемого КТР композитов TPU, нагруженных AlN и Al ₂ O ₃ , в зависимости от объемной доли показано на a. Соответствующие FESME-изображения ТПУ с 20 об.% Al ₂ O ₃ и наполнителями AlN также показаны на b, c соответственно, что подтверждает отсутствие дефектов в полученных композитах.Можно заметить, что керамические частицы имеют немного высокое соотношение размеров и почти однородно диспергированы в полимерной матрице. Прогнозы КТР находятся в хорошем согласии с экспериментально измеренными значениями, и можно заметить, что КТР композита может быть адаптирован путем подходящей загрузки керамических наполнителей с низким КТР. Добавление керамических наполнителей в полимерную матрицу имеет тенденцию к снижению эффективного КТР по мере увеличения объемной доли и, таким образом, имеет потенциал для уменьшения несоответствия с соседними модулями в электронных корпусах, что является одним из требований высокопроизводительных TIM.Обратите внимание, что небольшая разница между прогнозируемым и измеренным значением связана с тем фактом, что модель, используемая в текущей работе, основана на подходе среднего поля, который предполагает случайное распределение сферических наполнителей в матрице.

( a ) Прогноз эффективного CTE композитов TPU / Al ₂ O ₃ и TPU / AlN в зависимости от нагрузки наполнителя. Также показаны измеренные значения КТР этих композитных систем с нагрузками 20 об.% И 25 об.%.( b ) FESEM-изображения TPU / Al ₂ O ₃ 20 об.% AlN (5 мкм). ( c ) Изображения FESEM загрузки TPU / AlN 20 об.% AlN (5 мкм).

4.6. Влияние границы раздела наполнитель-матрица и ориентации наполнителя

Как было продемонстрировано, наполнители с более высокой теплопроводностью приводят к требуемой повышенной теплопроводности ТИМ, но имеют некоторые недостатки с точки зрения механических свойств, преимущественно при более высокой нагрузке. Следовательно, для разработки новых ТИМ желательно достижение тех же тепловых характеристик при более низкой загрузке наполнителя.Изучаются такие методы, как повышение термической совместимости на границе раздела наполнитель-матрица и выравнивание наполнителя. Помимо комбинации наполнитель-матрица, размера и дисперсии наполнителя, текущая вычислительная структура может учитывать ориентацию наполнителя и влияние границы раздела наполнитель-матрица на результирующую эффективную теплопроводность. Считается, что некоторые представительные опубликованные работы подтверждают модель и предоставляют некоторые руководящие принципы для новых полимерных ТИМов.

Суть нынешней модели состоит в том, чтобы минимизировать порог перколяции для достижения максимальной теплопроводности за счет адаптации таких факторов, как размер частиц, соотношение сторон и предпочтительная ориентация наполнителя, в дополнение к внутренним свойствам наполнителей и матриц.С этой целью модель подтверждается экспериментальными данными теплопроводности с различными случаями сопротивления границы раздела наполнитель – матрица ( R _int ) и ориентацией наполнителя (⟨cos2θ⟩), доступными в литературе [32,33,34 ]. Сравнение представленных экспериментальных результатов с текущей моделью представлено в, чтобы продемонстрировать способность модели учитывать эти факторы в результирующей эффективной теплопроводности для различных комбинаций наполнитель-полимер. Соответствующие используемые входные данные приведены в.Deng et al. [34] исследовали композиты с полифениленсульфидом (PPS) в качестве матрицы и расширяющимся графитом (EG) в качестве наполнителя, что продемонстрировало очень низкий уровень R _int из-за сильного взаимодействия PPS и EG, как показано на . Moradi et al. [32], с другой стороны, показали высокое термическое сопротивление между наполнителями из гексагонального нитрида бора (hBN) при загрузке в эпоксидную матрицу, как показано на b. Тем не менее, больший размер частиц (180 мкм) по сравнению с меньшим размером наполнителя (30 мкм) hBN привел к более высокой эффективной теплопроводности, что подтверждает, что межфазное сопротивление может быть компенсировано за счет использования частиц большего размера.

Проверка текущей модели с использованием экспериментально измеренных результатов теплопроводности для различных случаев термического сопротивления границы раздела и ориентации наполнителей.

Таблица 3

Параметры, используемые в модели для проверки влияния границы раздела наполнитель-матрица и ориентации наполнителя.

Температурное сопротивление внутр
(м ² кВт ^{– 1} ) 905 905 ]

Теплопроводность наполнителя, λ p (Вт м −1 K −1 )	Теплопроводность матрицы, λ м 98 (Вт · м 9 −1 K −1 )	Радиус частицы, r 1 (мкм)	Соотношение сторон, ξ	Влияние ориентации cos2θ3	Арт.
200	0,24	2,5	0,05	1/3	1 × 10 −7	[34]
600	0,12	1/3	23 × 10 −7	[32]
600	0,14	5	0,095	1/3	23 × 10 −7
600	0.24	8	0,2	1	16,6 × 10 −7	[33]
600	0,24	8	0,2	0 −		[33]

Выравнивание наполнителей в полимерной матрице для формирования непрерывных теплопроводящих путей в последнее время стало целью многих исследователей, что могло бы привести к прорыву в разработке эффективных и надежных TIM. c, d демонстрирует подтверждение существующей структуры с экспериментальной работой Yu et al.[33], которые продемонстрировали индуцированное процессом выравнивание в плоскости и через плоскость частиц hBN в матрице TPU. Измеренная теплопроводность композитов в двух различных ориентациях очень хорошо согласуется с прогнозами текущей модели, что подтверждает способность текущей модели включать ориентацию наполнителя в дополнение к другим атрибутам. Показано, что наполнители с параллельным выравниванием могут привести к чрезвычайно высокой теплопроводности по сравнению с невыровненными наполнителями.

Ключевые свойства огнеупорных материалов: понимание теплопроводности, прочности на сжатие и пористости

Список литературы

1 M. H. Van de Voorde и G. W. Meetham, Огнеупоры и изоляционные материалы , in: Materials for High Temperature Engineering Applications, Springer, Heidelberg, 2000

2 Огнеупорные и изоляционные материалы, в: Эффективное использование энергии (2-е изд.) , И. Г. К. Драйден (редактор), Баттерворт, Лондон, 1982

3 Огнеупорные материалы; Карманное руководство: Дизайн, свойства, тестирование, G. Routschka (ed), Vulkan-Verlag, Essen, 2008

4 Р. Р. Миллер et al. , J. Chem. Англ. Данные , 1962 , 7, 251

5 Наценко А.И. и др. ., Refractroes , 1983 , 24, 215

6 Л. Э. Монг, Упругое поведение и ползучесть огнеупорных кирпичей при растягивающих и сжимающих нагрузках, Министерство торговли США, Вашингтон, округ Колумбия, 1946 г.

7 м.Х. Рахман и др. , Процедуры Eng. , 2015 , 105, 121

8 Y. Li et al. , Эксперименты по механическим характеристикам набивного материала пода доменной печи и огнеупорного раствора из углеродного кирпича на 2-й Международной конференции по разработке материалов и их применению, , Шанхай, 2015 г.

9 K. Kasoya et al., J. Phys. Chem. Ref. Данные, 1985 , 14, 947

10 р.Cromarty et al., J. S. Afr. Inst. Мин. Металл ., 2014 , 114, 4

11 S. Aminorroya et al. , Оценка основного порошка промежуточного ковша для непрерывного литья чистой стали , в AIS Tech – Конференция и выставка по технологиям чугуна и стали , Кливленд, 2006 г.

12 M. Kalantar et al., J. Mater. Англ. Perf. , 2010 , 19, 237

13 С. Далквист и Т. Гутовски, Анализ жизненного цикла традиционных производственных технологий: литье в песчаные формы в 2004 ASME Международный конгресс и выставка машиностроения , 2004, Анахайм, США

14 г.Р. Юснер и Дж. Т. Шапланд, Проницаемость огнеупоров для доменных печей в Шестнадцатое совещание Американского керамического общества , Питтсбург, 1958 г.

Что такое теплопроводность? – Определение и уравнение

Факторы влияния и уравнение

Прежде чем исследовать уравнение теплопроводности, нам необходимо понять влияющие переменные. Тепло обычно обозначается буквой Q. Теперь, когда площадь (обозначенная «А») поверхности увеличивается, увеличивается и количество прошедшего через нее тепла, которое также необходимо учитывать в уравнении.Но как сравнивать разные значения тепла, не зная, как быстро происходит передача? Если бы нам пришлось разделить передаваемое тепло на время («t»), мы бы пришли к скорости теплопроводности, которая была бы «Q / t», более точной мерой того, насколько быстро происходит теплопередача.

Но это все? Из нашего обсуждения выше мы знаем, что теплопередача (Q) не могла бы происходить без разницы в температуре или, с научной точки зрения, разницы температур (Hot temp. – Cold Temp.). Расстояние между поверхностями также имеет значение, в зависимости от того, насколько хорошо объект проводит тепло. Чем дальше друг от друга поверхности, тем на большем расстоянии внутренние молекулы должны обмениваться энергией, чтобы тепло передавалось от одной поверхности к другой.

Кстати, как мы можем учесть различную проводимость различных материалов, таких как ткань для дивана и металлы? Мы делаем это, используя константу материала «K», известную как константа теплопроводности , которая определяется экспериментально для каждого материала.Теперь, когда мы учли все факторы, мы можем сказать по их влиянию на теплопередачу и взаимосвязи с ними, что уравнение выглядит следующим образом:

Уравнение теплопроводности (K)

Хотя на теплопроводность также влияют конвекция и фазовые переходы (переходы из / в твердые тела, жидкости и газы), здесь мы в основном имели дело с твердыми телами. Обратная величина теплопроводности известна как удельное тепловое сопротивление , которое является мерой того, насколько хорошо материал препятствует прохождению электрического тока .Это очень полезная цифра, которую нужно знать при выборе изоляторов, таких как резиновые кожухи для электрических проводов, или, скажем, ношение толстых резиновых сапог при работе с электричеством, если электричество случайно не коснется вас.

Краткое содержание урока

Тепло – это форма энергии. Чем выше средняя кинетическая энергия молекул внутри объекта, тем выше его температура. Разница температур является основой теплопередачи, при которой энергия перетекает от более горячего тела к более холодному. Теплообмен может происходить тремя способами: теплопроводностью, , конвекцией, и излучением , ; иногда все одновременно. Когда мы упоминаем теплопроводность , мы имеем в виду способность материала передавать тепло . Константа теплопроводности для каждого материала разная и определяется экспериментально.

Они открывают новый неорганический материал с самой низкой теплопроводностью

Science Newsroom, 15 июля (EFE).- Примерно 70% всей энергии, производимой в мире, теряется в виде тепла, поэтому материалы с низкой теплопроводностью имеют важное значение. Теперь группа ученых открыла новый неорганический материал с самой низкой когда-либо зарегистрированной теплопроводностью.

Это открытие открывает путь к разработке новых термоэлектрических материалов, которые необходимы для устойчивого общества, говорят ученые из Ливерпульского университета.

Исследование опубликовано в журнале Science и предоставляет важные новые знания об управлении энергопотреблением.По мнению авторов, «это ускорит разработку новых материалов для преобразования отработанного тепла в энергию и для эффективного использования топлива».

Он также представляет собой большой прогресс в управлении тепловым потоком в атомном масштабе, достигнутый благодаря дизайну материалов, – говорится в примечании Британского университета.

Команда, возглавляемая Мэттом Россейнски и Джоном Аларией, разработала и синтезировала новый материал таким образом, чтобы объединить два различных расположения атомов, которые, как было обнаружено, уменьшают скорость распространения тепла через структуру твердого тела.

Этот новый материал, объединенный в две структуры, имеет гораздо более низкую теплопроводность, чем любой из исходных материалов с одной структурой, что ученые называют неожиданным.

Если принять теплопроводность стали за 1, то титановый стержень равен 0,1, вода и строительный кирпич – 0,01, новый материал – 0,001, а воздух – 0,0005.

Примерно 70% всей вырабатываемой в мире энергии тратится в виде тепла, и разработка новых и более эффективных термоэлектрических материалов, способных преобразовывать тепло в электричество, считается ключевым источником чистой энергии.

«Обнаруженный нами материал имеет самую низкую теплопроводность среди всех неорганических твердых тел и почти так же плохо проводит тепло, как и сам воздух», – говорит Россейнски.

Статья Источник

Заявление об ограничении ответственности: эта статья создана на основе фида и не редактируется нашей командой.

Углеродно-волокнистый композит обеспечивает металлопроводность

Toray Industries Inc., Япония.разработала технологию теплопроводности, которая повышает теплоотдачу пластика, армированного углеродным волокном (CFRP), до свойств металлов. Применение этой технологии к углепластику эффективно рассеивает тепло от его источников через пути теплопроводности внутри материала. Это помогает предотвратить деградацию батареи в мобильных приложениях, одновременно повышая производительность электронных устройств.

Обычно этот легкий, прочный и жесткий пластик используется в самолетах, автомобилях, компонентах инфраструктуры, спортивных товарах и электронных устройствах.Повышение теплоотдачи углепластика при его использовании в качестве конструкционного материала в условиях повышенной мобильности важно для предотвращения износа аккумуляторов из-за тепловыделения во время зарядки. Однако углепластик менее теплопроводен, чем алюминиевые сплавы и другие металлы, что требует усилий по увеличению теплоотвода за счет использования внешних или внутренних листов графита. Однако эти листы легко ломаются, рассыпаются и повреждаются, что ухудшает характеристики углепластика.

На протяжении многих лет Toray использовала запатентованную технологию для разработки и применения жесткого пористого углепластика, образующего трехмерные сети с короткими углеродными волокнами.В этом случае Toray создал теплопроводный слой, используя пористую основу из углепластика, которая защищает графитовые листы. Ламинирование препрега из углепластика на этот теплопроводящий слой позволяет Toray достичь теплопроводности выше, чем у металлов. Это было бы невозможно с обычным углепластиком без ущерба для механических свойств и качества материала.

Препрег – это листовой промежуточный материал, изготовленный путем пропитки волокон смолой для их усиления. Обычно используются в фюзеляжах самолетов, главном и хвостовом крыльях, а также в других основных конструктивных элементах.Он также используется в стержнях клюшек для гольфа, удилищах, рамах теннисных ракеток и другом спортивном оборудовании.

Toray может изменять толщину и расположение слоев графитовых листов, которые образуют пути теплопроводности, тем самым обеспечивая гибкую конструкцию управления температурой, которая контролирует пути отвода или использования тепла для повышения эффективности охлаждения и рассеивания тепла из углепластика.

Прорыв

Toray – технологическое решение для эффективного отвода тепла от батарей и электронных схем без ущерба для легкости углепластика.Компания ожидает, что приложения из углепластика, использующие ее технологию, будут включать в себя передовую мобильность, мобильные электронные устройства и носимые устройства, требующие легкости и рассеивания тепла.

Теплопроводность в классических низкоразмерных решетках – Исследовательский портал Абердинского университета

@article {7d2809b2d95e40829c24d251a7e3102e,

title = “Теплопроводность в классических низкоразмерных решетках”,

аннотация = “Получение законов термодинамики необратимой термодинамики от простых микроскопических моделей – одна из задач неравновесной статистической механики.Мы рассматриваем стационарный перенос энергии в кристаллах на основе простых математических моделей, состоящих из связанных осцилляторов на решетке. Обсуждается роль размерности решетки в нарушении закона Фурье и подчеркиваются некоторые универсальные количественные аспекты: дивергенция конечной теплопроводности характеризуется универсальными законами в одном и двух измерениях. Представлены методы равновесной и неравновесной молекулярной динамики, а также дан критический обзор предыдущих численных результатов.Аналитические результаты для неравновесной динамики могут быть получены в гармонической цепочке, где также можно понять роль беспорядка и локализации. Традиционный кинетический подход, основанный на уравнении Больцмана-Пайерлса, также кратко описан со ссылкой на одномерные цепи. Можно определить простые модели игрушек, в которых проводимость конечна. Кратко обсуждается аномальный перенос в интегрируемых нелинейных системах. Наконец, очерчиваются возможные темы будущих исследований. (C) 2002 Эльзевьер Сайенс Б.V. Все права защищены. »,

keywords =« теплопроводность, классические решетки, неравновесная молекулярная динамика, неупорядоченная гармоническая цепочка, двухатомная тода-решетка, теплопроводность, перенос энергии, статистическая механика, гамильтоновы системы, ангармонические цепочки.